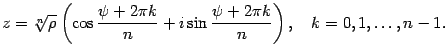- •Вопрос №1 Линейные дифференциальные уравнения второго порядка с переменными коэффицентами
- •Вопрос №2 Линейное дифференциальное уравнение с постоянными коэффициентами.
- •Вопрос№3 Линейное неоднородное дифференциальное уравнение (лнду) второго порядка с постоянными коэффициентами
- •Вопрос №6 Числовые ряды
- •Вопрос №7 Признак Даламбера .Радикальный признак Коши
- •Вопрос №8 Знакочередующиеся ряды: признак Лейбница
- •Вопрос №9 Знакопеременные ряды Знакопеременные ряды
- •Вопрос №10 Степенные ряды
- •Вопрос №11 Ряды Тейлора и Маклорена
- •Вопрос №12 Элементы гармонического анализа
- •Вопрос №13 разложение в ряд Фурье
- •Вопрос№14 Комплексные числа и действия над ними
- •Вопрос №15 Извлечение корня из комплексного числа
- •Вопрос №16 Понятие функции комплексного переменного
Вопрос №15 Извлечение корня из комплексного числа
Заголовок этого раздела является не совсем точным. Дело в том, что корень из ненулевого комплексного числа однозначно определить нельзя. Он всегда имеет столько значений, какова его степень. Поэтому в данном разделе мы будем говорить о решении уравнения
|
(17.14) |
где
неизвестным служит ![]() ,
а
,
а ![]() --
известное комплексное число. Но поскольку
в школе решение этого уравнения
записывалось в виде
--
известное комплексное число. Но поскольку
в школе решение этого уравнения
записывалось в виде ![]() ,
то, не слишком соблюдая математическую
строгость, можно говорить, что мы будем
извлекать корень
,
то, не слишком соблюдая математическую
строгость, можно говорить, что мы будем
извлекать корень ![]() -ой
степени из комплексного числа
.
Итак, решаем уравнение (17.14).
-ой
степени из комплексного числа
.
Итак, решаем уравнение (17.14).
Если ![]() ,
то
,
то ![]() .
Пусть
.
Пусть ![]() .
Запишем число
в
тригонометрической форме:
.
Запишем число
в
тригонометрической форме: ![]() .
Здесь
.
Здесь ![]() и
и ![]() --
известные величины. Запишем неизвестное
число
в
тригонометрической форме:
--
известные величины. Запишем неизвестное
число
в
тригонометрической форме: ![]() .
Здесь
.
Здесь ![]() и
и ![]() --
неизвестны. По формуле Муавра
--
неизвестны. По формуле Муавра
![]()
Таким образом,
![]()
Если
два комплексных числа равны, то их модули
должны быть равны. Поэтому ![]() .
В этом соотношении
и
--
положительные числа, следовательно
.
В этом соотношении
и
--
положительные числа, следовательно ![]() ,
где справа стоит обычный арифметический
корень из положительного числа.
,
где справа стоит обычный арифметический
корень из положительного числа.
Если
два комплексных числа равны, то аргументы
у них могут различаться только на
величину, кратную ![]() .
Поэтому
.
Поэтому ![]() ,
, ![]() .
Отсюда находим, что
.
Отсюда находим, что
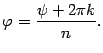
В итоге получили:
|
(17.15) |
Значения ![]() ,
отличные от указанных в этой формуле,
дадут те же значения
,
которые можно получить при
,
отличные от указанных в этой формуле,
дадут те же значения
,
которые можно получить при ![]()
Вопрос №16 Понятие функции комплексного переменного
Понятие функции комплексного переменного является частным случаем общего математического понятия функции.
Определение. Если
А – некоторое множество комплексных
чисел z (геометрически – множество
точек комплексной плоскости), и каждому
числу z![]() А
поставлено в соответствие по некоторому
закону число w
В
(где В – также множество комплексных
чисел), то говорят, что на множестве А
определена функция комплексного
переменного z (или
отображение множества А в В ).
А
поставлено в соответствие по некоторому
закону число w
В
(где В – также множество комплексных
чисел), то говорят, что на множестве А
определена функция комплексного
переменного z (или
отображение множества А в В ).
Записывают: w = f (z).
Множество А называют областью определения функции, В – множество, состоящее из значений, принимаемых функцией, называют областью значений функции.
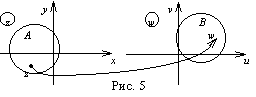 Принято
множества А и В,
изображать на отдельных комплексных
плоскостях (см. рис. 5): плоскость z комплексных
чисел z = х + i
у и
плоскость w комплексных чисел w = u + i
v .
Принято
множества А и В,
изображать на отдельных комплексных
плоскостях (см. рис. 5): плоскость z комплексных
чисел z = х + i
у и
плоскость w комплексных чисел w = u + i
v .
При этом точка w0 = f (z0) называется образом точки z0, а z0– прообразом точки w0.
В частности, если А расположено на действительной оси ох, то z = х является действительным переменным. Если же все значения w также действительны, то приходим к понятию функции действительного переменного как частному случаю функции комплексного переменного.
В общем случае z = х + i у, w = u (х, у) + i v (х, у).
Геометрически функцию f (z ) можно рассматривать как отображение множества А на множество В, переводящее точку (х, у) множества А в точку ( u, v ) множества В. Высказывание “ функция w = f (z) определена на множестве А” эквивалентно следующему: “ каждой точке (х, у) из А поставлены в соответствие действительные числа u и v ” . Иными словами, на множестве А определены две действительные функции
![]() и
и ![]() двух
действительных переменных х и у.
Итак, задание функции комплексного
переменного w = f (z)
равносильно заданию двух функций двух
действительных переменных
и
.
двух
действительных переменных х и у.
Итак, задание функции комплексного
переменного w = f (z)
равносильно заданию двух функций двух
действительных переменных
и
.
Например, соотношение w = z2 = (x +iy)2 = x2 – y2 + i2xy эквивалентно следующим: u = x2 – y2, v = 2xy.