Вопрос №1 Линейные дифференциальные уравнения второго порядка с переменными коэффицентами

Линейное однородное уравнение второго порядка с переменными коэффициентами записывается в виде

где a₁(x) и a₂(x) являются непрерывными функциями на отрезке [a,b].

Линейная независимость функций. Определитель Вронского

Функции y₁(x), y₂(x), ..., y_n(x) называются линейно зависимыми на отрезке [a,b], если существуют постоянныеα₁, α₂, ..., α_n, одновременное не равные нулю, такие, что для всех значений x из этого отрезка справедливо тождество

Если же это тождество выполняется лишь при α₁ = α₁ = ... = α_n = 0, то указанные функции y₁(x), y₂(x), ..., y_n(x)называются линейно независимыми на отрезке [a,b].  Для случая двух функций критерий линейной независимости можно записать в более простом виде: Функцииy₁(x), y₂(x) будут линейно независимыми на отрезке [a,b], если их отношение на данном отрезке тождественно не равно постоянной:

В противном случае, при  , эти функции будут линейно зависимыми.  Пусть n функций y₁(x), y₂(x), ..., y_n(x) имеют производные (n − 1) порядка. Определитель

называется определителем Вронского или вронскианом для указанной системы функций.  Теорема. Если система функций y₁(x), y₂(x), ..., y_n(x) линейна зависима на отрезке [a,b], то ее определитель Вронского тождественно равен нулю на этом отрезке.  Отсюда следует, что если определитель отличен от нуля хотя бы в одной точке отрезка [a,b], то функции y₁(x),y₂(x), ..., y_n(x) будут линейно независимыми. Это свойство определителя Вронского позволяет выяснить, являются ли найденные решения однородного дифференциального уравнения линейно независимыми.

Вопрос №2 Линейное дифференциальное уравнение с постоянными коэффициентами.

Линейное дифференциальное уравнение с постоянными коэффициентами — обыкновенное дифференциальное уравнение вида:

где

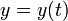•  — искомая функция,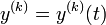

•  — её 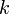 -тая производная,

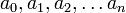•  — фиксированные числа,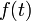

•  — заданная функция (когда 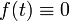 , имеем линейное однородное уравнение, иначе — линейное неоднородное уравнение).

• Уравнение Коши — Эйлера является частным случаем линейного дифференциального уравнения вида:

• ,

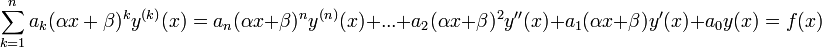• приводимым к линейному дифференциальному уравнению с постоянными коэффициентами подстановкой вида  .

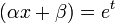Вопрос№3 Линейное неоднородное дифференциальное уравнение (лнду) второго порядка с постоянными коэффициентами

Линейное неоднородное дифференциальное уравнение (ЛНДУ) второго порядка с постоянными коэффициентами имеет вид  , где p иq – произвольные действительные числа, а функция f(x) – непрерывна на интервале интегрирования X. Сформулируем теорему, которая показывает в каком виде искать общее решение ЛНДУ. Общее решение на интервале X линейного неоднородного дифференциального уравнения   с непрерывными на интервале интегрирования X коэффициентами   и непрерывной функцией f(x) равно сумме общего решения  соответствующего ЛОДУ и какого-нибудь частного решения   исходного неоднородного уравнения. То есть,  . Таким образом, общим решением линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами является сумма  . Нахождение   описано в статье линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами и нам осталось научиться определять  . Существует несколько методов нахождения частного решения ЛНДУ второго порядка с постоянными коэффициентами. Методы выбираются в зависимости от вида функции f(x), стоящей с правой части уравнения

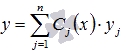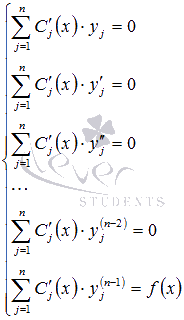Для любого другого вида функции f(x) общее решение ЛНДУ можно найти методом вариации произвольных постоянных. Вот на методе вариации произвольных постоянных остановимся подробнее. Если нам известны   - n линейно независимых частных решений соответствующего ЛОДУ, то, варьируя произвольные постоянные, общее решение ЛНДУ можно записать как  . Производные функций   находятся из системы уравнений   а сами функции   определяются при последующем интегрировании.

Вопрос №4 Линейное неоднородное дифференциальное уравнение

Рассмотрим линейное неоднородное дифференциальное уравнение y(n) + an-1y(n - 1) + ... + a1y' + a0y = f(x). Коэффициенты an-1, ... , a1, a0 — постоянные десйствительные числа, f(x) — непрерывная на [a, b] правая часть. Общее решение этого уравнения имеет вид y(x) = C1y1(x) + C2y2(x) + ... + Cnyn(x) + y*(x), где С1, С2, ..., Сn — произвольные постоянные, y1(x), y2(x), ..., yn(x) — фундаментальная система решений однородного уравнения, y*(x) — частное решение неоднородного уравнения.   Частное решение y*(x) можно найти методом подбора, если правая часть уравнения — квазимногочлен — функция вида f(x) = exp(αx)(Mm(x)cos(βx) + Nn(x)sin(βx)). Здесь Mm(x) — многочлен степени m, Nn(x) — многочлен степени n, α и β — действительные числа. Метод подбора вычисления частного решения линейного неоднородного уравнения с квазимногочленом в правой части состоит в том, что частное решение уравнения отыскивают в виде y*(x) = exp(αx)(Pk(x)cos(βx) + Qk(x)sin(βx))xr, где Pk(x) и Qk(x) — многочлены степени k = max(n, m) с неизвестными коэффициентами, Pk(x) = pkxk + pk-1xk-1 + ... + p1x + p0, Qk(x) = qkxk + qk-1xk-1 + ... + q1x + q0. Для того чтобы найти неизвестные коэффициенты многочленов Pk(x) и Qk(x) , подставляем y*(x) = exp(αx)(Pk(x)cos(βx) + Qk(x)sin(βx)) в уравнение и приравниваем в правой и левой части полученного равенства коэффициенты при exp(αx)cos(βx), exp(αx)sin(βx), xexp(αx)cos(βx), xexp(αx)sin(βx),  x2exp(αx)cos(βx), x2exp(αx)sin(βx), ...,   xkexp(αx)cos(βx), xkexp(αx)sin(βx). Полученная таким образом система 2k + 2 уравнений относительно 2k + 2 неизвестных имеет единственное решение.   Метод подбора применяется к ограниченному, но достаточно широкому классу правых частей, поскольку квазимногочленами являются функции вида: Mk(x),  Mk(x)exp(αx),  Mk(x)cos(βx),   Mk(x)sin(βx),  exp(αx)(Mm(x)cos(βx) + Nn(x)sin(βx)).   Частное решение y*(x) можно найти методом подбора, если правая часть уравнения — квазимногочлен — функция вида f(x) = exp(αx)(Mm(x)cos(βx) + Nn(x)sin(βx)). Здесь Mm(x) — многочлен степени m, Nn(x) — многочлен степени n, α и β — действительные числа. Метод подбора вычисления частного решения линейного неоднородного уравнения с квазимногочленом в правой части состоит в следующем. Внимательно смотрим на правую часть уравнения и записываем число α ± βi. Затем составим характеристическое уравнение однородного уравнения и найдем его корни. Возможны два случая: среди корней характеристического многочлена нет корня, равного числу α ± βi (нерезонансный случай) и среди корней характеристического многочлена есть rкорней, равных числу α ± βi ( резонансный случай). Рассмотрим нерезонансный случай (среди корней характеристического многочлена нет корня, равного числу α ± βi) . Тогда частное решение уравнения будем искать в виде y*(x) = exp(αx)(Pk(x)cos(βx) + Qk(x)sin(βx)), где Pk(x) и Qk(x) — многочлены степени k = max(n,m) с неизвестными коэффициентами, Pk(x) = pkxk + pk-1xk-1 + ... + p1x + p0, Qk(x) = qkxk + qk-1xk-1 + ... + q1x + q0. Для того чтобы найти неизвестные коэффициенты многочленов Pk(x) и Qk(x) , подставим y*(x) = exp(αx)(Pk(x)cos(βx) + Qk(x)sin(βx)) в уравнение и приравняем коэффициенты при exp(αx)cos(βx), exp(αx)sin(βx), xexp(αx)cos(βx), xexp(αx)sin(βx),  x2exp(αx)cos(βx), x2exp(αx)sin(βx), ...,   xkexp(αx)cos(βx), xkexp(αx)sin(βx). Доказано, что полученная таким образом система 2k + 2 уравнений относительно 2k + 2 неизвестных имеет единственное решение. Рассмотрим резонансный случай (среди корней характеристического многочлена есть r корней, равных числу α ± βi) . Тогда частное решение уравнения будем искать в виде y*(x) = exp(αx)(Pk(x)cos(βx) + Qk(x)sin(βx))xr, где Pk(x) и Qk(x) — многочлены степени k = max(n,m) с неизвестными коэффициентами. Для того чтобы найти неизвестные коэффициенты многочленов Pk(x) и Qk(x) , подставляем y*(x) = exp(αx)(Pk(x)cos(βx) + Qk(x)sin(βx))xr в уравнение и приравниваем коэффициенты при exp(αx)cos(βx), exp(αx)sin(βx), xexp(αx)cos(βx), xexp(αx)sin(βx),  x2exp(αx)cos(βx), x2exp(αx)sin(βx), ...,   xkexp(αx)cos(βx), xkexp(αx)sin(βx).

Вопрос №5 Основные типы уравнений математической физики Математическая физика — теория математических моделей физических явлений. Она относится к математическим наукам; критерий истины в ней — математическое доказательство. Однако, в отличие от чисто математических наук, в математической физике исследуются физические задачи на математическом уровне, а результаты представляются в виде теорем, графиков, таблиц и т. д. и получают физическую интерпретацию.  К основным уравнениям математической физики относятся следующие дифференциальные уравнения в частных производных второго порядка.  1. Волновое уравнение: .  Это уравнение является простейшим уравнением гиперболического типа. К его исследованию приводит изучение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводах и т.д.  2. Уравнение теплопроводности, или уравнение Фурье: .  Это уравнение является простейшим уравнением параболического типа. К его исследованию приводит рассмотрение процессов распространения тепла, фильтрации жидкости и газа в пористой среде, изучение некоторых вопросов теории вероятностей и т.д.  3. Уравнение Лапласа: .  Это уравнение относится к простейшим уравнениям эллиптического типа. К его исследованию приводит изучение задач об электрических и магнитных полях, о стационарном тепловом состоянии, задач гидродинамики и т.д.  В выписанных уравнениях искомая функция u зависит от двух переменных t, x или x, y. Рассматриваются также уравнения и для функций с большим числом переменных.