4.2 Определение геометрических параметров

конической передачи редуктора

Параметры зубчатой конической передачи с прямыми зубьями определены в соответствии с ГОСТ 19624-74. Зацепление передачи – эвольвентное, без смещения. Для зубчатых колес принята 7-я степень точности по нормам плавности.

Начальный средний диаметр шестерни (рис. 4.1), мм,

,

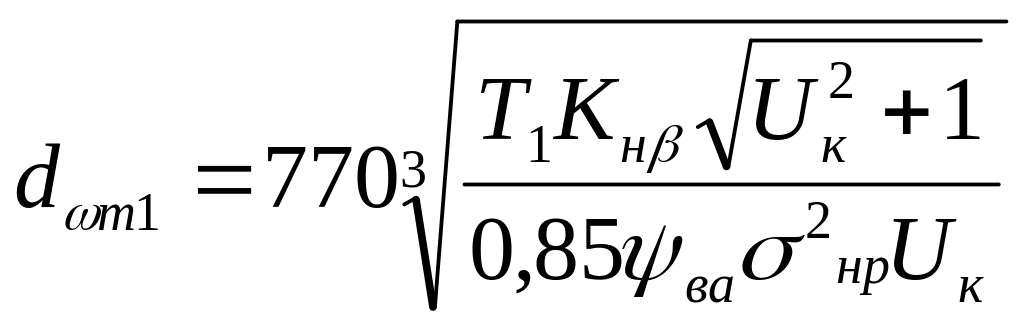где Т₁ – вращающий момент на выходном валу, Нм;

К_н – коэффициент неравномерности распределения нагрузки по длине контактных линий (рис. 4.2), принимается в зависимости от коэффициента зубчатого венца по делительному среднему диаметру шестерни

Принимаем: тогда

_нр – допускаемое контактное напряжение, МПа;

U_к – передаточное число конической передачи редуктора;

,

где – предел контактной выносливости поверхностей зубьев колеса, где HB₂ – твёрдость материала колеса соответственно, МПа;

– коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев, принимаем 0,9;

– коэффициент, учитывающий влияние окружной скорости, принимаем 1,0;

– коэффициент безопасности зубчатых колес.

– коэффициент долговечности,

Базовое число циклов напряжений, соответствующее пределу выносливости, млн. циклов:

Суммарное число циклов напряжения, млн. циклов:

где n₂ – частоты вращения шестерни и колеса соответственно, об/мин;

L_h – требуемый ресурс передачи, ч.

Так как , то коэффициент долговечности:

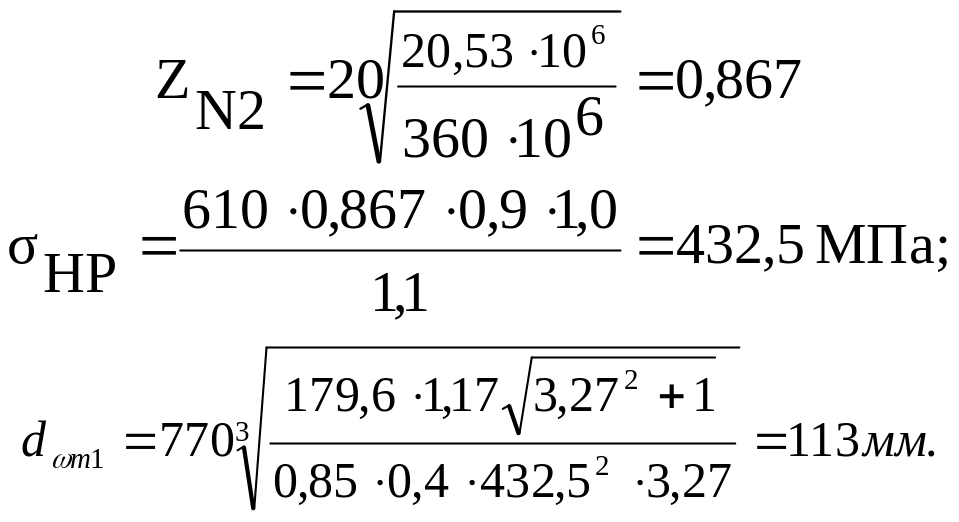
Число зубьев шестерни принимаем:

Число зубьев колеса:

Принимаем =72

Угол наклона делительного конуса шестерни

.

Угол наклона делительного конуса колеса

.

Средний модуль зубьев:

мм,

где делительный диаметр шестерни, .

Ширина зубчатого венца:

мм

Внешний окружной делительный модуль зубьев:

.

Округляем до ближайшего по ГОСТ 9563-60:

Средний модуль:

мм.

Значение m_m не округляют.

Начальный средний диаметр шестерни:

мм.

Окружная скорость передачи:

м/с,

где ₁ – угловая скорость входного вала, рад/с.

В соответствии с ГОСТ 13754-81 коэффициент высоты головки зубьев и коэффициент радиального зазора .

Высота головок зубьев:

мм

Высота ножек зубьев:

мм

Высота зубьев:

Делительные диаметры колес:

Внешние диаметры вершин d_ae и диаметры впадин d_fe:

для шестерни – ;

;

для колеса – ;

.

Внешнее конусное расстояние:

.

Среднее делительное конусное расстояние:

.

4.2.1 Проверочный расчёт зубьев колёс на контактную прочность

После определения геометрических размеров рабочие поверхности зубьев необходимо проверить на контактную прочность. Для этого определяем рабочие контактные напряжения _Н и сравниваем с допускаемыми _НР. Должно выполняться условие:

,

,

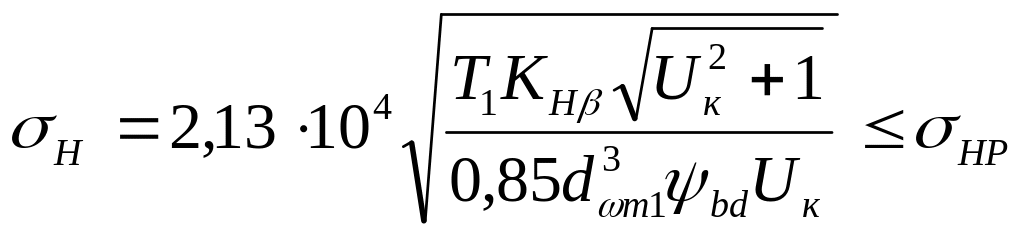где _Н – рабочее контактное напряжение, МПа;

 коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий после приработки,

,

где  коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий в начальный период работы передачи (из табл. 4.3 =1,17);

– коэффициент, учитывающий приработку зубьев (из табл. 4.4 =0,38).

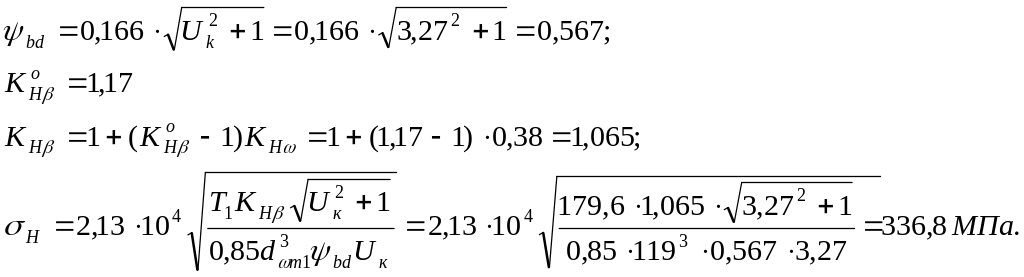
Условие прочности выполняется т.к: