3.2. Списки
Исходной операцией арифметики является унарная функция следования. Хотя при этом можно определять столь сложные рекурсивные функции, как функция Аккермана, использование унарной рекурсивной структуры является существенным ограничением. В данном разделе рассматривается бинарная структура - список .
Первый аргумент списка - это элемент, второй аргумент рекурсивно определяется как остаток списка. Списковых структур достаточно для большинства вычислений - об этом свидетельствует успех языка программирования Lisp, в котором списки являются основной составной структурой данных. С помощью списков можно представлять любые сложные структуры, хотя в иных конкретных задачах удобнее пользоваться специальными структурами данных.
При построении списков, как и при построении чисел, необходимо наличие константного символа, чтобы рекурсия не была бесконечной. Это “пустой список”, называемый nil, будем обозначать его знаком [ ]. Нам также требуется функтор арности 2. Исторически общепринятый функтор для списков обозначается “.”.Чтобы не перегружать обращение к символу “точка”, будем использовать специальную запись. Терм .(X,Y) будет обозначаться [X | У]. Компоненты терма имеют специальные названия: Х называется головой, а У хвостом списка,
Терм [Х | Y] соответствует в языке Lisp применению операции cons к паре X, Y Соответствующими названиями для головы и хвоста списка будут car и cdr.
Рис. 3.2 поясняет соотношение между различными способами записи списков. Первая колонка представляет запись списков с помощью функтора “.”, именно так термы логических программ задают списки. Вторая колонка представляет запись с помощью квадратных скобок, эквивалентную функтору “точка”. Третья колонка содержит выражения, являющиеся упрощением представлений второй колонки, при котором рекурсивная структура списка оказывается скрытой. В такой записи список представляется в виде последовательности элементов, ограниченной квадратными скобками и разделяемой запятыми. Пустой список, применяемый для завершения рекурсивного описания, явно не приводится. Отметим использование “cons-записи” в третьей колонке при описании списка, хвост которого - переменная.
Формальный Cons-запись Запись с помощью
объект элементов
.(a,[ ]) [a| [ ]] [a]
.(a, .(b,[ ])) [a| [b|[ ]]] [a,b]
.(a, .(b, .(c,[ ]))) [a|[b|[c|[ ]]]] [a,b,c]
.(a,X) [a|X] [a|X]
.(a, .(b,X)) [a|[b|X]] . [a|[b|X]]
Рис. 3.2. Эквивалентные записи списков.
list(Xs)
Xs-список.
list([ ]).
list([X|Xs]) list(Xs).
Программа 3.11. Определение списка.
С помощью функтора “.” строятся более общие термы, чем списки. Программа 3.11 является точным описанием списка. Декларативная интерпретация: “Списком является либо пустой список, либо значение функции cons на паре, хвост которой - список”. Эта программа подобна программе 3.1, задающей натуральные числа, и является определением простого типа для списков.
Рис. 3.3 содержит дерево вывода цели lisl([a, b ,c ]). В дереве вывода неявно содержатся основные примеры правила программы 3.11, например, list{[a,b, c]) list([b,c]). Мы приводим частный пример в явном виде, так как примеры списков в виде “cons-записи” могут сбить с толку. Список [а, b, с] является примером терма [Х|Хs] при подстановке [X = a,Xs = [b,с]}.
Поскольку списки являются более богатой структурой данных, чем числа, с ними связан больший набор полезных отношений. Фундаментальной операцией является, возможно, определение вхождения отдельного элемента в список. Предикатом. задающим это отношение, будет member (Element, List}. Программа 3.12 является рекурсивным описанием отношения memher/2.
Декларативное понимание программы 3.12 очевидно. Х является элементом списка, если в соответствии с первым предложением Х-голова списка или в соответствии со вторым предложением Х является элементом хвоста. Значение программы есть множество всех основных примеров цепи member (X,Xs), где X-элемент списка Хs, Мы опускаем типовое условие в первом предложении Первое предложение с условием запишется так:
member(X, [X | Xs]) list(Xs).
Рис. 3.3. Дерево вывода при проверке списка.
member (Element,List)
Element является элементом списка List.
member(X[X|Xs]).
member(X,[Y | Ys]) member(X, Ys).
Программа 3.12. Принадлежность списку.
Как будет показано в дальнейшем, эта программа имеет много интересных приложений. Основные применения состоят в проверке принадлежности элемента списку с помощью вопросов вида member(b[a,b,c])?, в нахождении элементов списка с помощью вопросов вида member(X,[a,b,с])? и списков, содержащих элемент, с помощью вопроса вида member (b,Х)?. Последний вопрос выглядит странным, однако имеется ряд программ, основанных на таком использовании отношения member.
Всюду, где это возможно, мы используем следующее соглашение о наименовании переменных в программах, использующих списки. Если символ Х используется для обозначения головы списка, то Xs для обозначения хвоста списка. В общем случае имена во множественном числе используются для обозначения списка элементов, а имена в единственном числе - для отдельных элементов. Числовые суффиксы обозначают различные варианты списков. Реляционные схемы по-прежнему содержат мнемонические имена.
Нашим следующим примером будет предикат sublist(Sub, List), служащий для определения, является ли список Sub подсписком списка List.Подсписок должен содержать последовательные элементы: так,[b, с] является подсписком списка [a,b,c,d], а [а,с] не является.
Для упрощения определения отношения sublist удобно выделить два специальных случая подсписков. Введение содержательных отношений в виде вспомогательных предикатов является правильным подходом к построению логических программ. Двумя рассматриваемыми случаями будут начальный подсписок (префикс списка) и конечный подсписок (суффикс списка). Программы представляют и самостоятельный интерес.
Предикат prefix(Prefix, List) истинен, если Prefix является начальным подсписком списка List, например, prefix([a,b],[a,b,c]) истинен. Предикатом, парным к prefix,будет предикат suffix (Suffix, List), утверждающий, что список Suffix является конечным подсписком списка List. Например, suffix([b,c],[a,b,c]) истинен. Оба предиката определены в программе 3.13. Для обеспечения корректности программ к годным фактам надо добавить типовое условие list(Xs).
Произвольный подсписок может быть определен в терминах префикса и суффикса,а именно как суффикс некоторого префикса или как префикс некоторого суффикса. Программа 3.14а задает логическое правило, согласно которому Хs
prefix(Prefix,List)
список Prefix есть префикс списка List
prefix([ ].Ys).
ргеfiх([Х|Xs],[X | Ys]) prefix(Xs.Ys).
suffix( Suffix .list)
список Suffix есть суффикс списка List.
suffix(Xs,Xs).
suffix(Xs,[Y | Ys]) suffix(Xs,Ys).
Программа 3.13. Префикс и суффикс списка.
sublist (Sub, List)
Sub есть подсписок списка List.
а: суффикс префикса
sublist(Xs,Ys) prefix(Ps,Ys),suffix(Xs,Ps).
b: префикс суффикса
sublist(Xs,Ys) prefix(Xs,Ss), suffix(Ss,Ys).
с: рекурсивное определение отношения sublist
sublist(Xs,Ys) prefix(Xs,Ys). sublist(Xs,[Y | Ys]) sublist(Xs,Ys).
d: суффикс префикса с использованием append
sublist(Xs,AsXsBs)
append(As,XsBs,AsXsBs),append (Xs,Bs,XsBs).
e: префикс суффикса с использованием append
sublist(Xs,AsXsBs)
append(AsXs,Bs,AsXsBs), append(As,Xs,AsXs).
Программа 3.14. Определение подсписка списка.
является подсписком Ys, если существует такой префикс Ps списка Ys, что Xs- суффикс списка Ps. Программа 3.14b задает двойственное определение подсписка как префикса некоторого суффикса.
Предикат prefix может быть также использован в качестве основы рекурсивного определения отношения sublist. Такое определение дается программой 3.14,с. Базовое правило гласит, что префикс списка является подсписком списка. В рекурсивном правиле записано, что подсписок хвоста списка является подсписком самого списка.
Предикат member можно считать частным случаем предиката sublist, задав правило
member (X,Xs) sublist ([X],Xs).
Основной операцией над списками является соединение двух списков для получения третьего. Эта операция задает отношение append (Xs,Ys,Zs) между двумя списками Xs, Ys и результатом их соединения, списком Zs. Программа 3.15. задающая append, имеет структуру, идентичную структуре программы 3.5 для отношения plus.
На рис. 3.4 приводится дерево вывода цели append([a,b],[c,d],[a,b,c,d]). Вид дерева наводит на мысль, что размер дерева линейно зависит от размера первого списка. В общем случае если список Xs содержит п элементов, то дерево вывода цели append(Xs,Ys,Zs) содержит п + 1 вершину.
append'( Xs.Ys, XsYs)
XsUs результат соединения списков Xs и Ys. append([ ], Ys, Ys).
append([X | Xs],[X | Zs]) append(Xs,Ys,Zs).
Программа 3.15. Соединение двух списков.
Рис. 3.4. Дерево вывода для соединения двух списков.
Как и в случае отношения plus, существуют разнообразные использования отношения append. Основное использование состоит в соединении двух списков в один с помощью вопроса вида append([a.b.c][d,e]Xs)?, ответом на который будет Xs =[a,b,c,d,e]. Поиск ответа на вопрос вида append(Xs[c,d],[a,b,c,d])? сводится к нахождению разности Xs = [а, b] между списками [c,d] и [a,b,c,d]. Однако в отличие от отношения plus первые два аргумента отношения append не симметричны, и поэтому существуют два различных варианта нахождения разности между двумя списками.
Процедурой, аналогичной разбиению натурального числа, является процедура расщепления списка. Например, при обработке вопроса append(As,Bs,[a,b,c,d])? ищутся такие списки As и Bs, что соединение списков As и Bs дает список [a,b,c,d]. Вопросы о расщеплении списка становятся более содержательными при частичном уточнении вида получаемых списков. Введенные выше предикаты member, sublist, prefix и suffix могут быть определены в терминах предиката append, если последний использовать для расщепления списков.
Наиболее просто определяются предикаты prefix и suffix, в определении непосредственно указывается, какая из двух частей расщепления нас интересует:
prefix (Xs,Ys) append(Xs,As,Ys).
suffix(Xs,Ys) append(As,Xs,Ys).
Отношение sublist определяется с использованием двух целей вида append. Существуют два различных варианта определения, они приведены в программах 3.14d и 3.14е. Эти две программы получены соответственно из программ 3.14а и 3.14Ь заменой целей вида prefix и suffix на их выражения в терминах предиката append.
Отношение member может быть определено через отношение append следующим образом:
member(X,Ys) append(As,[X Xs],Ys).
В определении сказано, что Х является элементом списка Ys, если Ys может быть Расщеплен на два списка, причем Х- голова второго списка,
Аналогичное правило может быть приведено для отношения adjacent (X,Y,Zs), истинного, если Х и Y являются соседними элементами списка Zs:
adjacent(X,Y,Zs) append (As, [X, Y | Ys],Zs).
Другое отношение, легко задаваемое с помощью отношения append, состоит в определении последнего элемента списка. В правиле указывается, что второй аргумент предиката append должен иметь вид списка из одного элемента:
last(X,Xs) append(As,[X],Xs).
Многократное применение предиката append может быть использовано для определения отношения reverse (List, Tsil). Подразумеваемое значение предиката reverse состоит в том, что список Tsil содержит элементы списка List, расположенные в обратном порядке по сравнению с порядком в списке List. Примером цели, входящей в подразумеваемое значение программы, является reverse([a,b,c],[c,b,a])Простейший вариант, приведенный в программе 3.16а, является логическим эквивалентом рекурсивного определения на естественном языке: рекурсивно обратить хвост списка и добавить затем первый элемент в конец обращенного хвоста.
reverse (List,Tsil)
список Tsil есть обращение списка List.
а: “наивное” обращение списка
reverse([ ],[ ])
reverse([X | Xs],Zs) reverse(Xs,Ys), append(Ys,[X],Zs).
b: обращение с накоплением reverse(Xs,Ys) reverse(Xs,[ ],Ys).
reverse([X | Xs],Acc,Ys) +- reverse(Xs,[X | Acc],Ys). reverse([ ],Ys,Ys).
Программа 3.16. Обращение списка.
Имеется иной способ определения предиката reverse (Xs,Ys,Zs), прямо не использующий обращений к предикату append. Определим вспомогательный предикат reverse (Xs,Ys,Zs), истинный, если Zs- результат соединения списка Ys с элементами обращенного списка Xs. Это определение приведено в программе 3.16b. Связь предикатов reverse/3 и reverse/2 задана в первом правиле программы 3.16b.
Программа 3.16b эффективнее программы 3.16а. Рассмотрим рис. 3.5, на котором приведено дерево вывода цели reverse([a,b,c,d],[d,c,b,d]) для обеих программ. В общем случае размер дерева вывода для программы 3.16а квадратично зависит от размера обращаемого списка, в то время как для программы 3.16b эта зависимость линейна.
Преимущество программы 3.16b обусловлено лучшей структурой данных, представляющих последовательность элементов; мы обсудим это подробнее в гл. 7 и 15.
Последняя программа этого раздела, программа 3.17, выражает отношение между числами и списками, основанное на рекурсивной структуре этих объектов. Предикат length (Xs,N) истинен, если длина списка Xs равна N, то есть список Xs содержит N элементов, где N натуральное число. Например, length([a,b],s(s)0))) означает, что список [a,b] содержит два элемента, эта цель принадлежит значению программы.
length(Xs.N)
список Xs содержит N элементов.
length([ ],0).
length([X | Xs],s(N)) lenglh(Xs,N).
Программа 3-17. Определение длины списка.
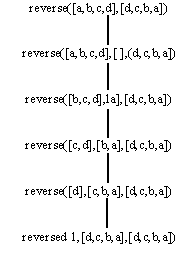
Рис. 3.5. Дерево вывода при обращении списка.
Давайте рассмотрим различные возможности использования программы 3.17. Вопрос lenthg([a,b],Х)? сводится к вычислению длины списка [a,b], равной 2. В этом случае length рассматривается как функция от списка, имеющая функциональное определение
length([ ]) = 0.
length([X,Xs]) = s(length(Xs)).
В вопросе length([a,b],s(s(0)))проверяется, имеет ли список [а,b] длину 2. Вопрос length(Xs,s,(s(0)))? порождает списки длины 2 с различными элементами.
Упражнения к разд 3.2
• Следующие три правила задают вариант программы 3.14 для отношения sublist:
subsequence([X | Хs],ГХ Ys]) subsequence(Xs,Ys), subsequence(Xs,[Y | Ys]) subsequence (Xs,Ys).
subsequence([ ],Ys).
Объясните, почему значение этой программы отличается от значения программы 3.14.
• Напишите рекурсивные программы для предикатов adjacent и last с теми же значениями что и у предикатов, определенных ранее через append.
Напишите программу для отношения double(List,List List), в котором каждый элемент списка List удваивается в списке List List, например, double ([1,2,3],[1,1,2,2,3,3]) выполнено.
4. Определите размер дерева вывода как функцию от размера входного списка для программ 3.16а и 3.16b, определяющих отношение reverse.
5. Определите отношение sum (ListOfInteger,Sum), которое выполнено, если число Sum является суммой элементов списка List Of Integer:
а) используя предикат plus/3;
б) без использования каких-либо вспомогательных предикатов. (Замечание: достаточно трех аксиом.)