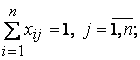13.4. Примеры задач целочисленного программирования
Задача
о коммивояжере.
Имеется n
городов. Выезжая из одного, коммивояжер
должен объехать все и вернуться в
исходный. В каждый город можно заезжать
только один раз, поэтому маршрут
коммивояжера образует замкнутый цикл
без петель. Задана матрица
расстояний
между городами (считаем, что
);
разумеется
.
Матрица расстояний не предполагается
симметричной. Требуется найти кратчайший
замкнутый маршрут.
Построим математическую модель задачи, обозначая:
где
.
Требуется минимизировать
(13.34)
при условиях
(13.35)
(13.36)
(13.37)
Здесь
и
–
произвольные вещественные значения.
Покажем, что модель (13.34) – (13.37) описывает задачу о коммивояжере. Действительно, условие (13.35) означает, что торговец из каждого города выезжает только один раз; (13.36) – въезжает в каждый город только один раз; (13.37) – обеспечивает замкнутость маршрута, содержащего n городов, и отсутствие петель.
Задача о коммивояжере наиболее эффективно решается методом ветвей и границ. Имеет большое прикладное значение.
Задача
о назначениях.
Пусть требуется выполнить n
различных работ и имеется n
механизмов (машин) для их выполнения,
причем каждый механизм может использоваться
при любом типе работ. Производительность
каж-дого механизма на различных работах
может быть различной. Обозначим через
производительность
i-го
механизма на j-й
работе. Пусть каждый механизм может
выполнять только одну какую-либо работу.
Задача заключается в таком распределении
механизмов по работам, при котором
суммарная производительность максимальна.
Построим
математическую модель этой задачи.
Сопоставим каждому из возможных вариантов
распределения машин по работам набор
значений неизвестных
,
относительно которых условимся, что
,
если в данном варианте i-й
механизм назначается на j-ю
работу, и
,
если i-й
механизм назначается не на j-ю
работу. Для любого варианта среди чисел
должно
быть точно n
единиц, причем должны выполняться
следующие условия:
(каждый механизм назначается на одну работу) и
(на каждую работу назначается один механизм). Суммарная производительность при данном варианте назначения машин на работы выразится суммой
.
Таким образом, математическая модель задачи о назначениях будет такой:
при условиях
