3.1 Системы счисления и кодирования

 

3.1.1 Непозиционные системы счисления

3.1.2 Позиционные системы счисления

3.1.3 Двоичная система счисления

3.1.4 Другие системы счисления, используемые в компьютерных технологиях

 

Изучение систем счисления, арифметических и логических операций очень важно для понимания того, как происходит обработка данных в вычислительных машинах.

Любой компьютер может быть представлен как арифметическая машина, реализующая алгоритмы путем выполнения арифметических действий. Эти  арифметические действия производятся над числами, представленными в принятой системе счисления, в заданных форматах и с использованием специальных машинных кодов.

Совокупность приемов наименования и записи чисел называется системой счисления. В любой системе счисления числа записываются как последовательность символов. Счисление представляет собой частный случай кодирования, где слово, записанное с использованием определенного алфавита и по определенным правилам, называется  кодом. Применительно к счислению это код числа.

В любой системе счисления выбирается алфавит, представляющий собой совокупность некоторых символов (цифр или знаков), с помощью которого можно представить любое число. Символы алфавита должны быть разными и значение каждого из них должно быть известно.

С давних времен применялись различные системы счисления. Например, на Древнем Востоке и в Англии довольно широко была распространена двенадцатеричная система, а в Древнем Вавилоне существовала весьма сложная шестидесятеричная система. В современном мире наиболее распространенной является десятичная система счисления (арабская), происхождение которой связано с пальцевым счетом. Она возникла в Индии и в XIII веке была перенесена в Европу арабами.

Все системы счисления можно разделить на позиционные и непозиционные.

 

3.1.1 Непозиционные системы счисления

Вверх

 

В непозиционных системах счисления значения цифры или символа не зависит от положения в ряду цифр или символов, изображающих число. Примером этой системы счисления может служить  римская система счисления.

В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются, например  VI = 5+1 = 6. Если же слева записана меньшая цифра, а справа - большая, то их значения вычитаются, например  IV = 5-1 = 4.

В римской системе счисления используются латинские буквы: I-1, V-5, X-10, L-50, C-100, D-500, M-1000.  I - в записи чисел есть всегда единица и для девяти IX и для двенадцати - XII. В непозиционных системах счисления не представлены дробные и отрицательные числа.

Непозиционные системы счисления возникли намного раньше позиционных. Основной недостаток непозиционных систем – большое число разных знаков и сложность выполнения арифметических операций.

 

3.1.2 Позиционные системы счисления

Вверх

 

Если значение цифры или символа зависит от позиции в ряду цифр или символов изображающих число, то такая система счисления называется позиционной. Примером позиционной системы счисления является используемая нами десятичная система счисления. В ней любое число записывается с помощью десяти цифр: 0,1,2,3,4,5,6,7,8,9. Например, в записи 777 цифра 7 встречается три раза, но в каждой позиции она имеет разный смысл: крайняя левая цифра 7 означает сотни, следующая - десятки, и следующая цифра 7 - единицы. Позиционные системы счисления более удобны для вычислительных операций, поэтому они получили наибольшее распространение.

Количество используемых цифр называется основанием позиционной системы счисления. Место для цифры в числе называется разрядом, а количество цифр в числе - разрядностью числа.

Например, 1999 - является 4-разрядным числом. Разряды нумеруются справа налево, и каждому разряду соответствует степень основания: .   Тогда, число 1999 представляется в системе с десятичным основанием, как

.

Крайняя слева цифра называется цифрой старшего разряда, а крайняя справа - цифрой младшего разряда.

Позиционная система счисления характеризуется основанием. Основание  позиционной  системы  счисления – количество знаков или символов, используемых в разрядах для отображения числа в данной системе счисления. В современных компьютерах используют позиционные системы счисления с основаниями: 2, 8, 10, 16, 32.

Любое число в позиционной системе счисления со степенными весами разрядов можно представить в виде ряда:

 

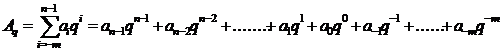 (3.1)

 

где,  

 - запись числа в системе счисления с основанием q;    

q - основание системы счисления;

- целое положительное число, меньше q;

n – число разрядов в целой части числа;

m – число разрядов в дробной части числа.

Таким образом, любое число можно разложить в сумму по степеням основания системы счисления в виде (3.1).

На практике используют сокращенную запись чисел, т.е.

                    (3.2)

Так как за основание можно принять любое целое число, возможно множество позиционных систем, например, двоичная, восьмеричная, десятеричная, шестнадцатеричная. При этом в двоичной системе алфавит состоит из двух цифр: 0 и 1; в десятеричной – из десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; в шестнадцатеричной – из цифр 0…9 и символов А, B, C, D, E, F для обозначения цифр 10, 11, 12, 13, 14, 15 соответственно.

Чем больше основание системы  счисления, тем меньшее число разрядов требуется для представления данного числа, следовательно, и меньшее время для его передачи. Однако, с ростом основания существенно повышаются требования к аппаратуре формирования и распознавания элементарных сигналов, соответствующих различным символам. Логические элементы вычислительных устройств в этом случае должны иметь большее число устойчивых состояний.

Десятичная система счисления, привычная для нас в повседневной жизни, также не является наилучшей для использования в ЭВМ. Так как функциональные элементы с десятью устойчивыми состояниями имеют низкую скорость переключения и, таким образом, не могут удовлетворять требованиям, предъявляемым к ЭВМ по быстродействию.

В большинстве случаев в ЭВМ используют двоичные или двоично-кодированные системы счисления. Широкое распространение этих систем обусловлено тем, что элементы ЭВМ способны находиться лишь в одном из двух устойчивых состояний. Задача различения сигналов сводится в этом случае к задаче обнаружения (есть импульс или его нет), что значительно проще. Если одно из таких устойчивых состояний принято за 0, а другое – за 1, то достаточно просто изображаются разряды двоичного числа. Любому дискретному сообщению или знаку сообщения можно присвоить какой-либо порядковый номер Так будет получен один из кодов, основанный на данной системе счисления.

Таким образом, системы счисления используются для построения на их основе различных кодов в системах передачи, хранения и преобразования информации.