
4. Дифракционная решетка.
Дифракционные
световые пучки, исходящие от каждой
из![]() щелей
перекрываются, и интерферируют между
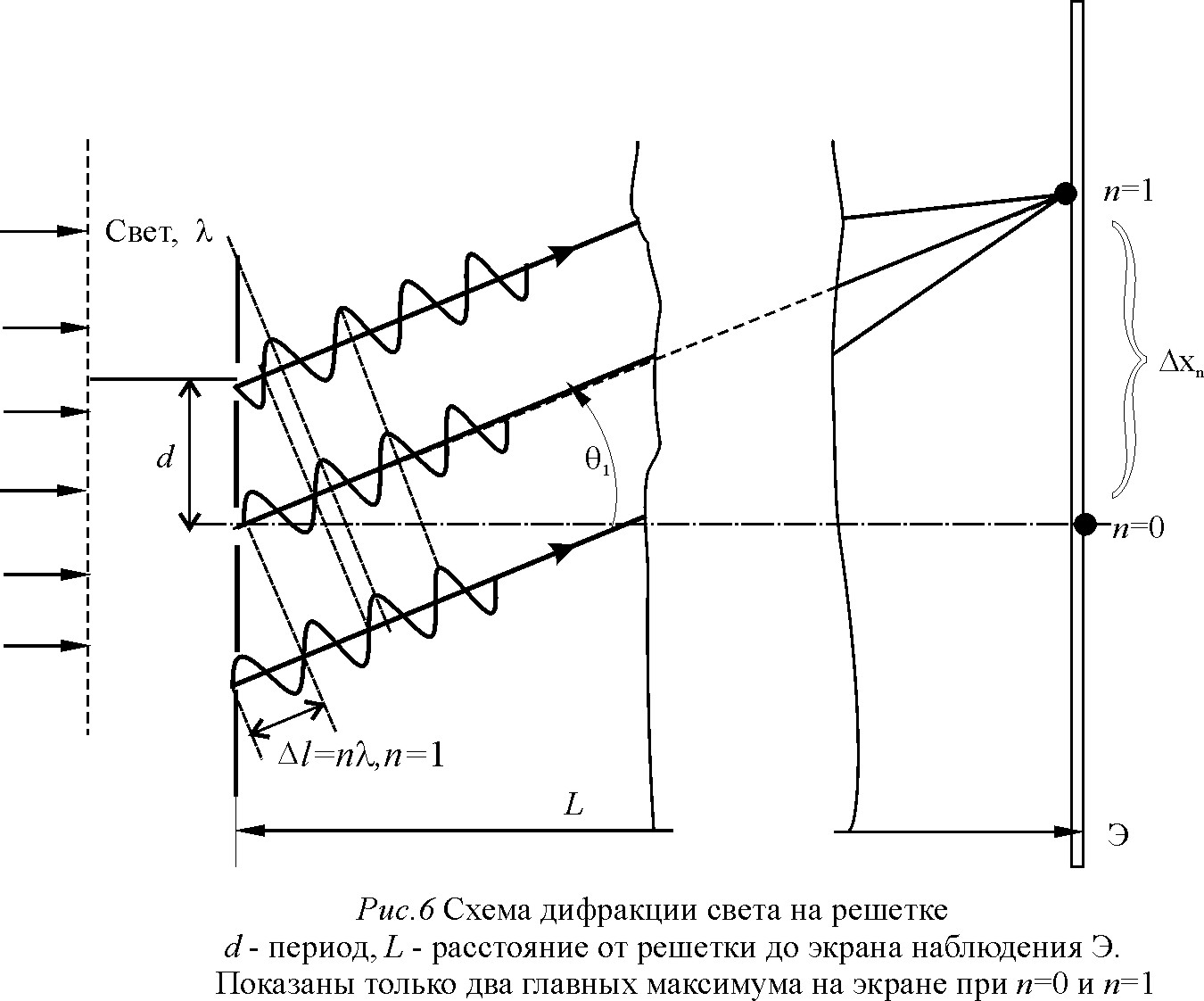
собой. (Рис.6) Происходит дополнительное
перераспределение интенсивности по
углам дифракции. В результате дифракции
на периодической структуре щелей свет
за решёткой может распространяться в
основном только в нескольких, так
называемых главных направлениях, которые
характеризуются углами
щелей
перекрываются, и интерферируют между
собой. (Рис.6) Происходит дополнительное
перераспределение интенсивности по
углам дифракции. В результате дифракции
на периодической структуре щелей свет
за решёткой может распространяться в
основном только в нескольких, так
называемых главных направлениях, которые
характеризуются углами
![]() ,
определяемых условием
,
определяемых условием
![]()
 ,
,
![]()
В
этом случае волны усиливают друг друга
при интерференции, и суммарная
интенсивность
![]() где
где
![]() - интенсивность от одной щели.
- интенсивность от одной щели.
![]()
 ,
то есть, интенсивность света,
распространяющегося под углом
и приходящего в точку
,
то есть, интенсивность света,
распространяющегося под углом
и приходящего в точку
![]() на экране наблюдения, в результате
интерференции возрастает в
на экране наблюдения, в результате
интерференции возрастает в
![]() раз по сравнению с интенсивностью
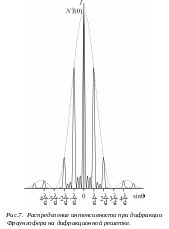
в этой же точке от одной щели. (Рис.7)
раз по сравнению с интенсивностью
в этой же точке от одной щели. (Рис.7)
Методом векторных диаграмм, можно получить:
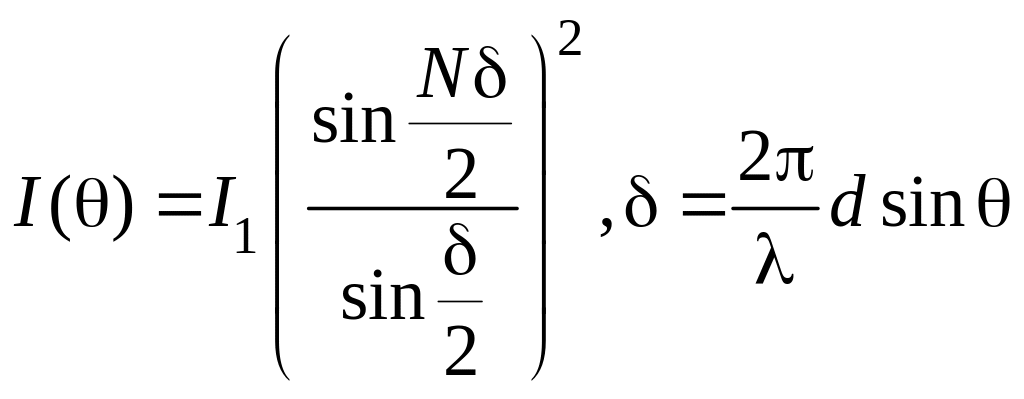 (*)-
распределение интенсивности при
дифракции света на амплитудной решетке,
где
(*)-
распределение интенсивности при
дифракции света на амплитудной решетке,
где![]() –
распределение интенсивности при
дифракции света на одиночной щели ;
–
распределение интенсивности при
дифракции света на одиночной щели ;
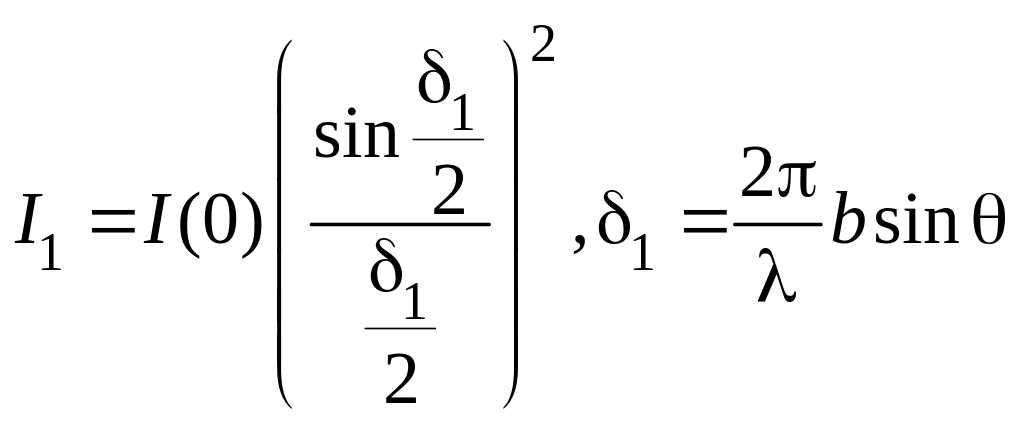
Н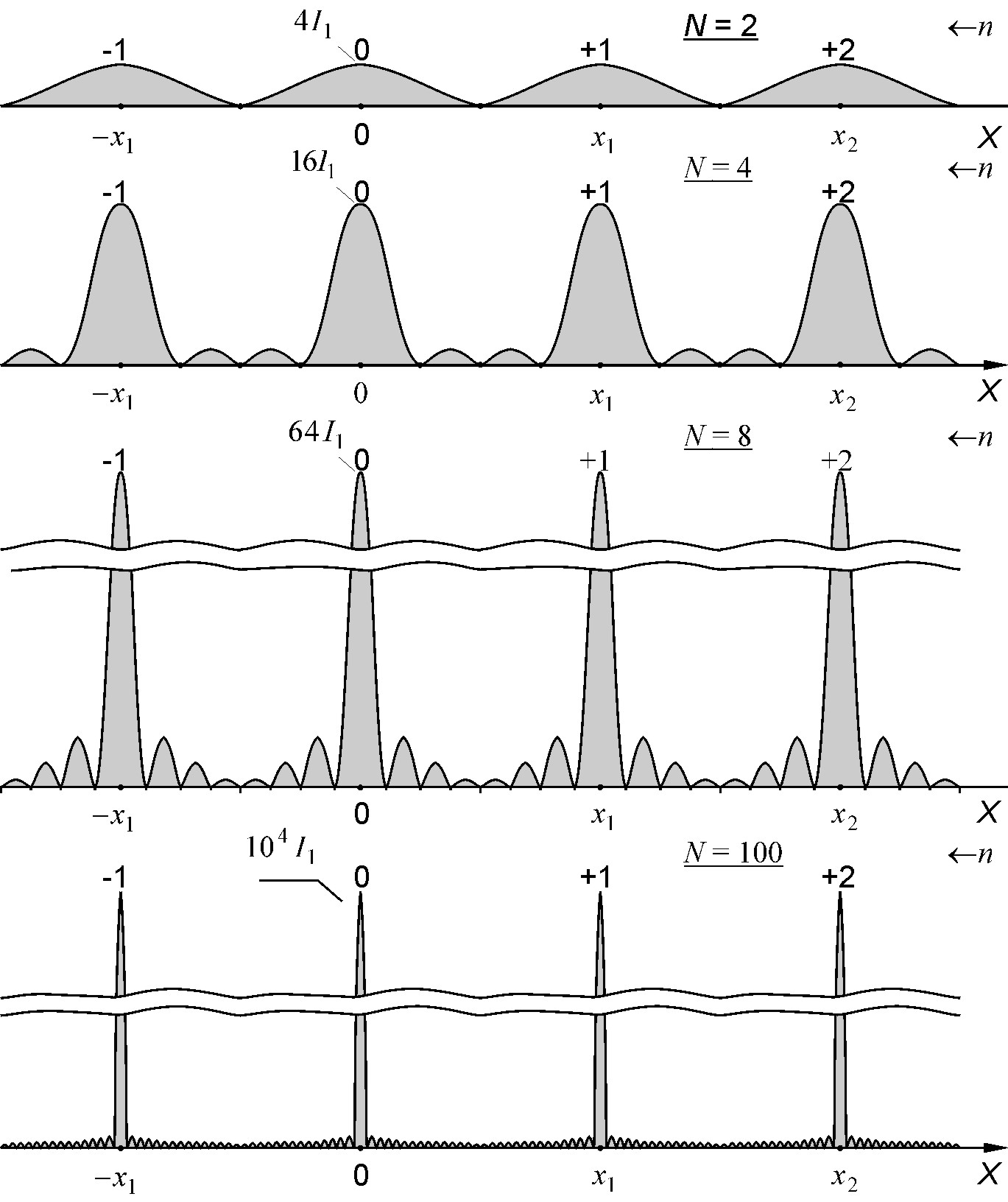 а
рис.8 показаны кривые распределения
интенсивности
а
рис.8 показаны кривые распределения
интенсивности
![]() при N = 2, N = 4, N =8, N = 100 для случая изотропных
источников, у которых интенсивность
испускаемых волн не зависит от направления
(от угла )
и
при N = 2, N = 4, N =8, N = 100 для случая изотропных
источников, у которых интенсивность
испускаемых волн не зависит от направления
(от угла )
и
![]() .
Графики построены в соответствии с
формулой (*) при малых углах, когда
.
Графики построены в соответствии с
формулой (*) при малых углах, когда
![]() .
.
Рис.8. Распределение интенсивности в интерференционных картинах, полученных от N источников
Обратите внимание, что количество дополнительных максимумов и минимумов в дифракционной картине связано с числом щелей N решетки
Число доп. максимумов =N-2
Число доп. минимумов =N-1
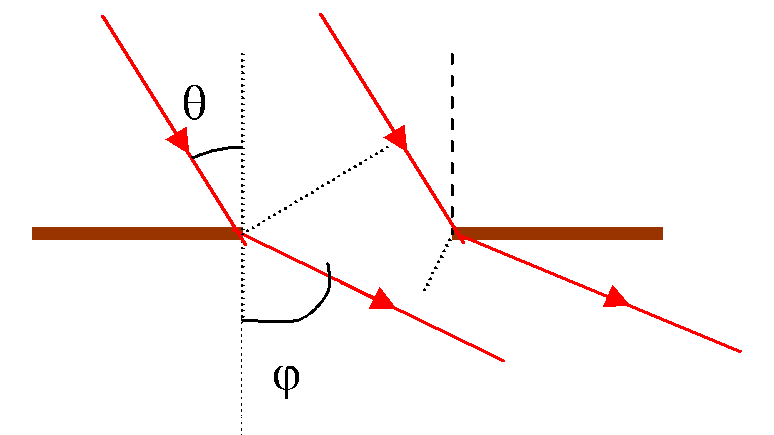 Если
рассмотреть наклонное
падение
волны на дифракционную решетку, то
разность хода между крайними точками
равна
Если
рассмотреть наклонное
падение
волны на дифракционную решетку, то
разность хода между крайними точками
равна![]() отсюда условие минимумов
отсюда условие минимумов![]() ,
(рис.9) Рис.9
,
(рис.9) Рис.9
5. Дифракционная решетка как спектральный прибор.
Положение
узких главных максимумов зависит от
длины волны
![]() .
Это позволяет использовать решетку в
качестве спектрального прибора. Решетка
способна разлагать свет в спектр. Для
этого могут быть использованы дифракционные
максимумы различных порядков (кроме
m = 0).
Практически, однако, используются
главные максимумы, расположенные в
пределах основного лепестка диаграммы
излучения одиночной щели, имеющего
полуширину
.
Это позволяет использовать решетку в
качестве спектрального прибора. Решетка
способна разлагать свет в спектр. Для
этого могут быть использованы дифракционные
максимумы различных порядков (кроме
m = 0).
Практически, однако, используются
главные максимумы, расположенные в
пределах основного лепестка диаграммы
излучения одиночной щели, имеющего
полуширину![]() .
Отсюда можно получить оценку:
.
Отсюда можно получить оценку:
![]() .
.
Угловая дисперсия
Угловой дисперсией спектральных приборов называется величина
![]()
В случае решетки, угловая дисперсия равна
![]()
Приближенное
выражение
![]() справедливо
в случае малых дифракционных углов.
справедливо
в случае малых дифракционных углов.
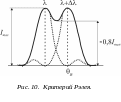
Разрешающая способность
Разрешающей способностью спектрального прибора принято называть отношение
![]() ,
,
где
![]() –
минимальный интервал между двумя
близкими спектральными линиями, при
котором они могут быть разрешены, то
есть, отделены одна от другой. В качестве
критерия разрешения используется обычно
критерий
разрешения Рэлея.
Спектральные линии с близкими значениями
и
–
минимальный интервал между двумя
близкими спектральными линиями, при
котором они могут быть разрешены, то
есть, отделены одна от другой. В качестве
критерия разрешения используется обычно
критерий
разрешения Рэлея.
Спектральные линии с близкими значениями
и
![]() считаются
разрешенными, если главный максимум
дифракционной картины для одной
спектральной линии совпадает по своему
положению с первым дифракционным
минимумом для другой спектральной линии
(см. рис.10).
считаются
разрешенными, если главный максимум
дифракционной картины для одной
спектральной линии совпадает по своему
положению с первым дифракционным
минимумом для другой спектральной линии
(см. рис.10).
![]()
Лекционные демонстрации
Натурный эксперимент
1. Демонстрация дифракции на CD диске.
Видеодемонстрации
Показ компьютерных демонстраций.
Модель1. Дифракционная решетка.
В
компьютерной модели ( рис.11) можно
изменять п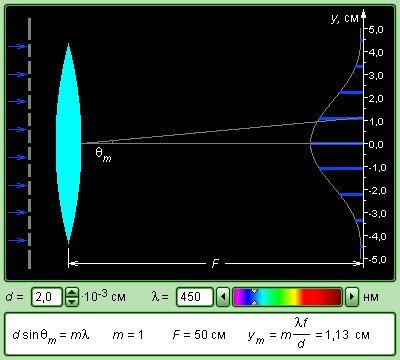 ериод
решетки d
и длину световой волны λ. Можно выбирать
номер m
с помощью наведения мышью на выбранный
главный максимум. На дисплее высвечивается
координата ym
выбранного максимума на экране,
расположенном в фокальной плоскости
линзы. Необходимо
обратить внимание студентов
на то, что масштабы по горизонтали и
вертикали отличаются приблизительно
в 5 раз. Поэтому изображаемые на экране
углы θm
сильно преувеличены. Рис.11
ериод
решетки d
и длину световой волны λ. Можно выбирать
номер m
с помощью наведения мышью на выбранный
главный максимум. На дисплее высвечивается
координата ym
выбранного максимума на экране,
расположенном в фокальной плоскости
линзы. Необходимо
обратить внимание студентов
на то, что масштабы по горизонтали и
вертикали отличаются приблизительно
в 5 раз. Поэтому изображаемые на экране
углы θm
сильно преувеличены. Рис.11
Модель 2. Разрешающая способность (рис.12).
Пусть, например,
N
= 8, b
= 10 мкм и d
= 100 мкм.
Выберем
=
500 нм,
![]() =
10 нм.
=
10 нм.
В каком порядке решетка разрешает такие спектральные компоненты?
Т.к.![]() ,
получим R
= 50. Легко
убедиться,
используя клавишу «Лупа», что выбранная
решетка разрешает такие спектральные
компоненты только в 6-ом порядке. Увеличив
число щелей до N
= 100, можно наблюдать разрешение этих
компонент уже в первом порядке.
,
получим R
= 50. Легко
убедиться,
используя клавишу «Лупа», что выбранная
решетка разрешает такие спектральные
компоненты только в 6-ом порядке. Увеличив
число щелей до N
= 100, можно наблюдать разрешение этих
компонент уже в первом порядке.
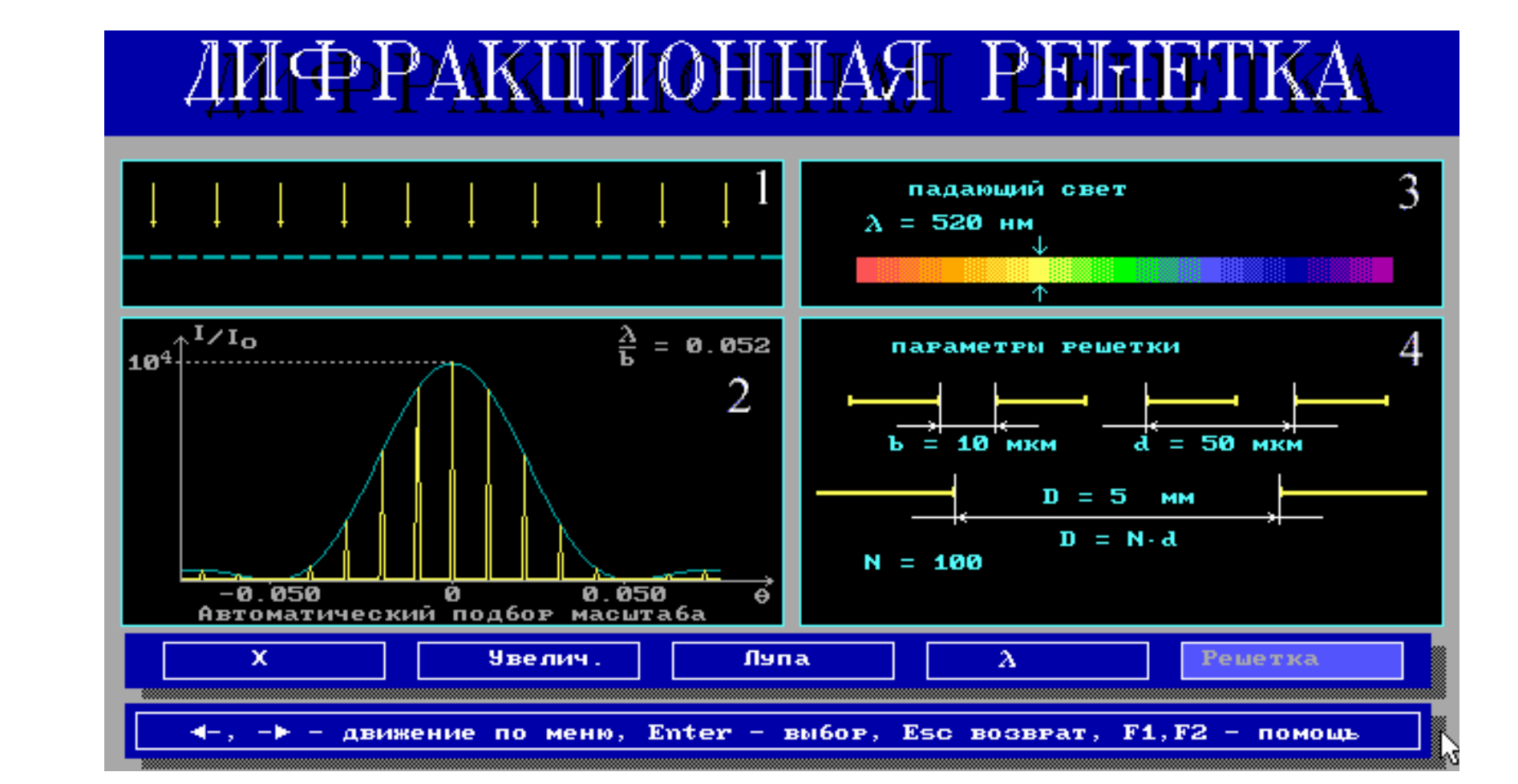 Рис.
12.
Рис.
12.
Дифракционная решетка как спектральный прибор.
1 - дифракционная решетка; 2 - график распределения интенсивности в дифракционной картине; 3 - параметры света; 4 -параметры решетки.

а)- выбор масштаба графика 2; b) -возможность увеличения графика 2; с) -возможность увеличения участка графика 2; d) -выбор параметров света; e) -выбор параметров решетки.
Учебно-методические материалы
Основная литература
1. Савельев И. В. Курс общей физики, кн. 3. – М.: ООО «Издательство Астрель», ООО «Издательство АСТ», 2004, §§5.5-5.6 .
2. Иродов И. Е. Волновые процессы. Основные законы: Учебное пособие для вузов. – М.: Бином. Лаборатория базовых знаний, 2007, §§ 5.4-5.8.
Дополнительная литература
3. Сивухин Д.В. Общий курс физики. т. 4. М.: ФИЗМАТЛИТ, 2009, §§44-47.
4. Ландсберг Г.С. Оптика. -М.,: ФИЗМАТЛИТ, 2003, §§39, 46.
5. Лосев В.В. Оптические явления. Теория и эксперимент. Учебное пособие, М., 2002, §§3.1 - 3.4.
Информационно-справочные ресурсы
6. [Электронный ресурс].-М.: Коллекция электронных ресурсов МИЭТ, 2007.- Режим доступа: http://orioks.miet.ru/oroks-miet/srs.shtml
7. Программа обучения. «Открытая Физика 2.6. Часть 2»:
http://www.physics.ru/
http://www.physics.ru/courses/op25part2/design/index.htm
8. Scientific Center «PHYSICON»: of the course «Wave Optics on the Computer»
http://college.ru/WaveOptics/content/chapter1/section1/paragraph1/theory.html
9. Диск или программа «Физика в анимациях»
http://physics.nad.ru/
http://physics.nad.ru/Physics/Cyrillic/optics.htm
