4 . Полосы равного наклона и равной толщины. Отражение от тонких пленок и плоскопараллельных пластинок. Кольца Ньютона. Интерферометры.

Рассмотрим отражение монохроматического света с длиной волны от пластинки толщиной . Схема отражения показана на рис.7 .

Световая волна, падающая под углом , частично отражается от верхней поверхности пластинки (луч 1). После преломления и отражения от нижней Рис.7

поверхности часть света возвращается обратно (луч 2). Результат сложения двух отраженных волн можно наблюдать на экране Э, установленном в фокальной плоскости линзы Л. Роль линзы и экрана может выполнять хрусталик и сетчатка нашего глаза.

Оптическая разность хода волн зависит от угла и от толщины . Начиная от точки деления падающего луча (точка А) на отраженный и преломленный можно проследить ход лучей 1 и 2 и найти разность проходимых оптических путей (разность хода ) до секущей плоскости . От плоскости до экрана оптические пути одинаковы. Поэтому , где - показатель преломления пластинки, и учтено, что волна 1 при отражении от пленки испытывает "потерю полуволны ". Из геометрии хода лучей, используя закон преломления , можно получить следующее выражение для разности оптических путей волн 1 и 2, приходящих на экран:

, где .

Каждой координате темной полосы соответствует определенный угол падения света на пластинку . Поэтому интерференционные полосы в этом случае называют полосами равного наклона.

Д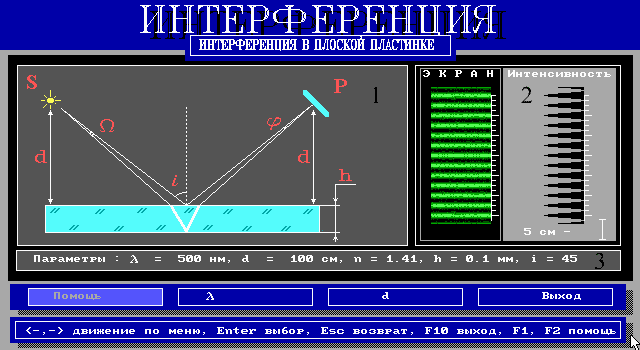 ЕМОНСТРАЦИЯ КОМПЬЮТЕРНОЙ МОДЕЛИ (см. описание выше). Изменяя параметры схемы, наблюдаем за распределением интенсивности на экране)

Рис.8

Кольца Ньютона

В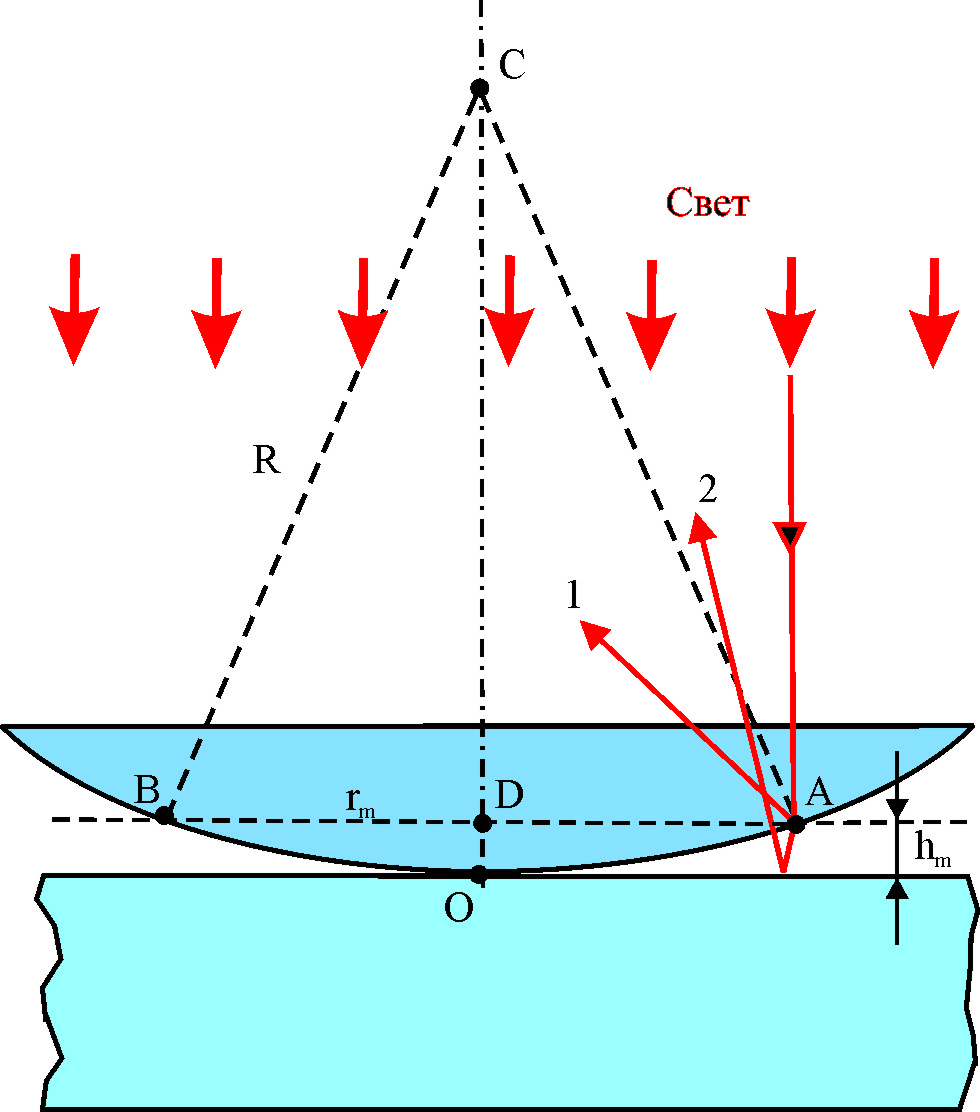 отраженном свете интерференционная картина является результатом сложения когерентных волн 1 и 2, отраженных от сферической поверхности линзы и от поверхности стеклянной пластинки (рис.9). Интенсивности волн примерно одинаковы, поэтому наблюдается довольно четкая (контрастная) система светлых и темных колец.

Выведем формулу для диаметров темных колец Ньютона в отраженном свете. Темные кольца радиуса r_m образуются в тех местах, где разность хода l_m волн 2 и 1 равна нечетному числу полуволн:

-для радиусов темных интерференционных колец Ньютона

- для радиусов светлых интерференционных колец Ньютона. Рис.9

Каждой координате x_m, т.е. каждой темной интерференционной полосе (темному кольцу), соответствует определенная толщина воздушной прослойки

(клина) под ней.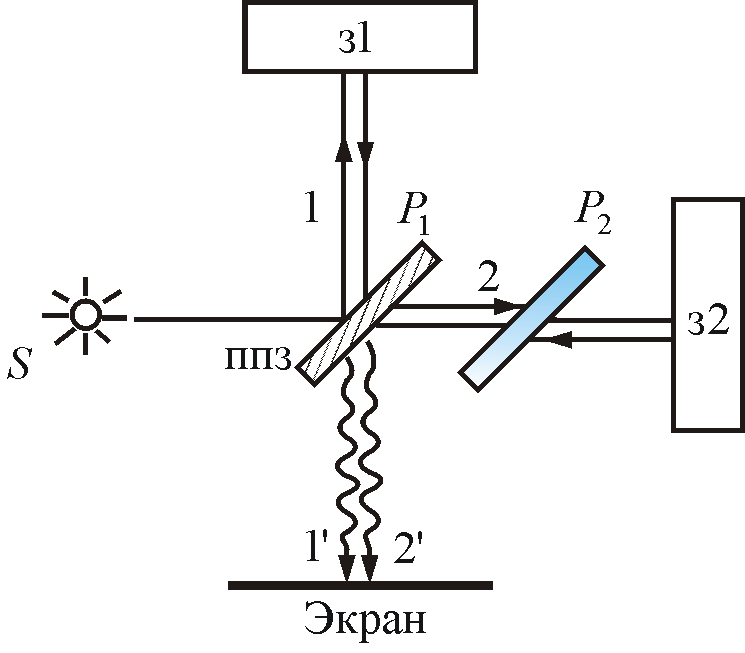 Поэтому интерференционные полосы в этом случае называют полосами равной (постоянной )толщины.

Для наблюдения как полос равного наклона, так и полос равной толщины можно использовать интерферометр Майкельсона (рис. 10). Рассмотрим схему интерферометра Майкельсона: з₁ и з₂ зеркала. Полупрозрачное зеркало P₁ посеребрено и делит луч на две части – луч 1 и 2. Луч 1, отражаясь от з1 Рис.10

и проходя P₁ , дает 1' , а луч 2, отражаясь от з2 и далее от P₁ , дает 2' . Пластинки P₁ и P₂ одинаковы по размерам. P₂ ставится для компенсации разности хода второго луча. Лучи 1' и 2' когерентны и интерферируют.

Л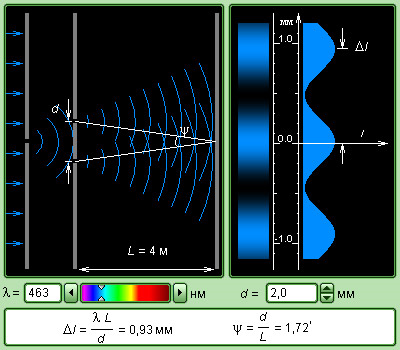 екционные демонстрации

Видеодемонстрации

1. Показ фрагмента видеофильма (Длительность всего фильма: 19 мин) Интерференция. Сложение волн. Когерентность Автор сценария: А.Смирнов Консультанты: д.физ-мат.н., профессор Т.Д. Шермергор, к.физ-мат.н. Ю.Иванов, к.физ.-мат.н. С. Пеньков

2. Показ компьютерных демонстраций

Модель 1. Опыт Юнга.

Компьютерная модель является аналогом интерференционного опыта Юнга. Можно изменять длину световой волны λ и расстояние между щелями d. На дисплее возникает в увеличенном масштабе интерференционная картина и распределение интенсивности на экране. Рис.11

В нижнем окне высвечиваются значения угла ψ сходимости лучей на экране и ширина интерференционных полос.

Модель 2. Кольца Ньютона.

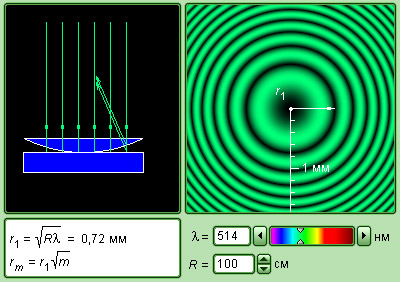Компьютерный эксперимент является аналогом интерференционного опята Ньютона. Можно изменять длину волны λ света и радиус кривизны R поверхности линзы. На экране возникает в увеличенном масштабе картина колец Ньютона и высвечивается значение радиуса r₁ первого темного кольца.

Рис.12

Учебно-методические материалы

Основная литература

1. Савельев И. В. Курс общей физики, кн. 3. – М.: ООО «Издательство Астрель», ООО «Издательство АСТ», 2004, §§ 4.1-4.5

2. Иродов И. Е. Волновые процессы. Основные законы: Учебное пособие для вузов. – М.: Бином. Лаборатория базовых знаний, 2007, §§4.1 - 4.6.

Дополнительная литература

3. Сивухин Д.В. Общий курс физики. т. 4. М.: ФИЗМАТЛИТ, 2009, §§26-28, 37.

4. Ландсберг Г.С. Оптика. -М.,: ФИЗМАТЛИТ, 2003, §11.

5. Лосев В.В. Оптические явления. Теория и эксперимент. Учебное пособие, М., 2002, §§2.1 - 2.6.

Информационно-справочные ресурсы

6. [Электронный ресурс].-М.: Коллекция электронных ресурсов МИЭТ, 2007.- Режим доступа: http://orioks.miet.ru/oroks-miet/srs.shtml

7. Программа обучения. «Открытая Физика 2.6. Часть 2»:

http://www.physics.ru/

http://www.physics.ru/courses/op25part2/design/index.htm

8. Scientific Center «PHYSICON»: of the course «Wave Optics on the Computer»

http://college.ru/WaveOptics/content/chapter1/section1/paragraph1/theory.html

9. Диск или программа «Физика в анимациях»

http://physics.nad.ru/

http://physics.nad.ru/Physics/Cyrillic/optics.htm