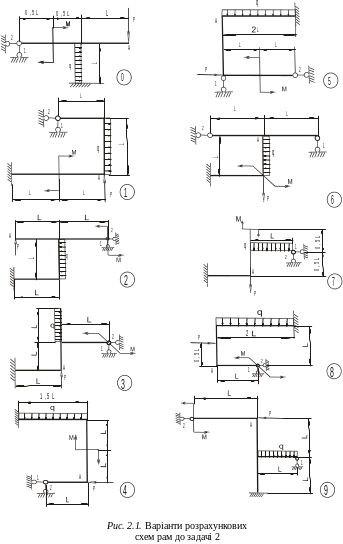
Задача 2 Статично невизначувана рама

Для заданої рами (рис.2.1, табл. 2.1) підібрати двотавровий переріз і визначити переміщення перерізу А. Взяти , . З двох зв’язків 1 та 2 залишити той, що вказаний в табл. 2.1.

Таблиця 2.1. Варіанти завдань до задачі 2

Варіант	Q кН/м	Р кН	М кНм	Переміщення	Матеріал	N зв’язку
0	10	–30	40	wA верт	Сталь25	2
1	–15	25	35	wA гор	Сталь30	1
2	20	–20	30	θA	Сталь40	2
3	25	15	–25	θA	Сталь35	1
4	–10	30	20	wA гор	Сталь50	2
5	15	25	–20	wA верт	Сталь55	1
6	20	–10	40	θA	Сталь50Г	1
7	25	20	–35	θA	Сталь10	2
8	30	10	–30	wA верт	Сталь60	2
9	–30	20	25	wA гор	Сталь30Г	1

План розв’язування задачі

1. Розкрити статичну невизначуваність рами, користуючись канонічними рівняннями методу сил. Для цього необхідно:

– відкинувши зайвий зв’язок, побудувати найбільш раціональний варіант основної системи;

– завантаживши основну систему заданим навантаженням і зайвим зусиллям Х₁, що замінює дію зайвого зв’язку, побудувати еквівалентну систему;

– записати канонічне рівняння методу сил;

– завантажити основну систему по черзі заданим навантаженням і одиничною силою і записати вирази для згинальних моментів від заданих сил та одиничної сили (при використанні способу

Верещагіна побудувати відповідні епюри), обчислити коефіцієнт та вільний член канонічного рівняння за формулами Мора або Верещагіна;

– розв’язати канонічне рівняння і визначити невідоме зусилля Х₁;

2. Побудувати епюру згинальних моментів М для еквівалентної системи.

3. Перевірити правильність розкриття статичної невизначуваності системи, переконавшись за допомогою метода Мора або Верещагіна, що переміщення в напрямку сили Х₁ дорівнює нулю.

4. З умови міцності на згин підібрати двотавровий переріз.

5. Визначити вказане переміщення перерізу А методом Мора або Верещагіна.

Розв’язання задачі

Підібрати двотавровий переріз для рами, показаної на рис. 2.2, а, та визначити кут повороту перерізу А. При цьому для всієї рами, матеріал рами – сталь 20, для якої допустиме напруження на розтяг .

Рама один раз статично невизначувана. Основну систему виберемо, відкинувши зайвий зв'язок – шарнірно-рухому опору (рис. 2.2, б). Завантаживши основну систему заданим навантаженням та зайвою невідомою силою Х₁, яка замінює дію відкинутого зв’язку, отримаємо еквівалентну систему (рис. 2.2, в).

Канонічне рівняння методу сил для один раз статично невизначуваної рами має вигляд:

, звідки .

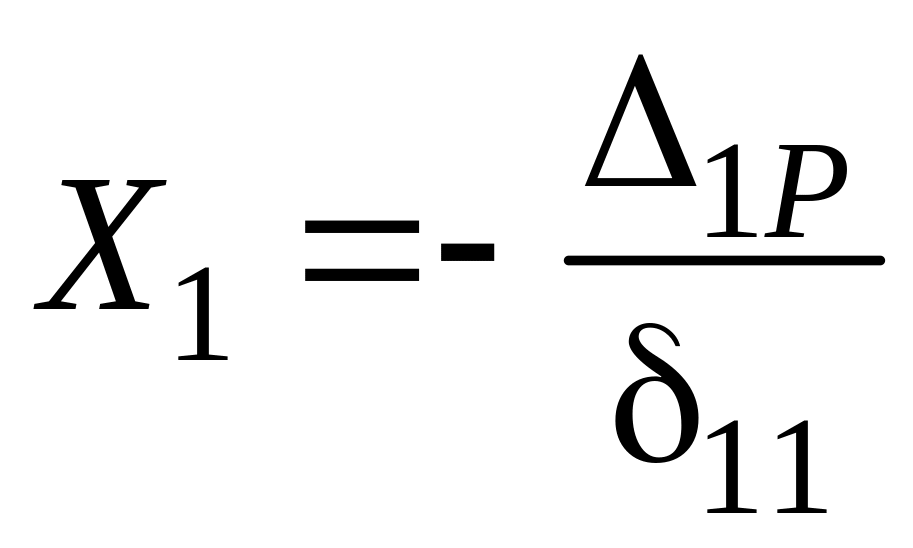Отже, щоб визначити зайву невідому силу Х₁, треба попередньо обчислити коефіцієнт та вільний член . Їх визначимо методом Верещагіна. Для цього основну систему завантажуємо заданим зовнішнім навантаженням і записуємо вирази для згинальних моментів від заданих сил

q

на кожній ділянці (рис. 2.2, г):

ділянка І : ;

ділянка IІ : ;

ділянка IIІ : ;

ділянка ІV : .

Будуємо епюру згинальних моментів (рис. 2.2, д).

Для одиничної системи (рис. 2.2, е):

ділянка І : ;

ділянка IІ : ;

ділянка IIІ : ;

ділянка ІV : .

За цими даними побудуємо епюру згинальних моментів (рис. 2.2, е).

За допомогою епюр та обчислимо коефіцієнт та вільний член канонічного рівняння методу сил:

,

.

Таким чином, .

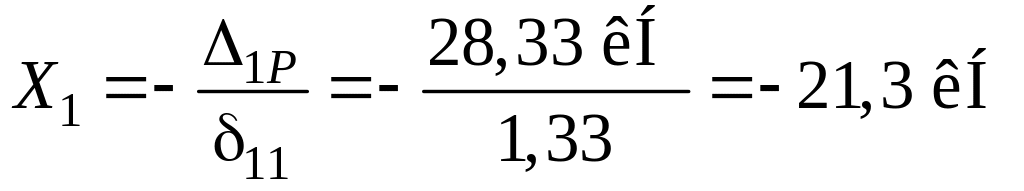Отже задана рама навантажена, як показано на рис. 2.2, ж.

2. Будуємо епюру згинальних моментів М для еквівалентної системи, записавши спочатку вирази для згинальних моментів М на кожній ділянці:

ділянка І : ;

ділянка IІ : ;

ділянка IIІ : ;

ділянка ІV : .

Е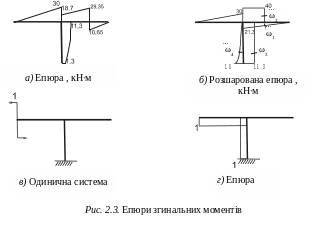 пюра згинальних моментів М для цього випадку представлена на рис. 2.3, а.

3. Перевіримо правильність розкриття статичної невизначуваності рами. З цією метою обчислимо переміщення перерізу В в напрямку сили Х₁ за методом Верещагіна, враховуючи попередньо побудовані епюри згинальних моментів М (рис. 2.3, а) та (рис. 2.2, є).

На рис. 2.3, б показано розшаровану епюру М на ІІ, ІІІ, ІV ділянках:

ω₁ – площа епюри М на ІІ і ІІІ ділянках від ;

ω₂ – площа епюри М на ІІІ ділянці від ;

ω₃ – площа епюри М на ІV ділянці від , та ;

ω₄ – площа епюри М на ІV ділянці від .

Шукане переміщення:

В зв’язку з тим, що при розкритті статичної невизначуваності системи зайві невідомі визначаються з окресленою точністю, наслідки перевірки мають також похибку – шукані переміщення відрізняються від нуля. Тому при перевірці рекомендується окремо обчислювати суму додатних та від’ємних членів. Якщо виражене у відсотках відношення різниці між цими сумами до меншої з них невелике (до 5 %), то результат можна вважати задовільним.

В нашому випадку

,

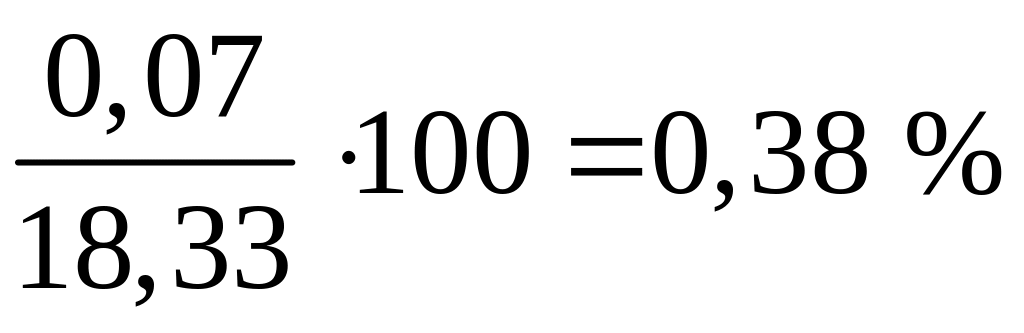отже статична невизначуваність рами розкрита правильно.

4. Підберемо двотавровий переріз для еквівалентної системи, тобто для заданої рами з умови міцності рами:

, звідси .

З епюри згинальних моментів для еквівалентної системи (рис. 2.3) витікає, що .

Тому момент опору двотаврового перерізу:

.

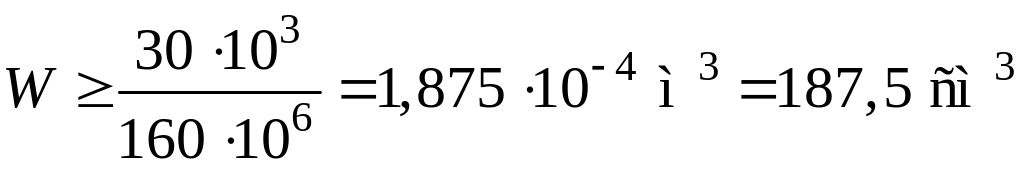Орієнтуючись на цей результат, вибираємо двотавр № 20a, для якого

, .

5. На цьому етапі розрахунку визначимо кут повороту перерізу А методом Верещягіна (або Мора). У зв’язку з цим розглянемо одиничну систему, тобто випадок, коли основна система в перерізі А завантажується одиничним моментом (рис. 2.3, в).

При цьому вирази для згинальних моментів на ділянках мають вигляд:

ділянки І і ІV: ;

ділянки IІ і IIІ: .

Кут повороту перерізу A рами:

.

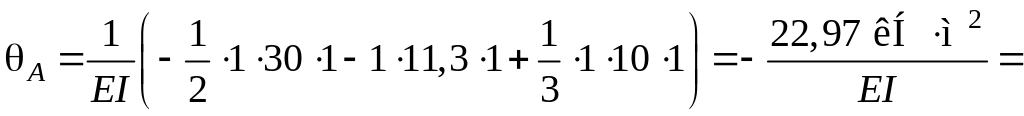
Від’ємний знак означає, що переріз A повертається у протилежному по відношенню до одиничного моменту, що прикладений в цьому перерізі, напрямку, тобто за годинниковою стрілкою.