Задача 12 розрахунок тонкостінної посудини на опорах

Сталеву тонкостінну циліндричну посудину з днищами встановлено на чотирьох симетрично розташованих опорах (рис.12.1, табл.12.1). Посудина знаходиться під внутрішнім тиском p і заповнена на 2/3 висоти Н рідиною з питомою вагою . Обчислити товщину стінки посудини в небезпечному перерізі. Допустиме напруження на розтяг для матеріалу посудини . Підібрати переріз стояків з умови стійкості. Прийняти для стояків , , , .

Таблиця 12.1. Варіанти завдань до задачі 12

Варіант	p, МПа	, кН/м3	Н, м	h, м	R, м	L, м	Перерізи стояка
0	1,5	20	4,5	1,3	1,3	2,5
1	1,2	30	3,5	1,0	1,2	2,2
2	2,1	35	3,0	0,8	1,0	1,8
3	1,9	25	3,6	0,6	1,1	2,0
4	1,6	30	3,5	0,5	0,9	1,9
5	1,8	40	2,8	0,7	0,8	2,0
6	1,4	25	4,0	1,1	1,1	3,0
7	2,0	20	3,8	0,9	1,0	2,5
8	1,7	40	2,6	0,5	0,6	2,1
9	1,3	25	4	1,2	1,3	2,4

Рис. 12.1. Варіанти схем посудин до задачі 12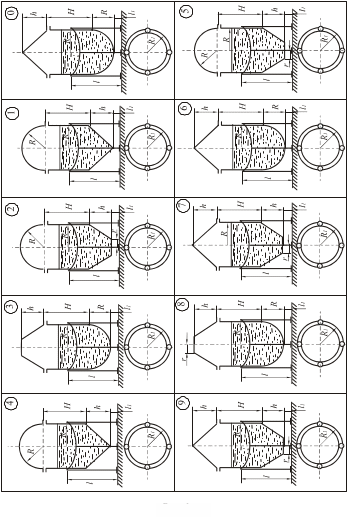

План розв’язування задачі

1. Обчислити товщину стiнки посудини в небезпечному перерiзi.

2. Визначити навантаження на стояк, враховуючи вагу рiдини, самої оболонки та її днищ.

3. Підібрати перерiз стояка з розрахунку на стiйкiсть, вважаючи стояк на одному кiнцi (верхньому) закрiплений шарнiрно, на другому – жорстко.

Розв’язання задачі

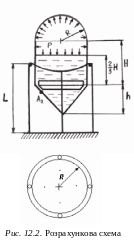
Дано: , ,

, , , ,

, переріз стояків – [] (2 швелери),

, .

Обчислити: 1) – товщину стінки оболонки (з розрахунку на міцність посудини),

2) номер швелера (з розрахунку на стійкість стояків).

1. Розрахуємо на міцність циліндричну частину посудини.

Меридіональний та коловий радіуси:

; .

Тиск на поверхню циліндра в залежності від глибини:

.

Рівняння рівноваги зони (рис. 12.3):

.

З відси

.

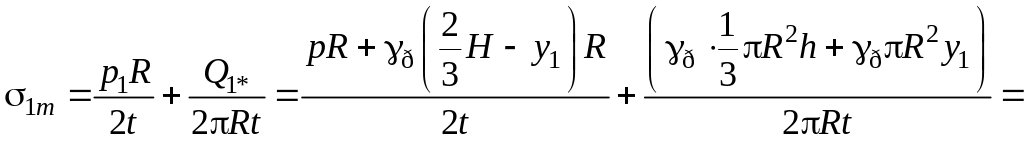
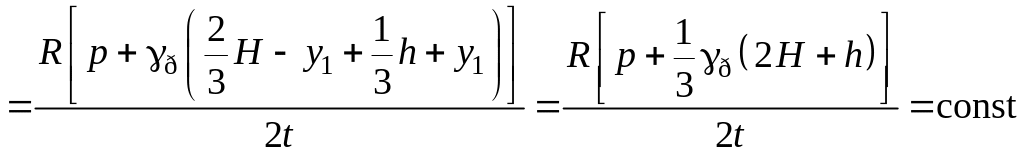Рівняння Лапласа

,

звідси виходить

.

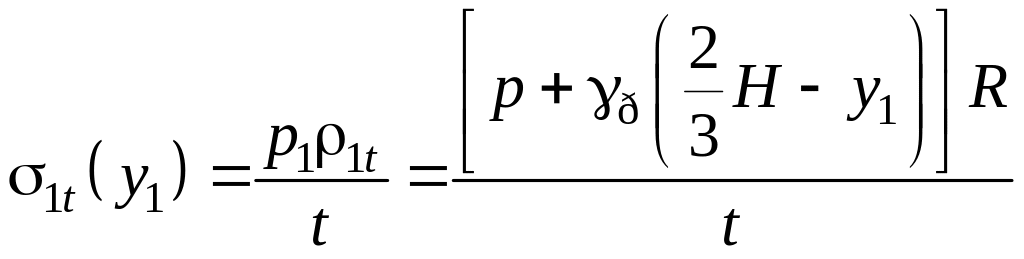Небезпечні точки, де найбільші напруження, – це точки циліндра на рівні А₁, напруження в них:

,

.

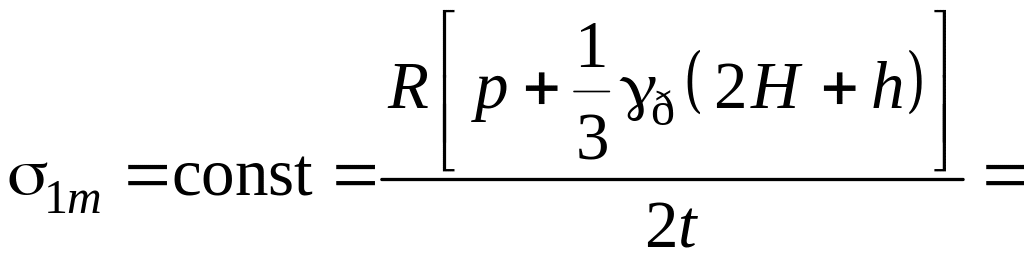
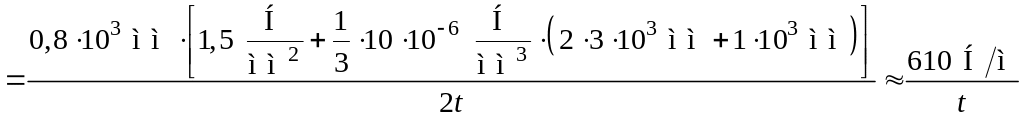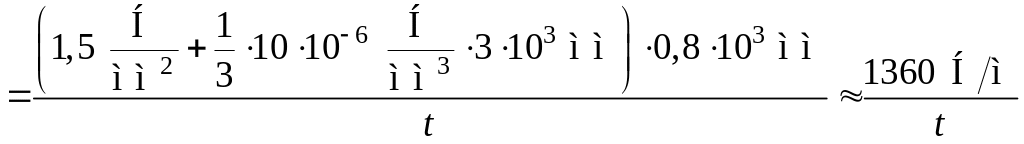Умова міцності для небезпечних точок А₁ за ΙV критерієм міцності:

.

Звідси

.

2. Розрахуємо на міцність конічну частину посудини.

Для конічної частини (рис. 12.4):

, .

y₂

p₂

,

,

,

.

,

.

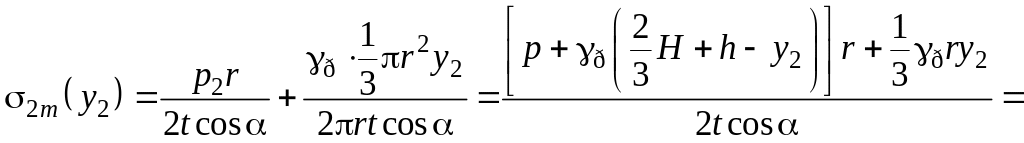
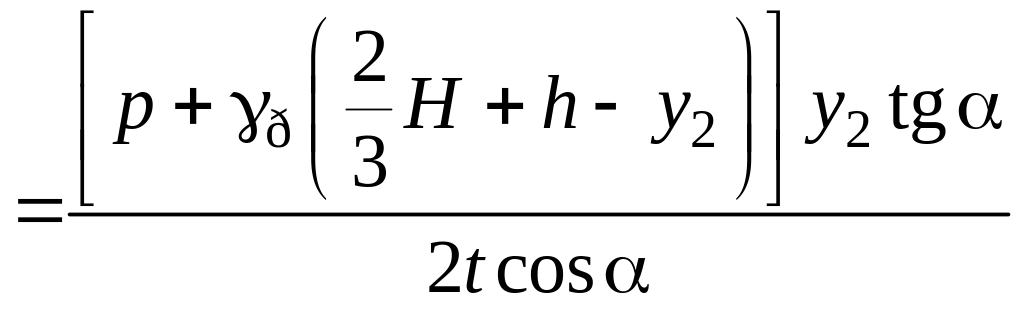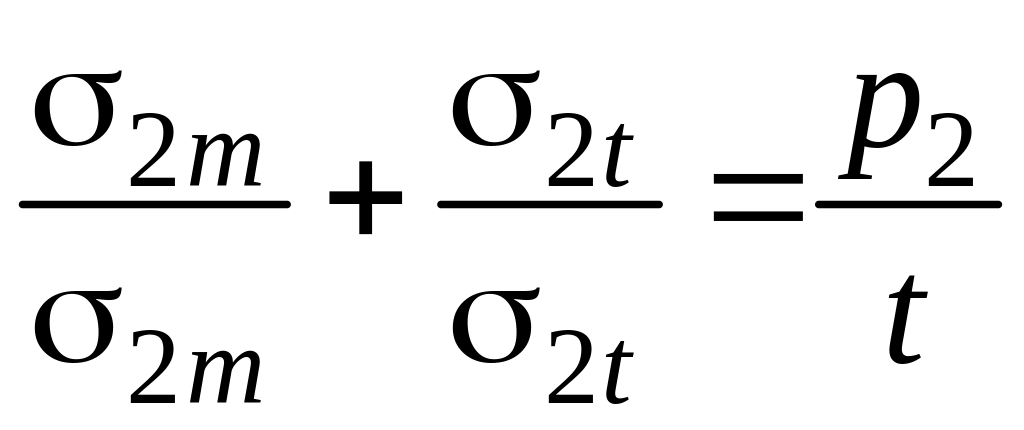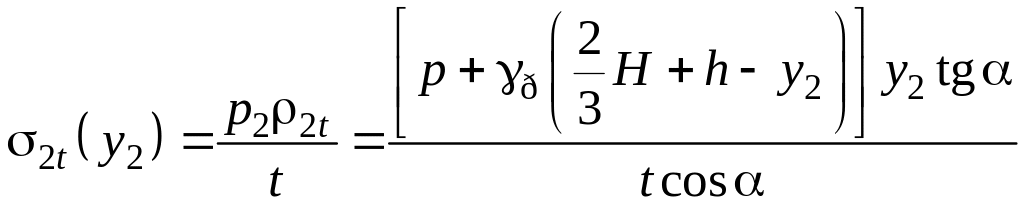Знайдем координати точок конуса, в яких напруження найбільші:

,

.

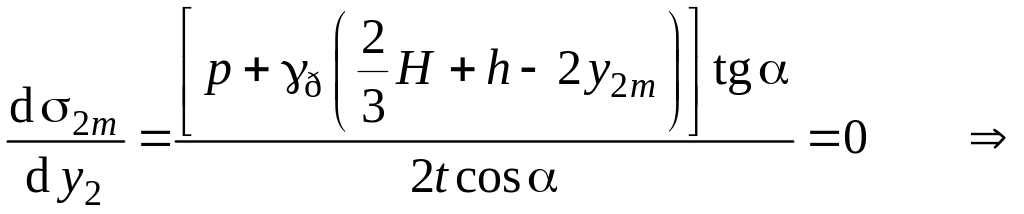
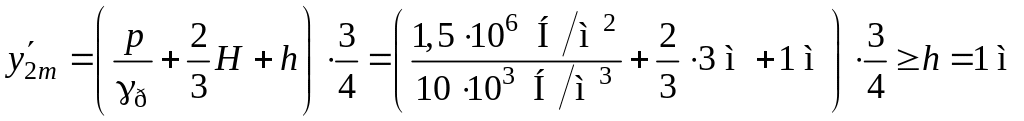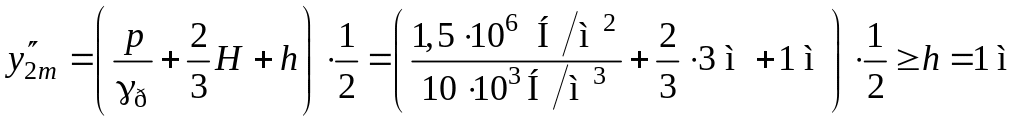Обидві точки знаходяться вище конуса висотою h. Отже небезпечні точки конуса А₂ знаходятся у верхній частині конуса. Напруження в них ( ):

,

.

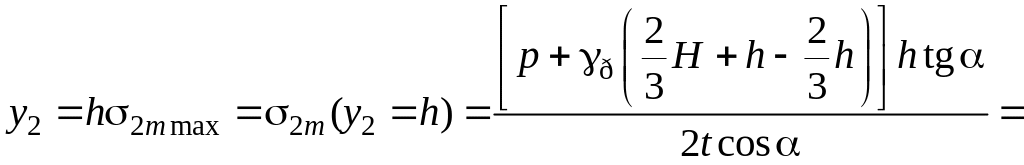
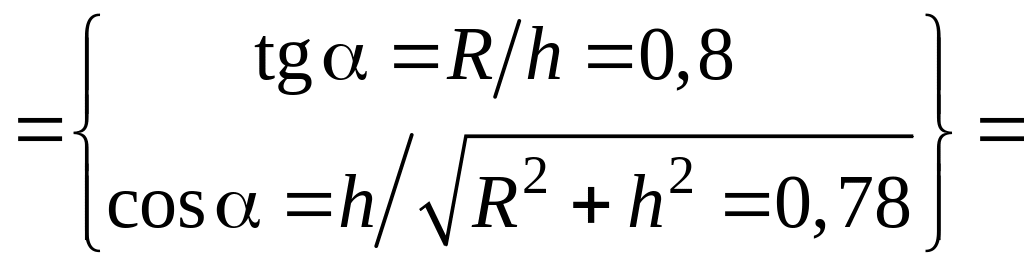
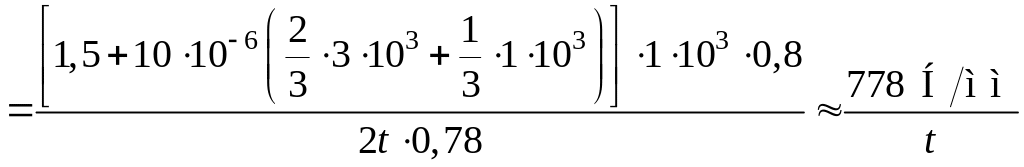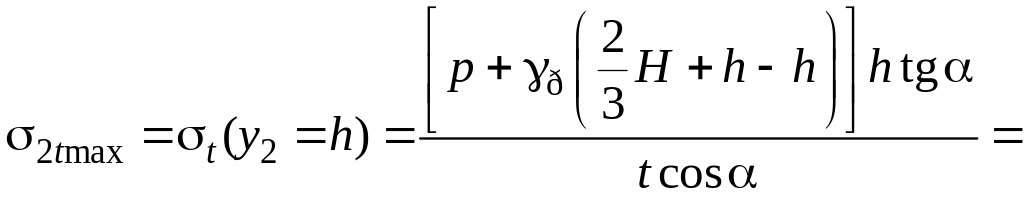
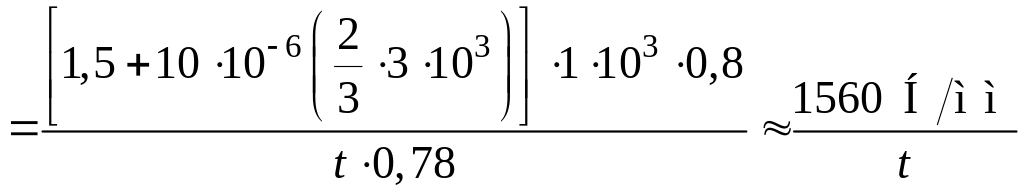Умова міцності конічної частини:

.

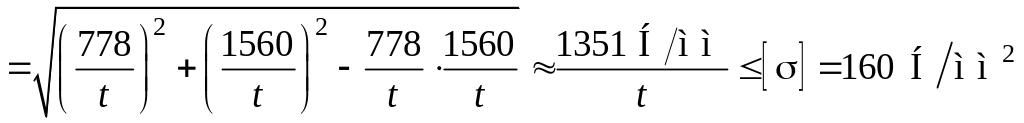Звідси

.

Посудина буде міцною, якщо і циліндрична, і конічна її частини будуть міцні. Таким чином, умова міцності посудини – система нерівностей:

Обираємо .

3. Визначимо навантаження на стояк.

В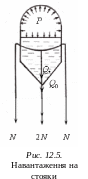 рахуємо вагу посудини – оболонки та рідини в посудині. Рівняння рівноваги посудини з рідиною (рис. 2.5):

.

Зусилля в стояку:

.

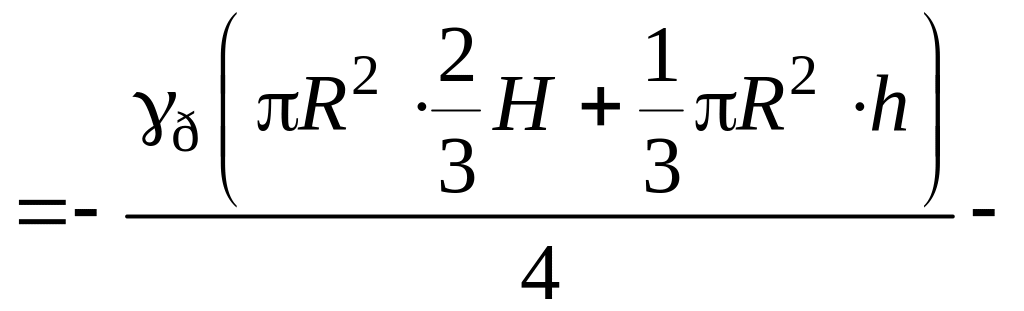
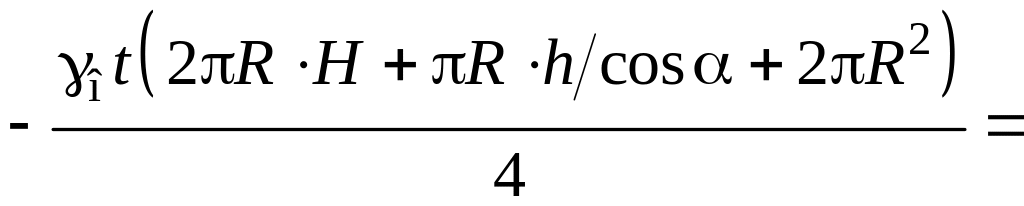
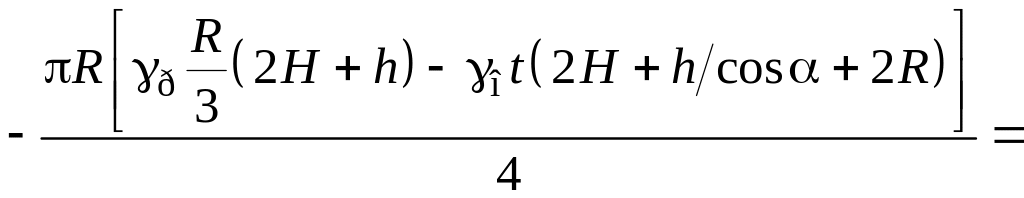
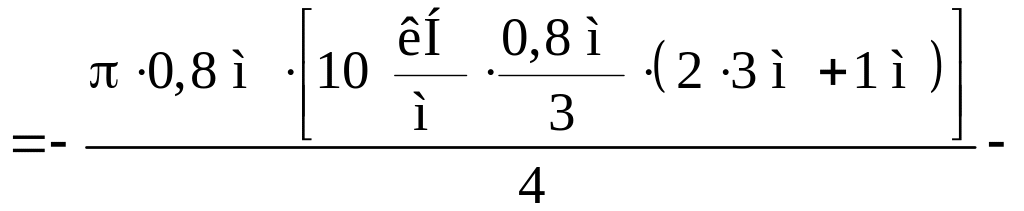
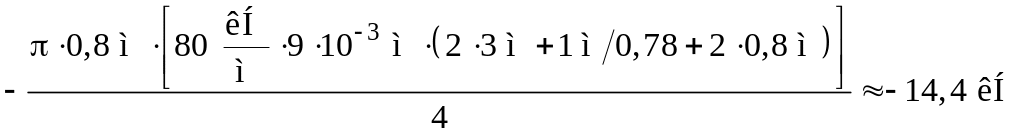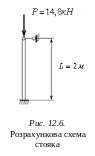
4. Розрахуємо стояк на стійкість за допомогою метода послідовних наближень (рис. 12.6):

1-е наближення: .

.

.

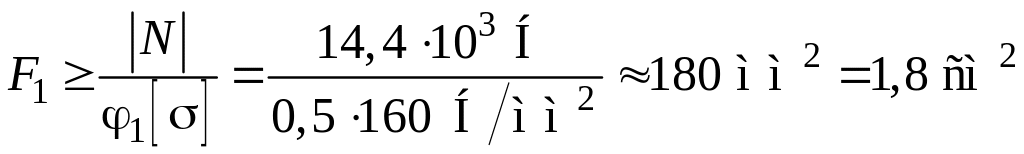
Вибираємо швелер № 5 (найменший швелер в сортаменті): ; ;

; .

Для двох швелерів № 5 (рис. 12.7):

; .

Радіус інерції

.

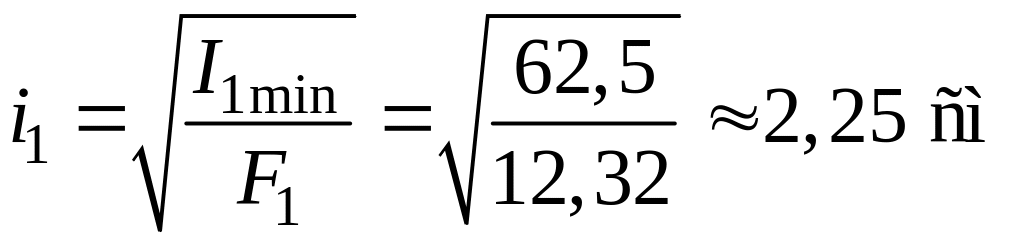Гнучкість стояка

.

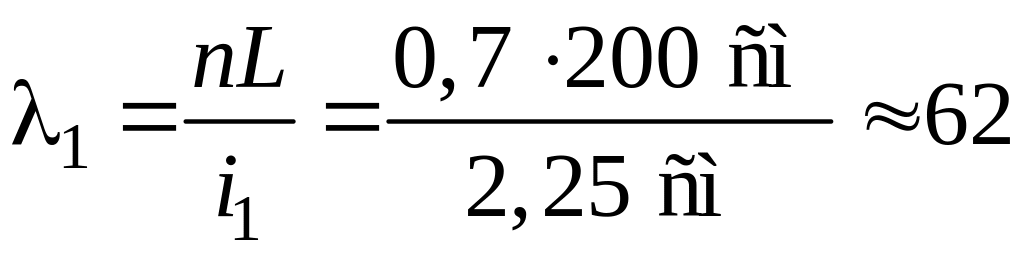Уточненний коефіцієнт φ: .

Різниця

.

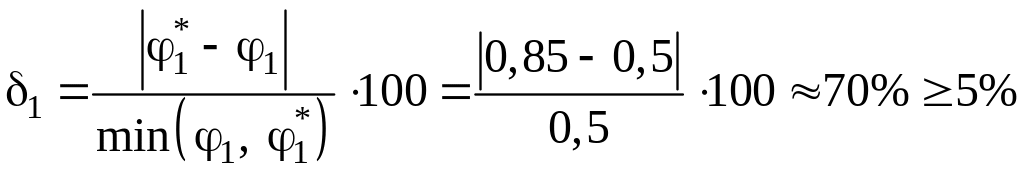2-е наближення: .

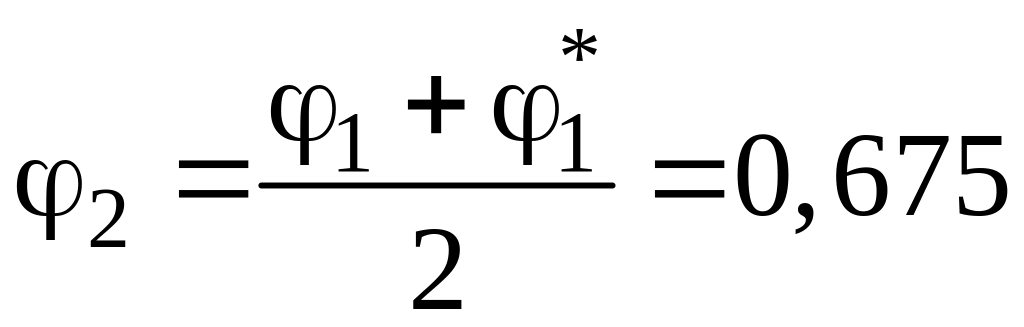Далі за вищенаведеними формулами одержимо:

.

Залишаємо найменший швелер № 5 з сортаменту. У цьому випадку, як було розраховано вище,

.

Різниця

.

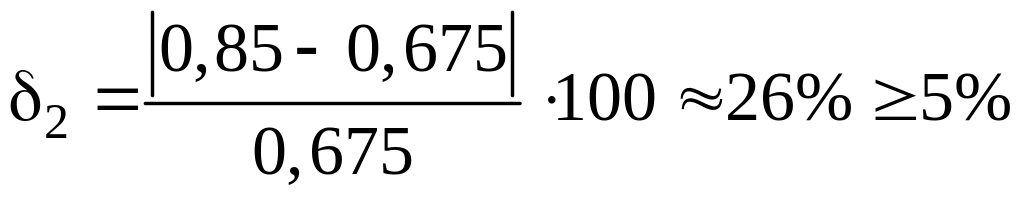Очевидно, в подальших наближеннях необхідна площа швелера буде зменшуватися. Тому остаточно вибираємо для стояка 2 швелери № 5.

Перевіримо виконання умови стійкості стояка:

.

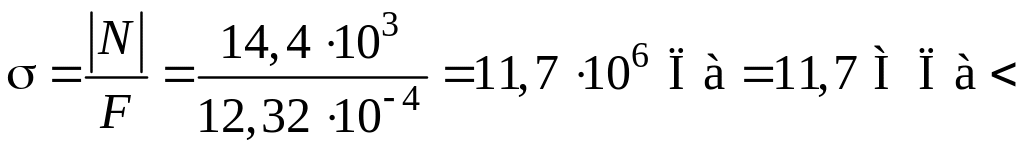
Стояки за умовою стійкості значно недовантажено.