
- •Проектирование дискретной системы передачи данных
- •2 Основная часть
- •2.1 Постановка задачи
- •3 Статистический анализ искажений
- •3.1 Прове рка соответствия закона распределения имеющимся статистическим данным
- •4 Вероятность искажений заданной величины
- •5 Исправляющая способность приёмника
- •6 Определение вероятности ошибок к ратностей 1, 2, 3 для заданного сообщения
- •7 Выбор способа повышения верности передачи заданного сообщения
- •8 Определение количества блоков в передаваемом сообщении, выбор параметров помехоустойчивого кода
- •9 Структура пакета данных
- •10 Составление алгоритмов функционирования передающего
- •11Составление схемы кодирующего и декодирующего устройств для обнаружения ошибок
- •12 Характеристики раз работанной системы
4 Вероятность искажений заданной величины
При распределении
искажений по нормальному закону
вероятность ошибки численно равна
вероятности появления искажения,
превышающего допустимое значение
 .
.
Необходимо
определить вероятность превышения
случайной величиной некоторого значения
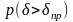 (в данном курсовом проекте по заданию
– вероятность превышения 0,2; 0,35; 0,4 и
0,47. Это необходимо осуществить с учётом
преобладаний, которые связаны с индексом
модуляции и девиации. То есть нужно
оценивать такие искажения с учётом
возможности сдвигов.
(в данном курсовом проекте по заданию
– вероятность превышения 0,2; 0,35; 0,4 и
0,47. Это необходимо осуществить с учётом
преобладаний, которые связаны с индексом
модуляции и девиации. То есть нужно
оценивать такие искажения с учётом
возможности сдвигов.
Согласно
заданию

Вероятность превышения определится как:

где
 – функция Лапласа (вероятностей)
аргумента Z,
– функция Лапласа (вероятностей)
аргумента Z,
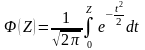
 – величина
преобладания отклонения вправо или
влево (так же является случайной
величиной):
– величина
преобладания отклонения вправо или
влево (так же является случайной
величиной):
 ,
,
 Значение функции Лапласа можно
найти по соответствующим таблицам или
при помощи математических приложений
для ПК (в данном случае использовался
пакет MathCAD). Ход расчетов и их результаты
сведены в таблицу 3.
Значение функции Лапласа можно
найти по соответствующим таблицам или
при помощи математических приложений
для ПК (в данном случае использовался
пакет MathCAD). Ход расчетов и их результаты
сведены в таблицу 3.
Таблица 3
|
|
|
|
|
|
20 |
-3.047061979 |
1.326349429 |
0,49884455 |
0,407638009 |
0,093517441 |
35 |
-4.687091256 |
2.966378706 |
0,499998614 |
0,498493354 |
0,001508032 |
40 |
-5.233767682 |
3.513055132 |
0,499999917 |
0,499778507 |
0,000221576 |
47 |
-5,999114678 |
4,278402128 |
0,499999999 |
0,499990588 |
9,41298E-06 |
Значение функции Лапласа и были найдены при помощи программного пакета математического моделирования MathCAD.
Очевидно, что
для соблюдения требований МСЭ-Т, которые
регламентирую величину ошибки не хуже,
чем
 ,
следует выбрать допустимое отклонение
равным 47%. Таким образом,
,
следует выбрать допустимое отклонение
равным 47%. Таким образом,
 .
.
5 Исправляющая способность приёмника
Одним из основных параметров приемника дискретной информации характеризующим помехоустойчивость является исправляющая способность.
На основе результатов предыдущего пункта полагаем, что исправляющая способность регистрирующего устройства будет определяться величиной 45%.
Рассчитаем при этом интервал регистрации:

где
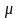 –
относительная величина краевых
искажений,
–
относительная величина краевых
искажений,
 –
длительность элементарного импульса,
с;
–
длительность элементарного импульса,
с;
где В - скорость дискретной модуляции, Бод (19*200=3800 Бод);
 –
интервал (время) регистрации, при котором
еще не возникает ошибки, с;
–
интервал (время) регистрации, при котором
еще не возникает ошибки, с;

Таким образом,
интервал регистрации для премного
устройства должен соответствовать
примерно
 секунды.
секунды.
6 Определение вероятности ошибок к ратностей 1, 2, 3 для заданного сообщения
V=7600 байт, имени, фамилии, отчества.
Необходимо определить вероятности появления ошибок кратностей 1,2 и 3 в следующем сообщениях:
[Хасанов], [Алексей], [Анатольевич], [7600].
Вероятности рассчитаем, используя формулу Бернулли:
 ,
,
 ,
,
Где
 –
нормативная вероятность появления
ошибки в одном элементе данных,
–
нормативная вероятность появления
ошибки в одном элементе данных,
 ;
;
 –
кратность ошибки;
–
кратность ошибки;
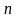 –
число элементов в посылке (сообщении).
–
число элементов в посылке (сообщении).
Используется
код КОИ-7, соответственно имеем, что
 =8.
=8.
Таблица 4
|
Хасанов |
Nобщ= |
56 |
Сn |
Pn(1)= |
5,26854E-04 |
|
56 |
|
Pn(2)= |
1,36381E-07 |
1540 |
||
Pn(3)= |
2,31078E-11 |
27720 |
||
Таблица 5
|
Алексей |
Nобщ= |
56 |
Cn |
Pn(1)= |
5,26854E-04 |
|
56 |
|
Pn(2)= |
1,36381E-07 |
1540 |
||
Pn(3)= |
2,31078E-11 |
27720 |
||
Таблица 6
|
Анатольевич |
Nобщ= |
88 |
Cn |
Pn(1)= |
8,27664E-04 |
|
88 |
|
Pn(2)= |
3,38902E-07 |
3828 |
||
Pn(3)= |
9,14498E-11 |
109736 |
||
Таблица 7
|
7600 |
Nобщ= |
60800 |
Cn= |
Pn(1)= |
4,92630E-01 |
|
60800 |
|
Pn(2)= |
1,40967E-01 |
1848289600 |
||
Pn(3)= |
4,31921E-07 |
601623295 |
||






