2.7 Применение задачи о назначениях к решению экономических проблем
Выше уже был дан пример применения задачи о назначениях к проблеме оптимального выбора руководителей исследовательских проектов. Приведем еще несколько примеров, когда использование задачи о назначениях позволяет найти оптимальное решение экономической задачи.
Оптимальное исследование рынка.
Группе, исследующей
рынок, требуется получить данные из
различных мест. В ее распоряжении имеется
дней, и она предполагает провести по
одному дню в каждом месте, проведя по
опросов,
.
Вероятность успешного опроса в каждом
месте задается матрицей
.
Элемент матрицы
характеризует вероятность успешного
опроса в течение
-го
дня в
-м
месте,
.
Определить время проведения опросов, при котором общее число опросов максимально.
Решение.
Сведем данную задачу к задаче о назначениях.
Введем величину
,
показывающую число успешных опросов в
-м
месте в течение
-го
дня.
Математическая модель задачи имеет следующий вид:
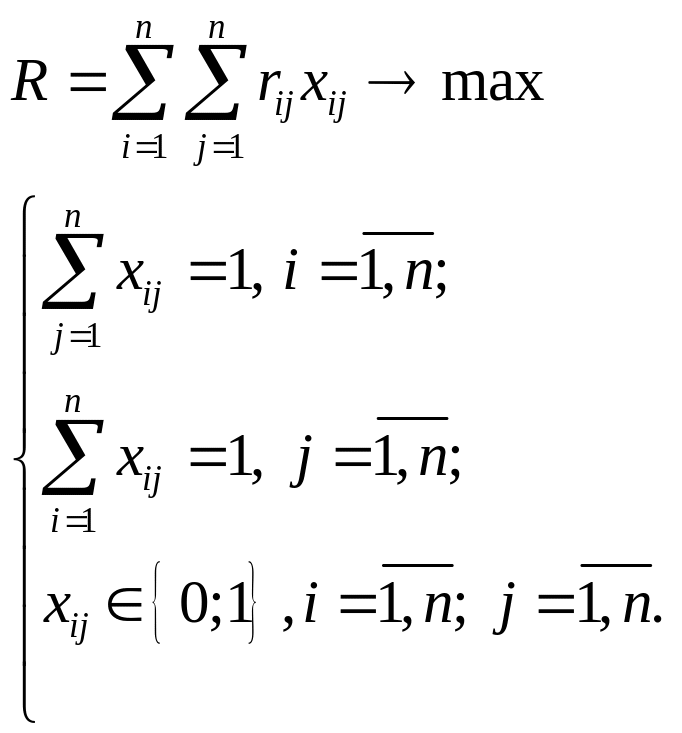
Функция
характеризует суммарное число опросов.
Его нужно максимизировать. Первое и
второе ограничения соответствуют тому,
что в течение одного дня можно находиться
только в одном месте. Для расчета модели
венгерским методом надо перейти к
противоположной функции:
и в соответствующей
таблице записывать значения
с противоположным знаком.
Оптимальное использование торговых агентов.
Торговая фирма
продает товары в
различных городах, покупательная
способность жителей которых оценивается
в
усл. ед.,
.
Для реализации товаров фирма располагает
торговыми агентами, каждого из которых
она направляет в один из городов.
Профессиональный уровень агентов
различен; доля реализуемых
-м
торговым агентом покупательных
способностей составляет
.
Как следует распределить торговых
агентов по городам, чтобы фирма получила
максимальную выручку от продажи товаров?
Решение.
Оптимальное решение этой проблемы может быть найдено с помощью задачи о назначениях. В качестве кандидатов выступают торговые агенты, в качестве работ — города.
Введем параметр
,
характеризующий величину покупательных
способностей, реализуемых
-м
торговым агентом в
-м
городе.
Управляющие
переменные
определяются по формуле
Математическая модель запишется в следующей форме:
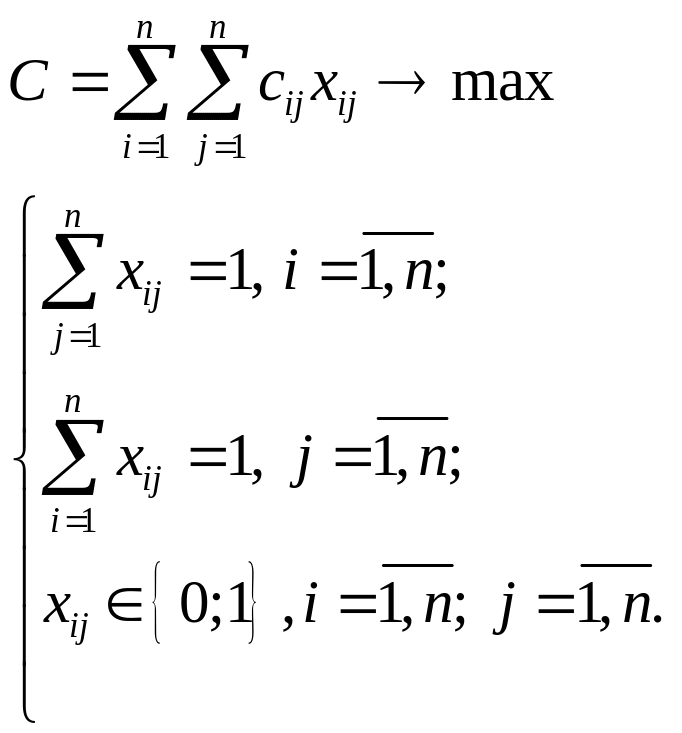
Первое и второе ограничения формализуют соответственно о том, что в каждый город направляется один торговый агент, и один торговый агент не может работать в двух городах. Целевая функция — это сумма реализованных покупательных способностей всеми торговыми агентами во всех городах. Она должна быть максимальна. Для решения задачи венгерским методом надо, как и в предыдущем примере, перейти к противоположной функции.
Заключение
В данной работе рассмотрены математические модели оптимизации ресурсов, конкретно, линейные, как наиболее изученные и распространенные. Рассмотрена задача линейного программирования в общем виде, даны алгоритмы решения ЗЛП графическим и симплекс-методом, дана экономическая интерпретация двойственным задачам, описано решение задачи целочисленного программирования методом Гомори. Во второй главе раскрыты специальные задачи линейного программирования, в том числе транспортная задача и задача о назначениях, описано составление начального плана для транспортной задачи различными методами, нахождение оптимального плана для транспортной задачи методом потенциалов, рассмотрена задача о назначениях и ее решение венгерским методом. В курсовой работе приведены примеры с подробным решением.
Список литературы