3.2. Проведем предварительную обработку данных.

Выборочное среднее в каждом опыте (см. уравнение (8)):

, .

Например, выборочное среднее в третьем опыте ( ):

.

Выборочная дисперсия в каждом опыте (см. уравнение (9)):

, .

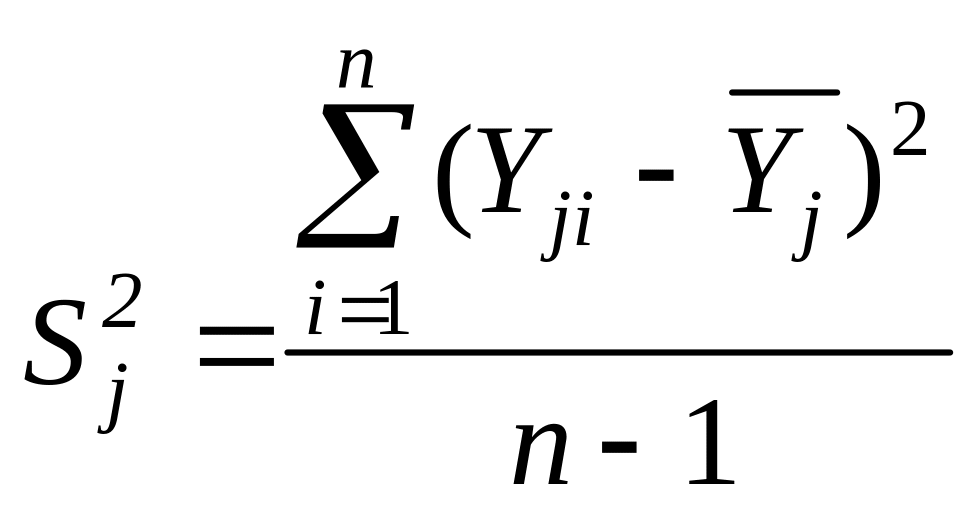Например, выборочная дисперсия в третьем опыте ( ):

.

Проверка на однородность выборочных дисперсий по критерию Кохрена (см. уравнения (10)):

‑ экспериментальное значение критерия Кохрена G_э :

;

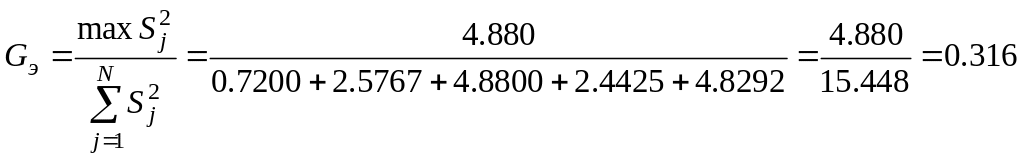‑ табличное значение критерия Кохрена  при , и доверительной вероятности р = 0.95 выбирается из таблицы Приложения 5:

.

Вывод: выборочные дисперсии однородны, так как (см. уравнение (11)).

Дисперсия воспроизводимости и её число степеней свободы (см. уравнение (13) – (14)):

,

.

4. Создадим матрицу моделирования на базе РСП для , проведём окончательную обработку экспериментальных данных для построения однофакторного уравнения регрессии первого порядка (см. раздел А, п. 5) (все окончательные результаты расчётов внесём в таблицу 4).

4.1. Создадим столбец нормированного фактора , все значения которого равны .

4.2. Столбец нормированных фактора перенесём из таблицы 3 в таблицу 4.

Таблица 4. – Матрица моделирования для построения однофакторного уравнения регрессии первого порядка на базе РСП для и результаты окончательной обработки экспериментальных данных

N	X0j	X1j
1	1	–1.0	74.10	74.10	– 74.10	68.50	31.36
2	1	–0.5	61.45	61.45	– 30.73	64.85	11.56
3	1	0.0	57.00	57.00	0.00	61.20	17.64
4	1	0.5	54.13	54.13	27.07	57.55	11.70
5	1	1.0	59.48	59.48	59.48	53.90	31.14
	5	2.500		306.2	‑ 18.28
				61.2	‑ 7.3	;
Уравнение неадекватно				1.2	1.7

4.3. Рассчитаем суммы квадратов столбцов и :

4.4 Образуем вспомогательные столбцы и рассчитаем их суммы:

,

.

4.5. Рассчитаем по уравнениям (15) – (16)) коэффициенты для построения однофакторного уравнения регрессии первого порядка :

,

.

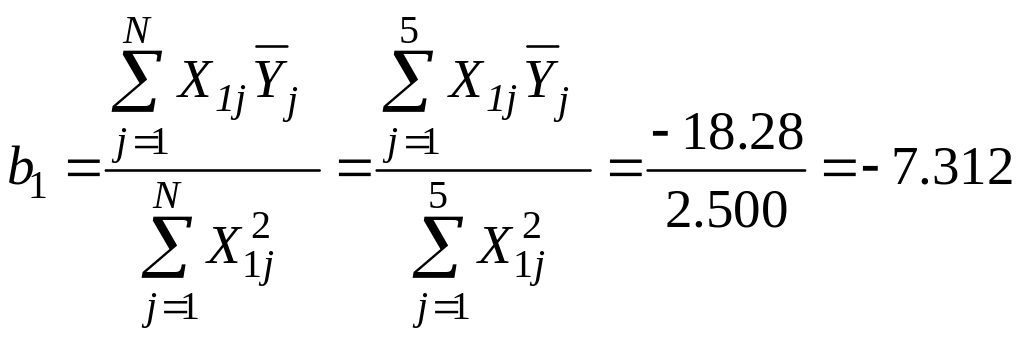5. Произведем статистическую оценку качества полученного однофакторного уравнения первого порядка.

5.1. Проверим коэффициенты b₀, b₁ на значимость по критерию Стьюдента.

Рассчитаем дисперсии значимости , (см. уравнения (17) ‑ (18)):

,

;

,

.

Рассчитаем доверительные интервалы коэффициентов b₀, b₁ (см. уравнения (19) ‑ (20)):

;

,

где  ‑ табличное значение критерия Стьюдента при числе степеней свободы и доверительной вероятности выбирается из таблицы Приложения 2.

С учетом доверительных интервалов коэффициенты корректно запишем результат расчёта:

,

.

Регрессионные коэффициенты значимы (см. уравнения (21) ‑ (22)), так как:

, .

Вывод: однофакторное уравнение регрессии первого порядка имеет следующий вид:

.

5.2. Проверим однофакторное уравнение регрессии первого порядка на адекватность по критерию Фишера.

Рассчитаем по однофакторному уравнению регрессии первого порядка значения в каждом опыте. Например, для : .

Образуем столбец и рассчитаем его значения:

Например, для : .

Рассчитаем остаточную сумму квадратов :

Рассчитаем дисперсию адекватности и её число степеней свободы (см. уравнения (23) ‑ (24)):

, .

Проверим полученное однофакторное уравнение регрессии первого порядка на адекватность по критерию Фишера:

‑ экспериментальное значение критерия Фишера F_э (см. уравнения (25)):

, так как ;

‑ табличное значение критерия Фишера при , и доверительной вероятности р = 0.95 выбирается из таблицы Приложения 4:

.

Вывод: полученное однофакторное уравнение регрессии первого порядка неадекватно, так как (см. уравнение (27)).

6. Так как однофакторное уравнение регрессии первого порядка неадекватно перейдем к построению однофакторного уравнения второго порядка.

Ответ: задача 4, вариант 30. Уравнение регрессии первого порядка.

1. Однофакторное уравнение регрессии первого порядка , кВтч/т .

0.8 1.2

Все 5 выборочных дисперсий однородны, так как .

, , , .

Однофакторное уравнение регрессии первого порядка неадекватно, так как:

.

2. Так как однофакторное уравнение регрессии первого порядка неадекватно следует перейти к построению однофакторного уравнения регрессии второго порядка.