Недостаток метода состоит в том, что в оценках содержатся не остатки -го структурно уравнения, а остатки уравнения, полученного на втором этапе,

3. Пример применения 2мнк

Пример. Введем переменные:

- денежное обращение; -денежные доходы населения;

- оборачиваемость денег; - размер вклада в сберегательную кассу.

Данные наблюдений представлены в таблице:

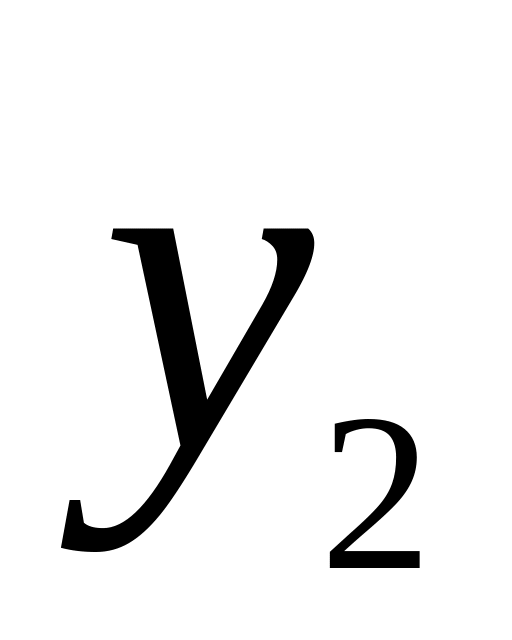
10	14	1	3
13	15	4	4
14	13	3	2
16	11	5	5
20	12	6	2
23	10	6	2
25	8	8	1
24	6	8	4
27	5	9	2
28	6	10	3

Вычислим средние

Перейдем к отклонениям, которые находятся по формулам

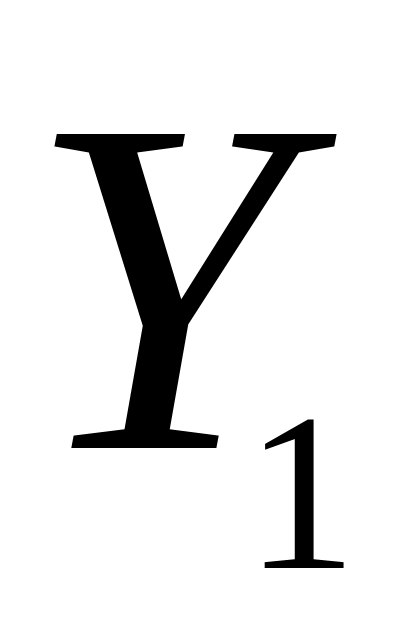
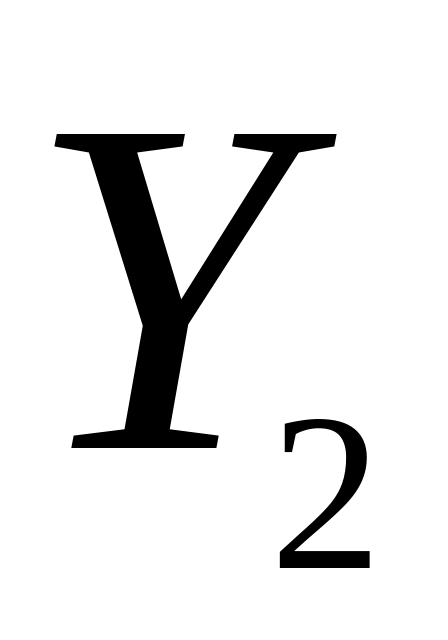
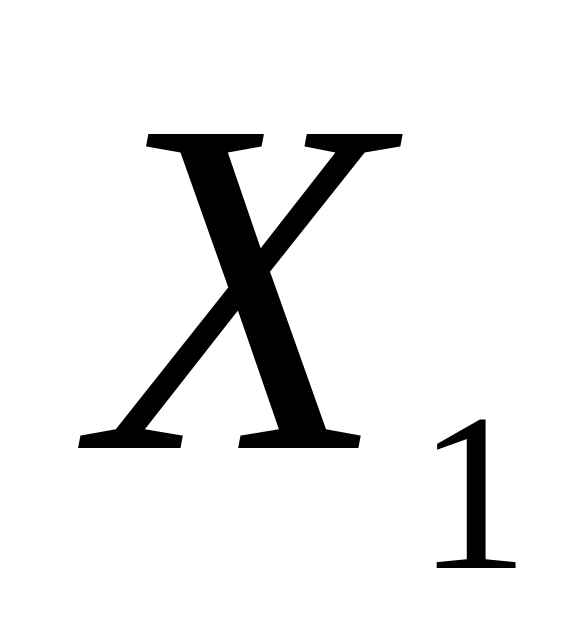
-10	4	-5	1
-7	4	-5	1
-6	3	-3	0
-4	1	-1	3
0	2	0	0
3	0	0	0
5	-2	2	-1
4	-4	2	2
7	-5	3	0
8	-4	4	1

Переменные и необходимо объяснить с помощью модели. Можно записать линейную эконометрическую модель:

(17)

Все переменные представлены в виде отклонений от соответствующих средних. Благодаря этому в обоих уравнениях системы исчезают постоянные регрессии и и система может быть записана в виде

(18)

Приведем корреляционную матрицу, полученную с помощью пакета электронных таблиц EXСEL 7.0:

	1	-0,92464	0,96801	-0,35532
	-0,92464	1	-0,9082	0,176238
	0,969801	-0,9082	1	-0,19174
	-0,35532	0,176238	-0,19174	1

Очевидно наличие мультиколлинеарности между переменными и .

Если провести идентификацию первого уравнения методом наименьших квадратов, не учитывая связи между переменными, то получим не состоятельные оценки для параметров уравнения.

Конкретизируем вначале уравнение (5). В первом уравнении переменная является зависимой, а переменная объясняет ее, поэтому ее можно отнести к числу независимых, которые коррелируют с остальными независимыми переменными. Следовательно, равна вектору , вектору наблюдений над переменной . В первое уравнение включена также другая переменная . Матрица состоит только из вектора наблюдений над переменной . Поэтому полагаем, что . Благодаря этому вектор содержит только параметр . В первом уравнении сдержатся две независимые и некоррелированные между собой переменные и , так что в матрице имеются векторы наблюдений над переменной и над переменной

В соответствии с этим состоит из двух компонент . Вектор становится вектором остатков первого структурного уравнения . Уравнение (5) принимает следующую конкретную форму:

(19)

Матрица представляет собой множество наблюдений над переменными и

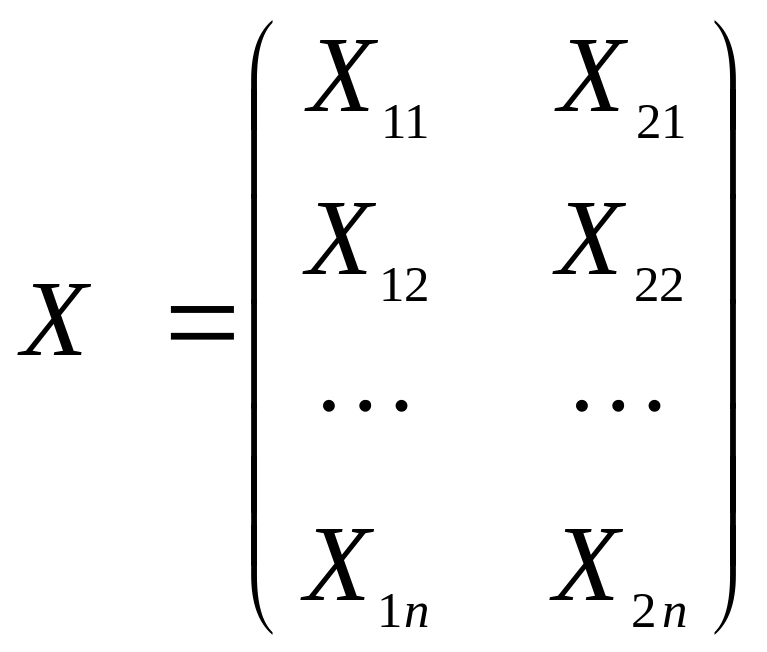
Матрицы и совпадают. Для оценок параметров в соотношении (19) воспользуемся формулой (16)

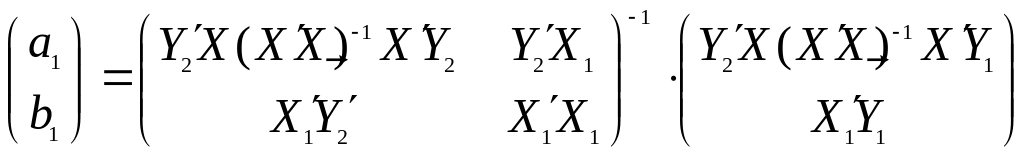(20)

По данным таблицы приведем результаты промежуточных вычислений:

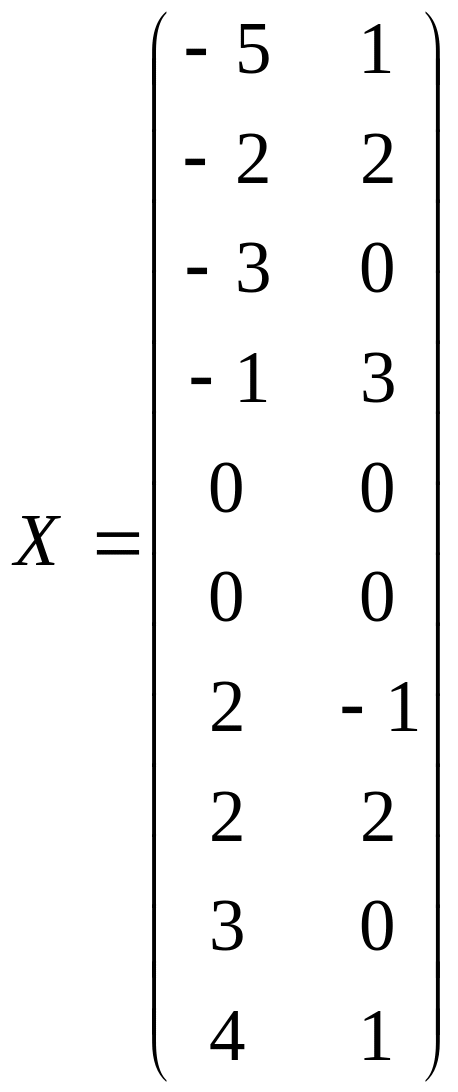
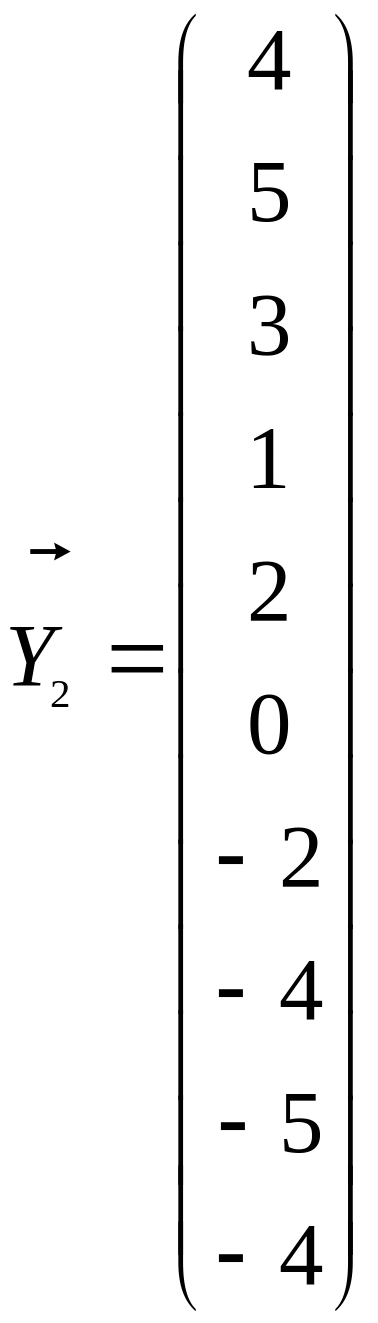
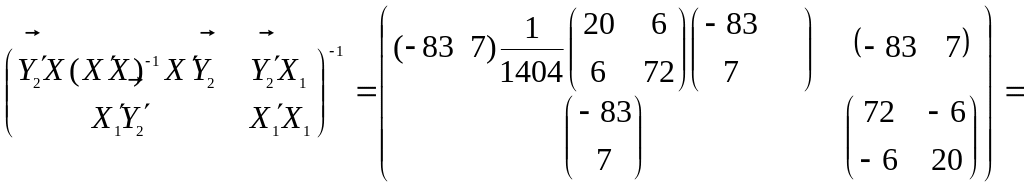
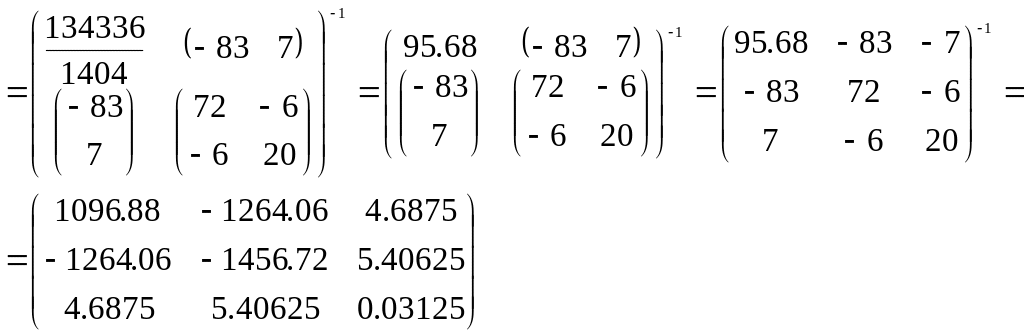
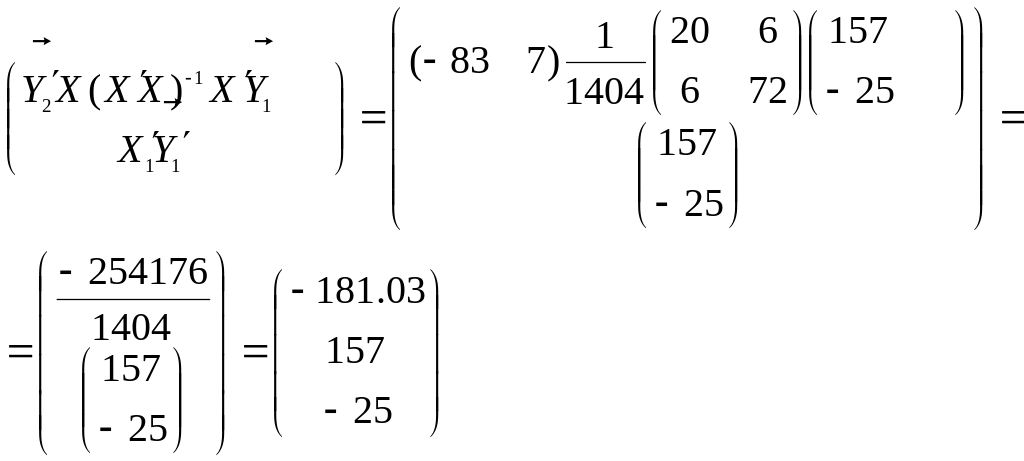
Подставим в (20),эти промежуточные результаты, найдем численные значения искомых параметров:

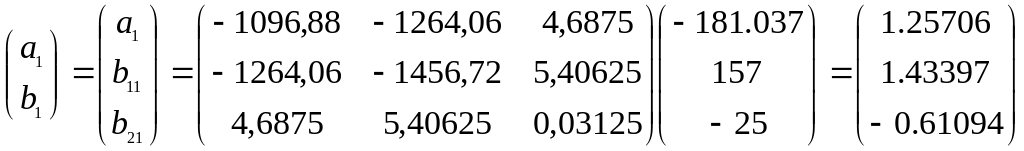
Таким образом, оценка первого уравнения (18) по двухшаговому методу наименьших квадратов имеет вид:

Аналогичным способом можно оценить второе уравнение модели (18). По простому методу наименьших квадратов уравнение регрессии будет иметь вид:

Заметное расхождение отмечается лишь в коэффициенте при переменной .