Тема: ознакомление с составной задачей и формирование умений решать составные задачи
1.Составная задача включает в себя ряд простых задач, связанных между собой так, что искомые одних простых задач служат данными других. Решение составной задачи сводится к расчленению ее на ряд простых задач и последовательному их решению. Таким образом, для решения составной задачи надо установить ряд связей между данными и искомым, в соответствии с которыми выбрать, а затем выполнить арифметические действия.
Рассмотрим в качестве примера задачу: «В школе дежурили 8 девочек, а мальчиков на 2 больше. Сколько детей дежурило в школе?»
Эта задача включает две простые:
1) В школе дежурили 8 девочек, а мальчиков на 2 больше. Сколько мальчиков дежурило в школе?
2) В школе дежурили 8 девочек и 10 мальчиков. Сколько всего детей дежурило в школе?
Как видим, число, которое было искомым в первой задаче (число мальчиков), стало данным во второй (10 мальчиков). Последовательное решение этих задач является решением составной задачи: 1) 8 + 2=10; 2) 8+10=18.
В решении составной задачи появилось новое, здесь устанавливается несколько связей, в соответствии с которыми выбираются арифметические действия. Поэтому проводится специальная работа по ознакомлению и формированию умений решать составные задачи.
2.Ознакомление с составной задачей и формирование умений решать составные задачи
Подготовительная работа к ознакомлению с составными задачами должна помочь учащимся уяснить основное отличие составной задачи от простой —для решения надо вычленить простые задачи, установив соответствующие связи между данными и искомым Упражнения:
1) Решение простых задач с недостающими данными, например:
а) В колхозе были грузовые машины и 4 легковые. Сколькo всего грузовых и легковых машин было в колхозе?
б) На экскурсию поехали мальчики и девочки. Сколько всего детей поехало на экскурсию?
После чтения таких задач учитель спрашивает, можно ли узнать, сколько всего машин было в колхозе , почему нельзя . Далее дети подбирают числа и решают задачу.
Выполняя такие упражнения убеждаются, что не всегда можно сразу ответить на вопрос задачи, так как может не хватать числовых данных, их надо получить (подобрать числа, а при решении составных задач найти, выполнив соответствующее действие).
2) Решение пар простых задач, в которых число, полученное в ответе на вопрос первой задачи, является одним из данных во второй задаче:
а) У Саши было 6 пластинок со сказками и 4 пластинки с детскими песнями. Сколько всего пластинок было у Саши?
б) У Саши было 10 пластинок, он подарил одну пластинку товарищу. Сколько пластинок осталось у Саши?
В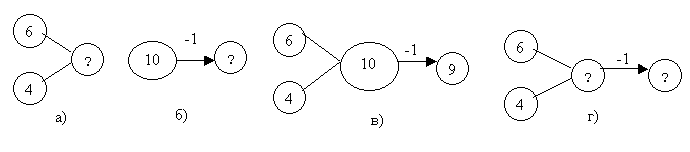
ходе решения этих задач составляют их
модели
После их решения, заметив, что ответ первой задачи является условием второй, модели а) и б) объединяют в схему в), для чего знаки вопроса заменяют полученными ответами. Теперь делаем предположение: "Заменим полученные ответы в схеме в) знаками вопроса и посмотрим, что у нас получится. (Заменив, получим модель г)). Посмотрите, мы получили модель, где у нас два вопроса. Скоро мы с вами будем учиться решать такие задачи". Заметим, что здесь идет процесс конструирования составной задачи.
3) Решение задач с двумя вопросами, где удаление одного вопроса превращает простую задачу в составную. Например, в задаче: "Столяр сделал 8 книжных полок, а кухонных полок на 3 меньше. Сколько кухонных полок сделал столяр? Сколько всего полок сделал столяр?", после решения 1) 8-3=5 (полок), 2) 8+5=13(полок) учитель беседует: "Прочитайте задачу без первого вопроса. (Читают.) Решением новой задачи будет одно или два действия? (Два действия.) Значит, новая задача будет решаться в двух действиях. С такими задачами мы скоро еще встретимся".
Для знакомства с составной задачей специально отводится в I классе два-три урока, на которых особое внимание уделяется установлению связей между данными и искомым, составлению плана решения и записи решения.
Первыми включают задачи, при решении которых надо выполнить два различных арифметических действия: сложение и вычитание. При этом содержание задач должно позволять иллюстрировать их.