6.2. Метод потенциальных функций.

Пусть требуется разделить два непересекающихся образа V₁ и V₂. Это значит, что нужно найти функцию положительную в точках образа V₁ и отрицательную в точках образа V₂.

В процессе обучения с каждой точкой обучающей последовательности связывается потенциальная функция (по аналогии с потенциалом электрического поля вокруг точечного электрического заряда, который убывает при удалении от заряда). Если поле образовано несколькими зарядами, то потенциал в каждой точке этого поля равен сумме потенциалов зарядов. Если заряды расположены компактной группой, то потенциал будет максимальным внутри группы. Тогда могут быть построены потенциальные функции для каждого образа:

, .

В качестве разделяющей функции можно выбрать функцию вида

.

Примеры потенциальных функций:

;

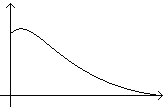
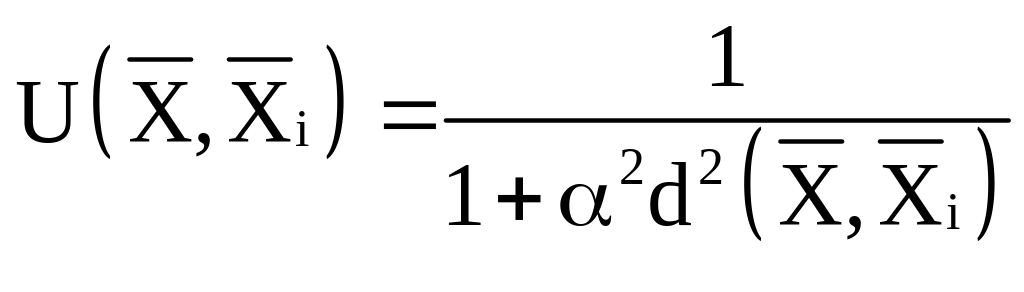
где α – параметр функции;

– расстояние между объектами.

В процессе обучения предъявляется обучающая последовательность и на каждом n-м такте обучения строится приближение по следующей процедуре:

;

где  – положительная константа.

Процесс обучения останавливается, когда перестает меняться.

6.3. Метод предельных упрощений.

Метод использует подход, при котором, в отличие от построения сложных разделяющих поверхностей в заданных пространствах признаков, формируется такое пространство, в котором процесс распознавания очень прост.

В методе предельных упрощений предполагается, что разделяющая функция задается заранее в виде линейного полинома, а процесс обучения состоит в конструировании такого пространства минимальной размерности, в котором эта функция правильно разделяет обучающую последовательность. Алгоритм построения такого пространства предполагает последовательный отбор тех свойств объектов, которые позволяют правильно решить большинство обучающих примеров. Такой отбор признаков продолжается до тех пор, пока не наступит безошибочное линейное разделение образов на обучающей последовательности.

Для разделения образов выбирается гиперплоскость, описываемая уравнением

или 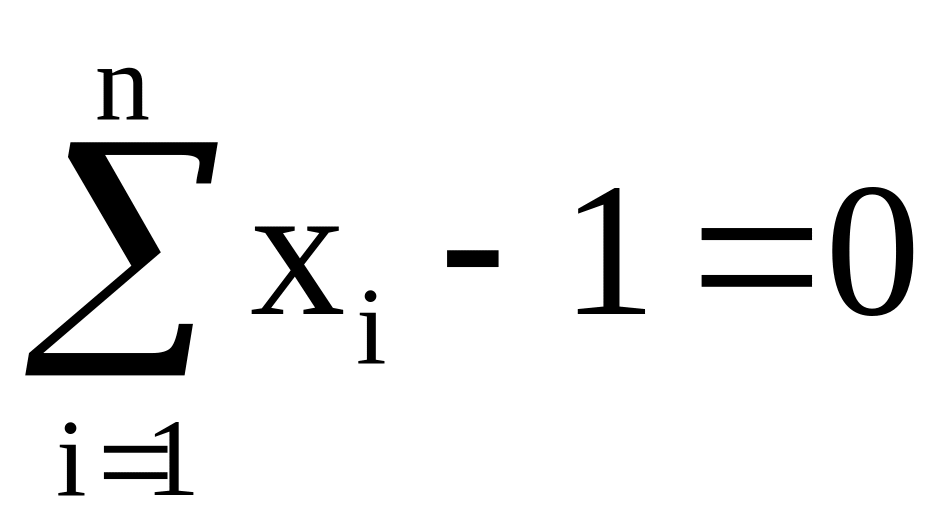, где x_i – i-й признак.

6.4. Коллективы решающих правил.

Этот подход объединяет различные алгоритмы для решения задач распознавания.

Пусть в некоторой ситуации Х принимается решение S. Тогда S = R(X), где R – алгоритм принятия решения в ситуации X. Пусть существует L различных алгоритмов решения задачи, т. е. S_l = R_l(X), где l = 1, ..., L; S_l – решение, получен­ное алгоритмом R_l.

Множество алгоритмов {R} = {R₁, R₂, ..., R_L} называется коллективом алгоритмов решения задачи (кол­лективом решающих правил), если на множестве решений S_l в любой ситуации Х определено решающее правило F, т. е. S = F(S₁, S₂, ..., S_L, X). Алгоритмы R_l называются членами коллектива, S_l – решение l-го члена коллектива, а S – коллек­тивное решение. Функция F определяет способ обобщения ин­дивидуальных решений для получения решения коллектива S.

Выбор правила осуществляется взвешиваньем его компетент­ности в решаемой задаче. Например, вес решающего правила R_l может определяться соотно­шением

где B_l – область компетентности решающего правила R_l.

Веса решающих правил выбираются так, что для всех возможных значений X.

Такой подход представляет собой двухуров­невую процедуру распознавания: на первом уровне определяется принадлежность образа той или иной области компетент­ности, а на втором – вступает в силу решающее правило, компетентность которого максимальна в найденной области.