2.3 Якісний розгляд вільних коливань в дисипативних системах
Звернемося до подання розглянутого руху на фазовій площині. Відома процедура методу ізоклин призводить до їх рівнянь
(2.6)
де
,
.
Перепишемо рівняння ізоклин (2.6) у вигляді
(2.7)
Нульова ізоклина
тепер
не збігається з віссю
і проходить через другий і четвертий
квандранти (рис.
2.5), коли
(дисипація
позитивна). Фазові траєкторії представляють
спіралі,
що
накручуються на початок координат.
Особлива точка називається стійким
фокусом.
У випадку
(режим
апериодичного
руху) фазовий портрет представляється
деформованими параболами (рис.
2.6), а
особлива точка називається стійким
вузлом.
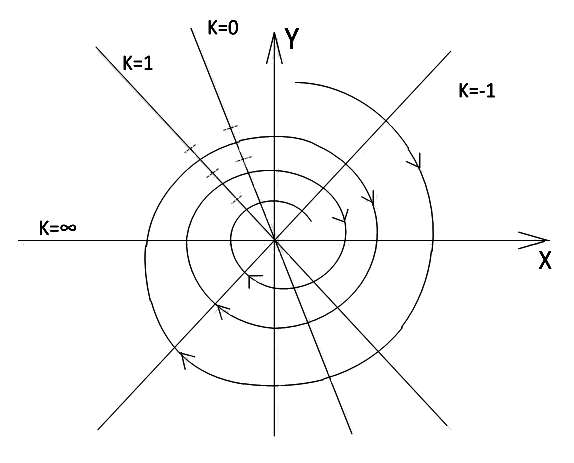
Рисунок 2.5 – Фазовий портрет лінійної системи зі слабкою дисипацією
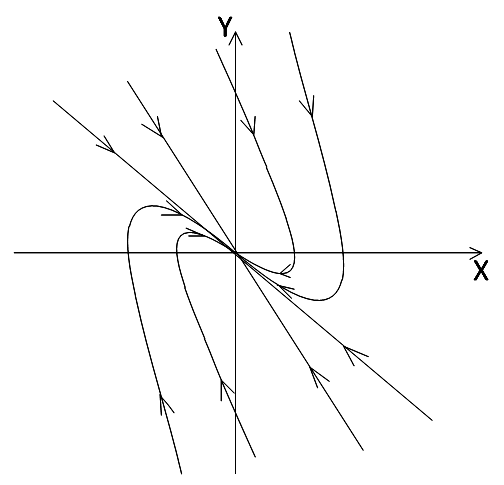
Рисунок 2.6 – Фазовий портрет лінійної системи з сильним загасанням
2.4 Негативна дисипація
Розглянуті вище сили тертя були спрямовані протилежно відповідним швидкостями, сприяли загасанням рухів і називалися дисипативними силами.
Формально можна
припустити існування сил,
які лінійно
залежать від швидкості, але збігаються
з нею за напрямком. У рівнянні (2.1) стане
і його розв’язок
прийме вигляд
тобто коливання будуть наростаючими за будь-яких як завгодно малих початкових збуреннях; положення рівноваги нестійке. Таким чином, такі сили сприяють розгойдуванню коливань. Фазові портрети представлені на рисунках 2.7 і 2.8 з особливими точками - нестійкий фокус і нестійкий вузол відповідно.
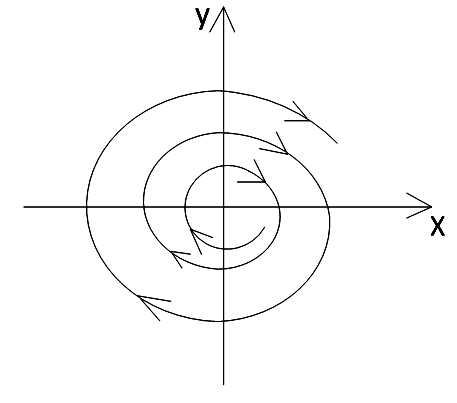
Рисунок 2.7– Фазовий портрет нестійкої рівноваги системи при малому терті
Рисунок 2.8 – Фазовий портрет нестійкої рівноваги при великому терті
Наведемо приклад механічної системи, в якій може виникнути сила «негативного тертя». Обертається з постійною швидкістю барабан 3 (рис. 2.9), щільно притиснутий до тіла 1, закріпленого на пружинах 2.
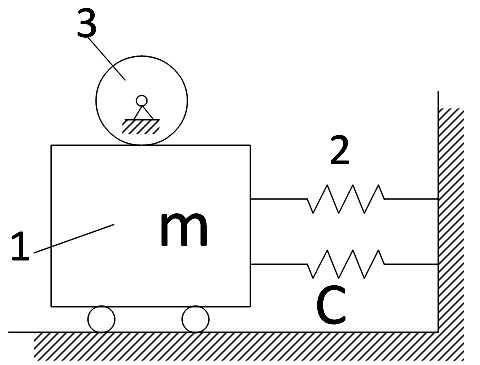
Рисунок 2.9 – Механічна система з негативним тертям
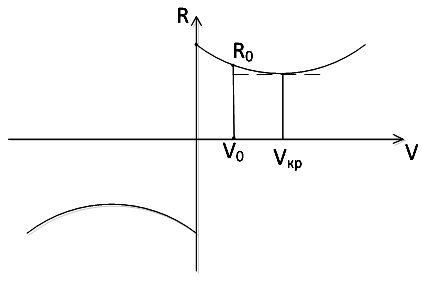
Рисунок 2.10 – Графік залежності сили тертя від швидкості руху
Видима
реальна характеристика сили сухого
тертя між тілами 1 і 3 показана на рис
2.10, де
–
швидкість ковзання при спокої тіла 1.
Диференціальне рівняння руху тіла 1 має вигляд
(2.8)
тут
Враховуючи зміну
при
бачимо, що рівняння (2.8) відповідає
випадку розгойдування коливань.
Зазначимо, що даний розв’язок застосовується лише до пояснення початкової стадії розвитку коливань, тому при зростанні амплітуди слід враховувати нелінійність сил тертя.
Контрольні запитання і завдання до розділу 2
1. Що називають ізоклинами? Наведіть приклади їх використання.
2. Які зміни зазнає фазовий портрет лінійних коливальних систем в разі сильної дисипації?
3. Отримати диференціальне рівняння (2.8) системи з негативним тертям.
4.
Побудувати
фазові портрети для рівнянь:
.
3 Вимушені коливання систем з одним ступенем свободи
Коливальні процеси в системах, що викликаються зовнішнім впливом, що залежить явно від часу і не залежить від руху системи, називають вимушеними коливаннями.
При вивченні зовнішнього впливу розрізняють силовий і параметричний вплив. У першому випадку параметри коливальної системи не змінюються і, навпаки, у другому - змінюються лише параметри.
На рисунках показані прості механічні системи та електрична система при зовнішніх впливах (рис. 3.1 - маятник з силовим впливом, рис. 3.2 - маятник з кінематичним впливом, рис. 3.3 - електричний контур зі збудливою е.р.с.).
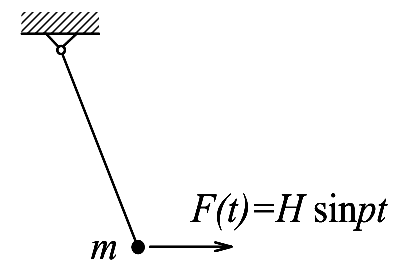
Рисунок 3.1 – Маятник під дією зовнішньої сили
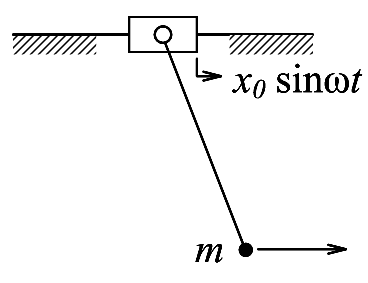
Рисунок 3.2 – Кінематичний вплив на маятник
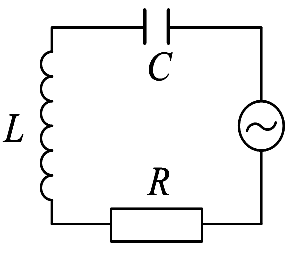
Рисунок 3.3 – Коливальний контур під дією зовнішньої напруги