9.2 Загальні відомості плоского електромагнітного поля

Нехай , , , залежать від і . Розкладемо вектори і на три перпендикулярних вектора, колінеарних осям координат. Для і маємо:

(9.5)

, (9.6)

де кожна складова і дорівнює відповідно складової , помноженої на скаляр або .

Обмежимося випадком ідеального діелектрика і притому незарядженого ( ).Рівняння (9.1) - (9.4) легко спрощуються.

У якості «допоміжної поверхні» візьмемо поверхню паралелепіпеда висоти з квадратною основою, сторони якого паралельні осям і і мають однакову довжину, рівну одиниці.

Застосування до нашої допоміжної поверхні рівнянь (9.1) - (9.4) приводить до наступної системи рівнянь:

, (9.7)

, (9.8)

, (9.9)

, (9.10)

, (9.11)

, (9.12)

, (9.13)

, (9.14)

Рівняння (9.11), (9.14) і (9.12), (9.13) показують, що величини і залишаються постійними. Крім того рівняння (9.7) - (9.14) не встановлюють ніякого зв'язку між собою, а також з усіма іншими компонентами полів і .

Це фізично означає наступне: плоске електромагнітне поле, яке залежить від , є суперпозицією однорідного електростатичного поля, паралельного осі і незалежного від нього однорідного статичного магнітного поля, також паралельного осі і незалежного від цих двох полів електромагнітного поля, вектори , , , якого мають тільки і компоненти (тобто перпендикулярні осі ).

Нас будуть цікавити тільки електромагнітні поля, що поширюються. Враховуючи вищесказане, приходимо до важливого результату: розповсюджуване плоске поле є поперечним полем, в ньому вектори , , , лежать у площинах, перпендикулярних до напрямку поширення.

9.3 Плоскі хвилі

Зауважимо, що розповсюджуване плоске поле є суперпозицією двох не пов'язаних між собою полів:

а) поля, в якому вектори , колінеарні осі , а вектори , осі [рівняння (9.7), (9.10)].

Так як , то (9.7), (9.10) можуть бути замінені наступними:

, . (9.15)

б) поля, в якому, колінеарні осі , а вектори , осі . Аналогічно з (9.8), (9.9) одержимо

, . (9.16)

Поле, що описується рівняннями (9.15), назвемо -полем (по тому, як спрямований в ньому вектор ), а поле (9.16) -полем.

Кожне з цих полів не є ні чисто електричним, ні чисто магнітним, обидва є електромагнітними полями.

Розглянемо спочатку -поле. З рівнянь (9.15) легко отримати

. (9.17)

Це хвильове рівняння. Електрична компонента - хвилі поширюється у вигляді хвилі, що деформується, зі швидкістю:

Тут же отримуємо для компоненти рівняння

(9.18)

тобто магнітна складова поширюється з тією ж швидкістю, що і електрична компонента.

Таким чином, замість «- поля» можна говорити « - хвиля».

Використовуючи розв’язок хвильових рівнянь (9.17), (9.18) у вигляді гармонійних функцій можна знайти, що

. (9.19)

Тобто в кожній точці і в кожний момент часу магнітна компонента пропорційна електричній компоненті.

Для - хвилі аналогічно виходить:

.

Як в - хвилі так і в - хвилі вектори , перпендикулярні один до одного і до напрямку поширення (див. рис. 9.1).

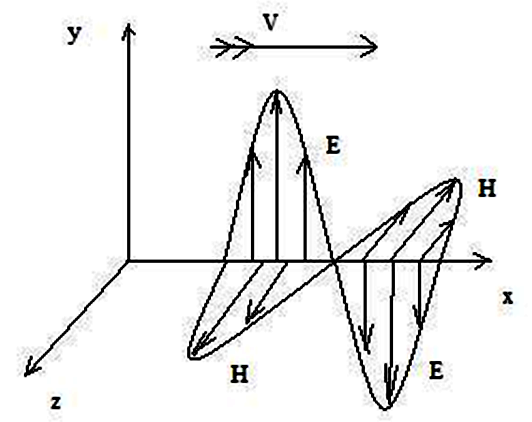
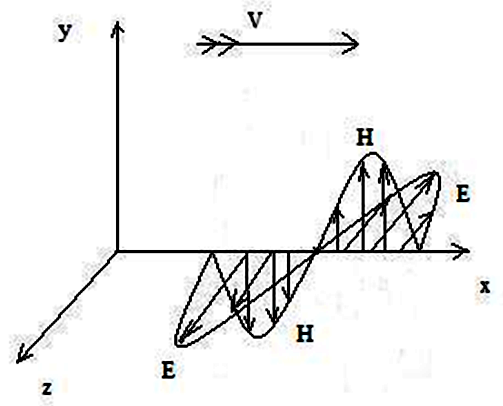
Рисунок 9.1 – Уявлення про структуру поля в електромагнітної y- і z-хвилях