7. Анализ чувствительности скорректированной системы.

Для проведения анализа чувствительности скорректированной системы приведем таблицу (см. табл. 1.) с такими параметрами, как - коэффициент усиления нестабильного звена (УМ),- время регулирования иM– показатель колебательности, и попытаемся скорректировать последние два показателя по критериям, указанным в задании, варьируя.Mдолжно быть меньше 1.3, аминимально из набора всех полученных.

10	1.86	4.45
20	1.02	3.66
40	0.50	2.70
80	0.31	1.72
90	0.19	1.55
100	0.15	1.09
110	0.16	1.25
150	0.21	1.62

Табл.1. Анализ чувствительности скорректированной системы.

Из данной выборки лучшими значениями оказались время регулирования, равное 0.15 сек. и показатель колебательности, равный 1.09 при коэффициенте усиления УМ, равном 100.

8. Анализ нелинейной системы.

С помощью пакета MATLAB/Simulink введем модель системы в ЭВМ. Получим следующую схему:

Рис. 12. Схема откорректированной системы, полученная путем моделирования на MatLab/Simulink.

После моделирования процесса в MATLAB/Simulink видно, что результаты (см. рис. 13) совпадают с результатами, полученными при помощи программы CLASSIC (см. рис. 10).

Рис.13. График переходного процесса откорректированной системы, полученный путем моделирования на MatLab/Simulink.

Введем в систему нелинейный элемент (НЭ):

- люфт с ограничением на выходе двигателя(deadzone).

Получим следующую схему:

Рис. 14. Схема откорректированной системы с НЭ, полученная путем моделирования на MatLab/Simulink.

Изменяя параметры НЭ, определим граничные значения параметров, при которых в системе возникает неустойчивость (см. табл. 2), и приведем графики на выходе НЭ и переходного процесса под его воздействием:

Люфт
±0	0.15	52.86
±10	0.15	45.04
±20	0.15	38.17
±30	0.29	31.23
±40	0.38	24.72
±80	-	4.93

Табл. 2. Анализ устойчивости системы с НЭ.

Анализ таблицы 2 и рисунков 16 – 21 показывает, что система остается устойчивой при любом изменении параметров люфта в диапазоне от ±0 до ±100.

Рис.16. График переходного процесса на выходе звена коррекции с ограничением, полученный путем моделирования на MatLab/Simulink. Граничные параметры люфта равны ±80.

Рис.17. График переходного процесса на выходе системы, полученный путем моделирования на MatLab/Simulink. Процесс устойчивый, граничные параметры люфта равны ±80, перерегулирование равно 4.93.

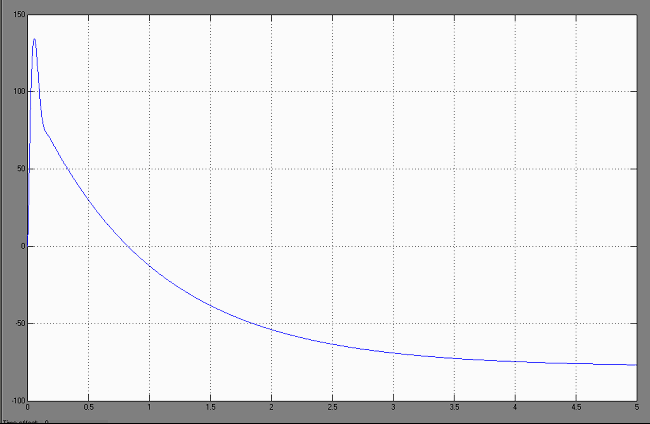
Рис.18. График переходного процесса перед входом в люфт, полученный путем моделирования на MatLab/Simulink. Граничные параметры люфта равны ±80.

Рис.19. График переходного процесса на выходе звена коррекции с ограничением, полученный путем моделирования на MatLab/Simulink. Граничные параметры люфта равны ±40.

Рис.20. График переходного процесса на выходе системы, полученный путем моделирования на MatLab/Simulink. Процесс устойчивый, граничные параметры люфта равны ±40, время регулирования равно 0.38, перерегулирование равно 24.72.

Рис.21. График переходного процесса перед входом в люфт, полученный путем моделирования на MatLab/Simulink. Граничные параметры люфта равны ±40.

Рис.22. График переходного процесса на выходе звена коррекции с ограничением, полученный путем моделирования на MatLab/Simulink. Граничные параметры люфта равны ±0.

Рис.23. График переходного процесса на выходе системы, полученный путем моделирования на MatLab/Simulink. Процесс устойчивый, граничные параметры люфта равны ±0, время регулирования равно 0.15, перерегулирование равно 52.86.

Рис.24. График переходного процесса перед входом в люфт, полученный путем моделирования на MatLab/Simulink. Граничные параметры люфта равны ±0.