Министерство образования РФ.

Санкт-Петербургский государственный электротехнический университет.

Кафедра АиПУ

Отчет.

По лабораторной работе № 2

« Метод гармонического баланса »

Выполнили: Рачеев Р.А.

Смирнов И.А.

Кудряшов В.В.

Факультет: КТИ

Группа: 9322

Проверил: Имаев Д. Х.

Санкт-Петербург

2001

Целью работы является освоение метода приближенного исследования периодических режимов в релейных системах и проверка результатов с помощью компьютерной имитации.

Пример 1.

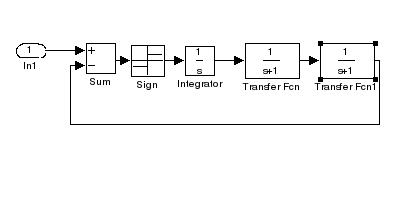
Компьютерной имитацией получаем, что НЭ соответствует следующая гармоническая функция:

Рис. 1.

Где период Т=6,25

  1 с

A = 0.6

Теоретический расчет.

Из теории мы знаем, что коэффициент гармонической линеаризации q(A)

для идеального реле равен

Где с – значение функции при x0 (c=1)

Так как мы имеем систему с однозначной СХ (), то для определения параметров гармонического решения мы можем воспользоваться методикой Е.П. Попова. Запишем ХП замкнутой системы

Для нашей системы он будет выглядеть так:

В соответствии с критерием Гурвица, чтобы система находилась на границе устойчивости, предпоследний определитель должен равняться нулю:

остальные должны быть положительными.

Для нашего случая:

Зная, что с=1 можем найти амплитуду А.

Чтобы найти , надо в ХП подставить вместо s комплексную частоту j, а вместо амплитуды - найденное выше значение . Получим:

=1 рад/c

=6,28 с

Компьютерной имитацией мы получили, очень близкие к теоретическим, результаты, что доказывает уместность примененного метода для данной замкнутой системы.

Пример 2.

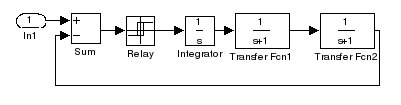
Где блок Relay представляет собой реле с гистерезисом (с=1, b=1).

Компьютерной имитацией получаем, что НЭ соответствует следующая гармоническая функция:

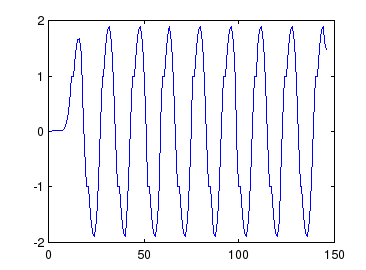
Рис.2.

По графику находим:

А= 1,9

Т=12,5 с

= 0,5024 рад/с

Теоретический расчет.

Реле с гистерезисом имеет неоднозначную СХ. Для реле с гистерезисом коэффициенты гармонической линеаризации равны:

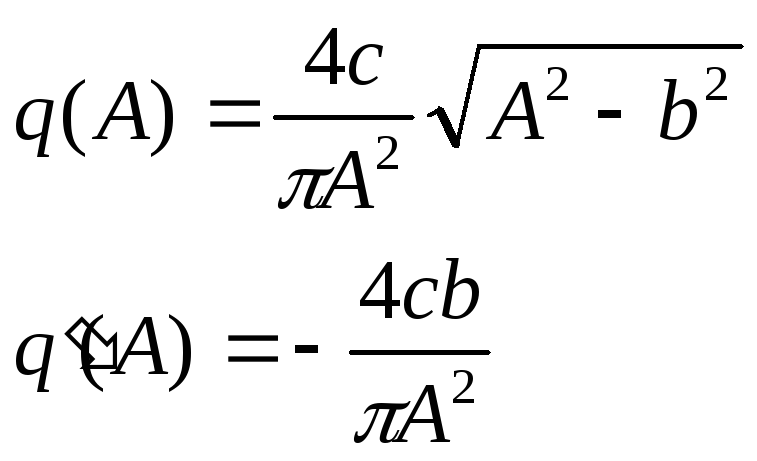
Очевидно, что , следовательно, неприменима методика Е.П. Попова. Для этого случая лучше использовать методику Л.С. Гольдфарба, основанную на критерии Найквиста.

Напомним критерий Найквиста:

Если АФХ разомкнутой системы охватывает критическую точку (-1), то замкнутая система неустойчива. Граница устойчивости достигается при прохождении АФХ точно через критическую точку. Методика Л.С. Гольдфарба звучит так:

Это условие обычно записывают так:

Удобство такого представления – левая часть зависит только от , а правая – от А. Строят две характеристики и их точка пересечения дает искомые параметры  и А.

Построим для нашей системы эти две характеристики:

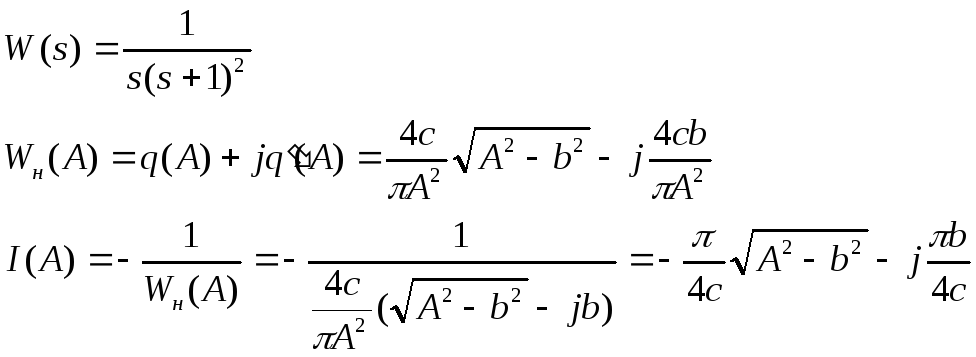
Строим графики W(s) и I(A) и находим, что в точке пересечения = 0,465 рад/с и А=2. Период соответственно равен Т=6,28/0,5=12,56 с. Результаты имитации практически совпадают с теоретической оценкой.

Пример 3.

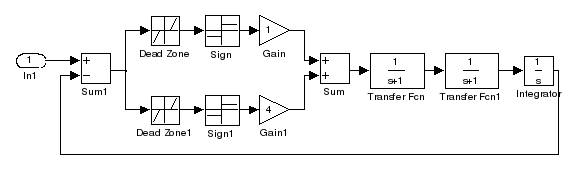
Система представляет собой последовательное соединение нелинейного объекта, график которого представлен на рис.3, и линейной части.

Данный НЭ реализован, как параллельное соединение двух последовательных НЭ, и его коэффициенты гармонической линеаризации (КГЛ) равны сумме КГЛ первого НЭ и второго:

где - КГЛ идеального реле (с1=1), сдвинутого на b1; - КГЛ идеального реле (с2=5), сдвинутого на b2.

Компьютерной имитацией получаем:

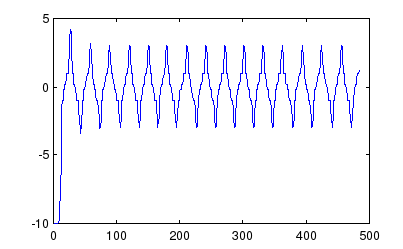
Рис. 4.

А=3

Т=6,67 с

=0,94 рад/с

Фазовый портрет изображен на рис. 5.

Рис. 5.

Легко заметить на ФП два устойчивых замкнутых контура. Это связано с тем, что наш НЭ имеет две зоны нечувствительности. При амплитудах меньших, чем b1, на выходе ничего нет.

ХП замкнутой системы равен:

Автоколебания будут при

График зависимости q(A) представлен на рис.6.