Интервал

Интервалом между событиями или расстоянием между двумя мировыми точками в четырёхмерном пространстве-времени называется величина

.

Пространство, в котором расстояние между двумя точками определяется таким выражением называется псевдоэвклидовым.

В обычном пространстве (эвклидовом)

тогда .

Допустим, что рассматриваются события, происходящие с одной и той же частицей. Тогда – скорость частицы и

.

Поскольку с – константа, а Δτ – инвариант, то и интервал ΔS также оказывается инвариантом.

В общем случае интервал может быть вещественным , мнимым и равным нулю ( , то есть, для светового сигнала).

Вследствие инвариантности интервала

.

Пусть в К^*-системе (события пространственно совмещённые). Тогда для вещественного интервала , т.е. события не могут быть одновременными. Поэтому вещественные интервалы называют времениподобными.

Мнимые интервалы называют пространственноподобными.

Преобразование скоростей

Для К^*-системы , движущейся относительно К-системы с постоянной скоростью υ₀ вдоль оси ОХ получаем из преобразований Лоренца для координат и времени:

.

Так как

,

то

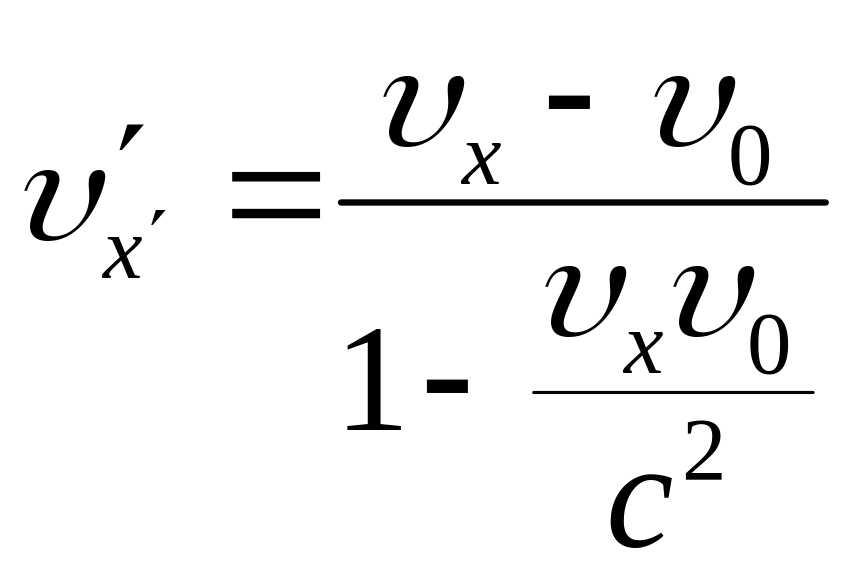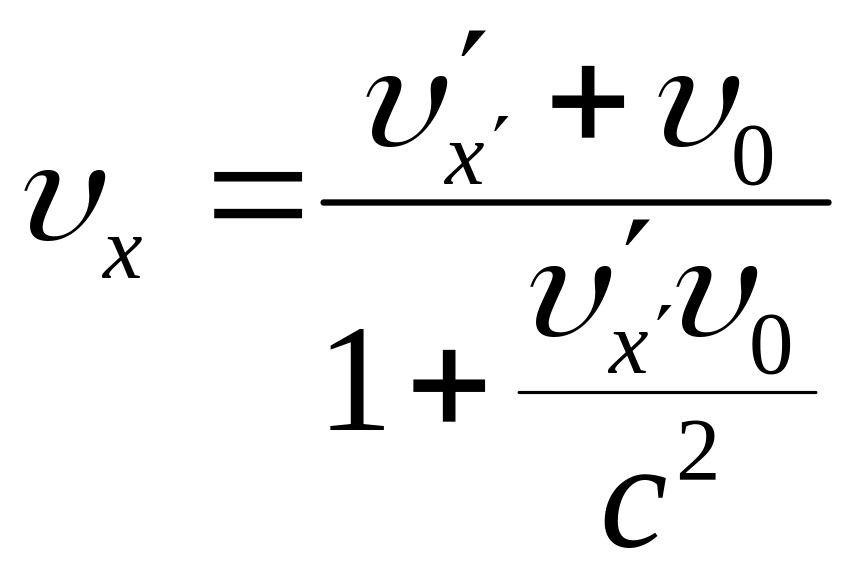
и

и

и

Эти формулы выражают закон сложения (преобразования) скоростей в релятивистской кинематике.

В пределе при (при этом ) они приводят к классическому закону сложения скоростей в классической механике Ньютона:

; ; и .

Как бы ни были близки к с скорости двух частиц, их относительная скорость друг относительно друга всегда меньше с .

Пример: две частицы движутся вдоль оси ОХ К-системы (лабораторной системы отсчёта) навстречу друг другу со скоростями υ₁ = 0,9с и υ₂ =0,7с .

Будем считать, что частица 2 неподвижна в К^*-системе, т.е. . Тогда υ₁ = υ_{х ,} а относительная скорость

Получаем:

Элементы релятивистской динамики

Из принципа относительности следует, что математическая запись любого закона физики должна быть одинаковой во всех инерциальных системах отсчёта. Это означает, что уравнения, описывающие какое-либо явление в К^*-системе, получаются из уравнений, описывающих то же самое явление в К-системе путём простой замены всех нештрихованных величин на штрихованные (условие ковариантности или условие лоренц-инвариантности).

Релятивистским импульсом материальной точки называют величину

.

Величину называют релятивистской массой, а т – массой частицы (иногда называют массой покоя), одинаковой во всех системах отсчёта (инвариантной).

Опыт подтверждает, что приведённый выше релятивистский импульс частицы действительно подчиняется закону сохранения независимо от выбора инерциальной системы отсчёта.

Основное уравнение динамики в релятивистской динамике принимает вид .

Видно, что сила F зависит от скорости . Т.е. в разных системах отсчёта её числовое значение и направление будут различны (неинвариантны).