Преобразования Лоренца

.

Подобно тому как классические представления о пространстве и времени формулируются количественно с помощью преобразований Галилея для координат и времени, новые релятивистские представления о пространстве и времени формулируются с помощью преобразований Лоренца.

П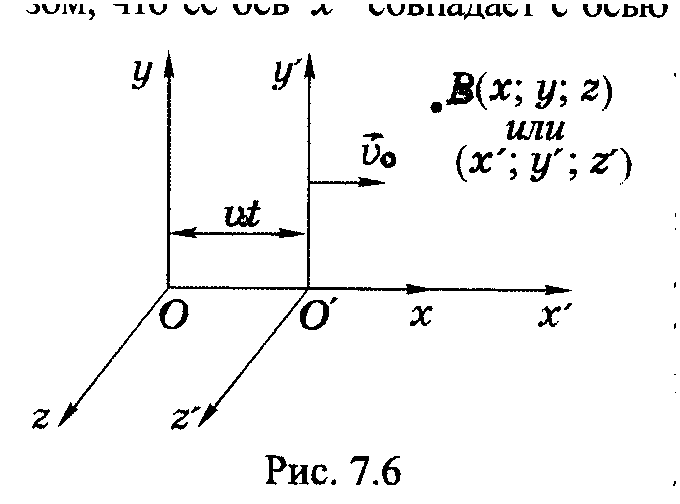 усть имеется инерциальная система отсчёта К . координаты любой точки, например, точки В , в этой системе обозначим через х, у, z , а время через t. Другая инерциальная система К^* движется с постоянной скоростью относительно системы К , а оси y^* и z^* параллельны соответствующим осям y и z (это означает рассмотрение частных преобразований, а не общих). Начало отсчёта времени выбраны таким образом, чтобы в момент времени t = 0 точки О и О^* совпадали.

и

в К-системе

в К^*-системе . Следовательно

, где

– некоторая константа.

Аналогично: в К^*-системе

в К-системе и

.

Из равноправия систем К и К^* вытекает, что коэффициент пропорциональности в обоих случаях должен быть один и тот же.

Для произвольной точки В получаем

Для нахождения коэффициента используем 2-ой постулат СТО. Пусть в момент времени t = t^* = 0 в направлении осей х и х^* посылается световой сигнал, который производит вспышку на экране в точке В. Это событие описывается координатой х и моментом t в системе К и координатой х^* и моментом t^* в системе К^*, причём

и , тогда

Перемножив два последних уравнения, получаем

или .

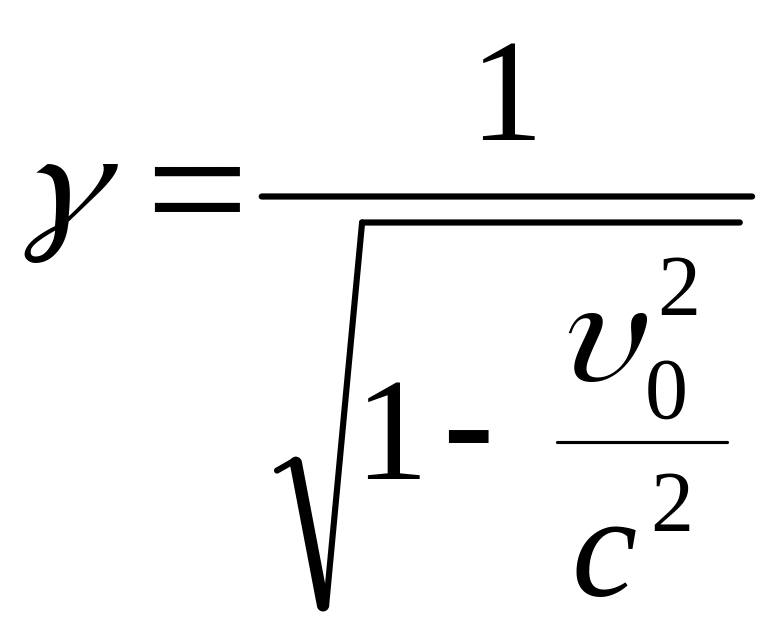Для координат получаем

и , где

.

Для получения формулы, определяющей t по известным t^* и х^* исключаем координату х из исходной системы уравнений

или

Так же получают

.

Зависимости ; ; и называют преобразованиями Лоренца.

В пределе, при и при β << 1 преобразования Лоренца практически не отличаются от преобразований Галилея.

Различие в течение времени в разных системах отсчёта обусловлено существованием предельной скорости распространения взаимодействий.

При выражения для становятся мнимыми. В этом проявляется то обстоятельство, что движение со скоростями, большими с невозможно.

Для запоминания удобна следующая запись

.

Кинематические следствия из преобразований Лоренца

1). Одновременность событий в разных системах отсчёта

Пусть в системе К в точках х₁ и х₂ происходят одновременно два события в момент времени t₁ = t₂ = τ. Тогда в системе К^* этим событиям будут соответствовать моменты

и т.е.

если в К-системе события пространственно разобщены, то в К^*-системе они не будут одновременными .

Это означает, что в одних системах событие 1 будет предшествовать событию 2, а в других системах может быть наоборот. Сказанное относится лишь к событиям, между которыми отсутствует причинная связь. (Рождение элементарной частицы во всех системах отсчёта происходит раньше её распада и ни в одной из систем ребёнок не рождается раньше его родителей).