Лекция 6 Свободные затухающие колебания

Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системы.

Свободные колебания реальных систем всегда затухают. Затухания свободных механических колебаний вызываются главным образом трением, сопротивлением окружающей среды и возбуждением в ней упругих волн.

Система называется линейной если параметры, характеризующие существенные в рассматриваемом процессе физические свойства системы, не изменяются в ходе процесса. Линейные системы описываются линейными дифференциальными уравнениями.

Пример: свободные затухающие колебания пружинного маятника массы т , движущегося в вязкой среде вдоль оси ОХ. На маятник действуют две силы: сила упругости пружины F_упр и сила сопротивления среды F_c , которую, как показывает опыт, можно считать часто прямо пропорциональной скорости υ и направленной в противоположную скорости сторону:

, где

r – постоянный положительный коэффициент пропорциональности, называемый коэффициентом сопротивления.

По второму закону Ньютона по оси ОХ

или

, где .

В любом физическом процессе, который можно описать с помощью дифференциального уравнения типа

– коэффициент затухания;

ω₀ – циклическая частота свободных незатухающих колебаний той же системы, т.е. в отсутствии потерь энергии (β = 0).

В курсе математического анализа доказывается, что решение этого дифференциального уравнения следует искать в форме , а его общее решение .

С₁ и С₂ – постоянные коэффициенты, зависящие от начальных условий;

δ₁ и δ₂ – корни характеристического уравнения .

Если , то корни характеристического уравнения комплексно-сопряжённые:

, где

– мнимая единица.

Общее решение дифференциального уравнения затухающих колебаний имеет вид

.

Используя формулу Эйлера для комплексных чисел

получаем

.

Вводя вместо С₁ и С₂ новые две постоянные А₀ и ψ₀ , связанные с С₁ и С₂ соотношениями

получаем окончательно

.

Значения А₀ и ψ₀ определяют из начальных условий, т.е. из значений S и в начальный момент времени (t =0).

График зависимости S(t) при затухающих колебаниях имеет вид

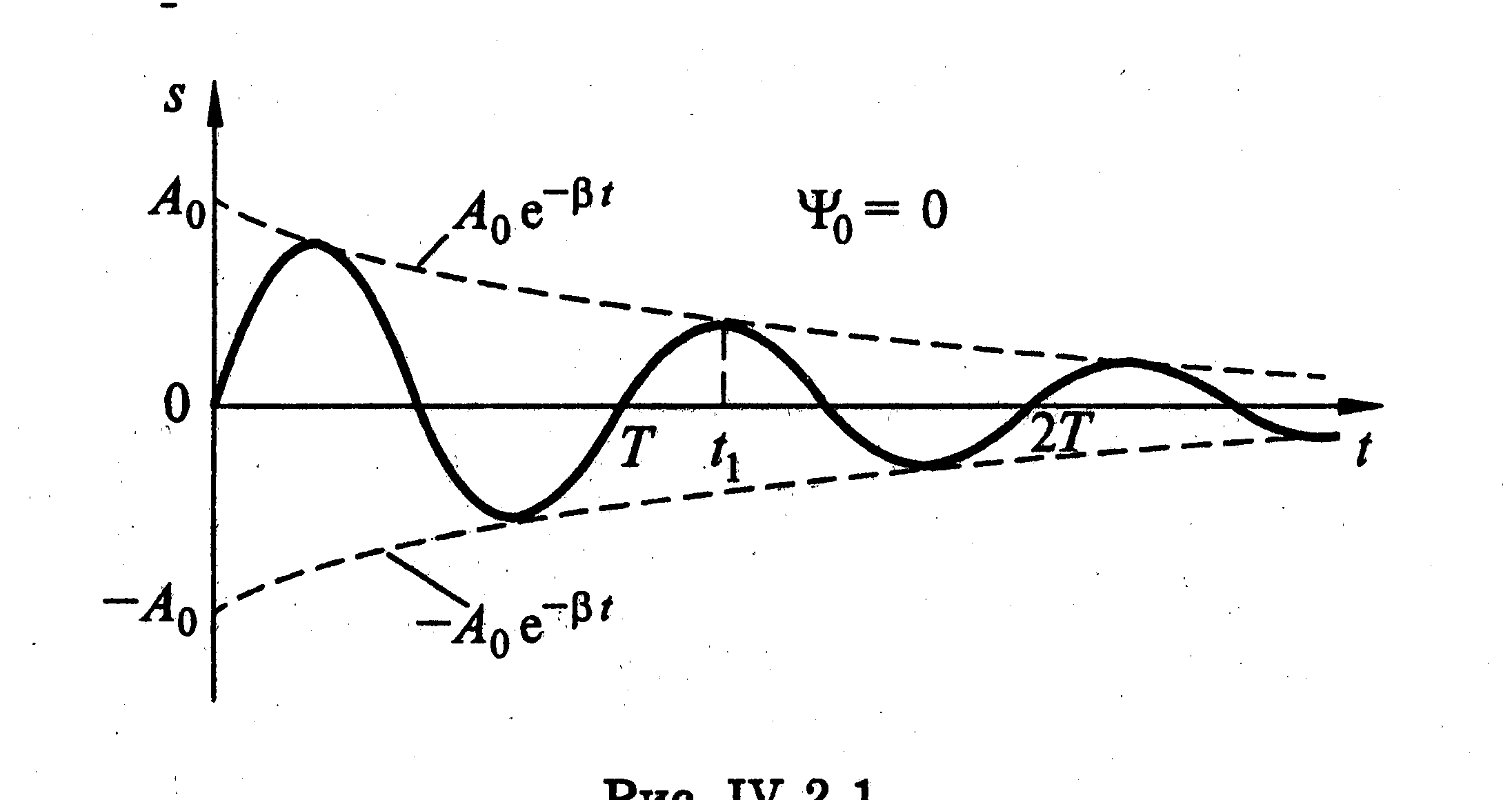
Затухающие колебания не являются периодическими, так как амплитуда колебаний всё время уменьшается, но величину обычно называют условным периодом, а ω – условной циклической частотой затухающих колебаний.

– амплитуда затухающих колебаний;

А₀ – начальная амплитуда.

– время релаксации, т.е. время, в течение которого амплитуда колебаний уменьшается в е раз.

Для количественной характеристики быстрого убывания амплитуды затухающих колебаний пользуются понятием логарифмического декремента – λ

, где

N_e – число колебаний, в течение которых амплитуда уменьшается в е раз.

Так как и , то

и .

Энергия затухающих колебаний складывается из потенциальной и кинетической . После подстановке сюда и получаем зависимость E(t), которая графически представлена на рисунке

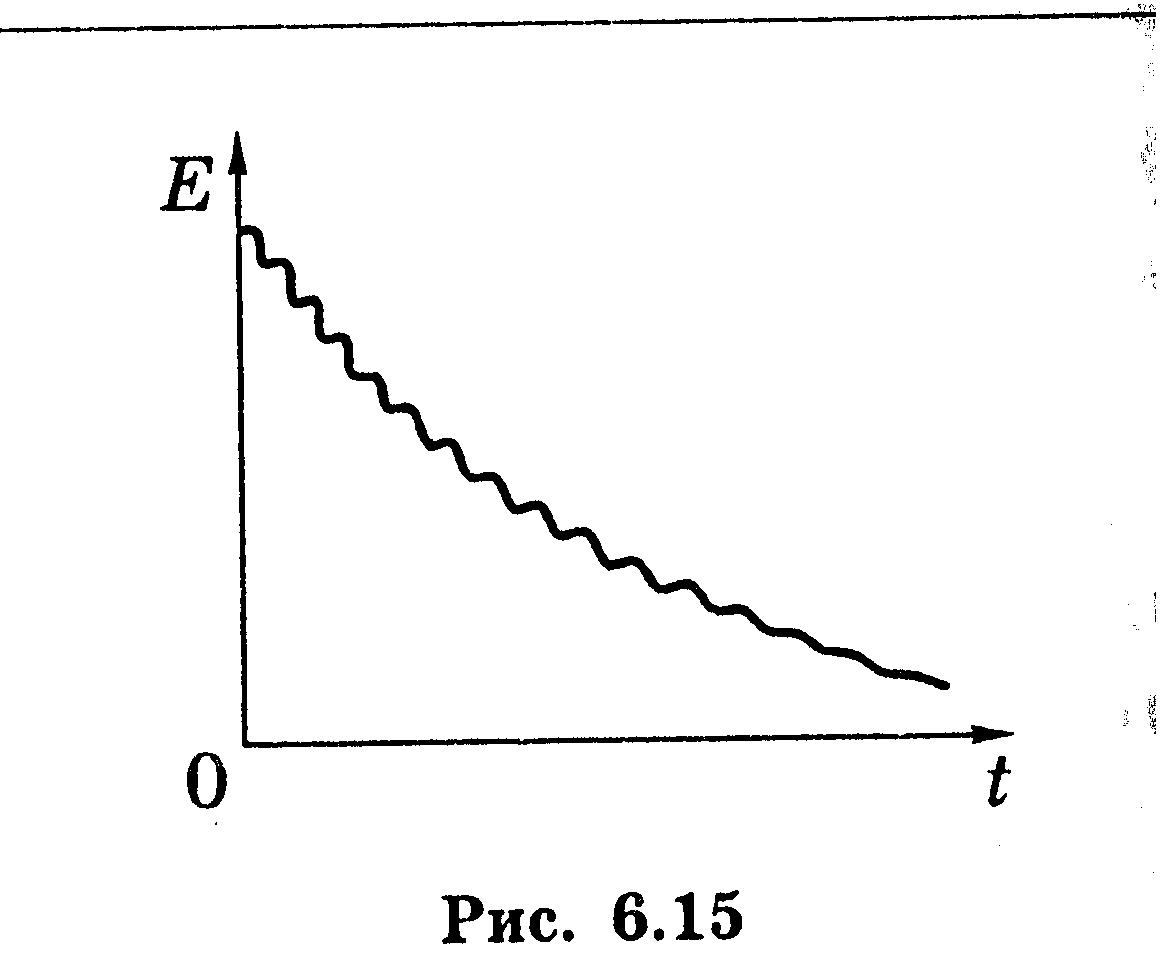
Уменьшение энергии колебаний обусловлено работой силы сопротивления. Мощность этой силы равна

.

Таким образом, кроме тех моментов, когда υ = 0.

При малом затухании (β << ω₀) зависимость E(t) становится практически эквипотенциальной: и убыль энергии в этом случае

.

Добротностью колебательной системы называется безразмерная величина Q , равная произведению 2π на отношение энергии колебаний системы в произвольный момент времени t к убыли этой энергии за промежуток времени равный одному условному периоду затухающих колебаний (от t до t + Т)

.

Так как E(t) пропорциональна A²(t) то

При малых значениях логарифмического декремента (λ << 1) можно принять и для этого случая

Для гармонического осциллятора (пружинного маятника) при малом затухании получаем

.

При достаточно большом затухании система совершает апериодическое движение. Выведенная из положения равновесия, она возвращается в это положение.

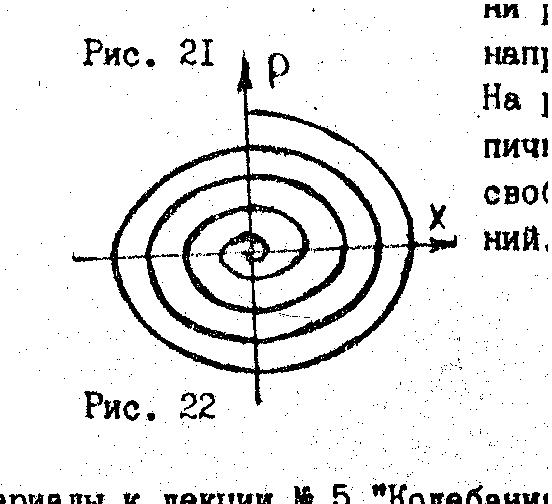
Фазовая траектория свободных затухающих колебаний имеет форму спирали