
Модуль 3.
ЗАНЯТИЯ 9, 10. Подпространства векторного пространства.
Доказать, что множество
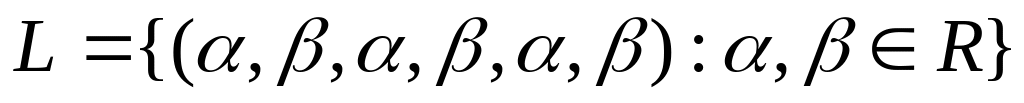 является подпространством векторного
пространства
является подпространством векторного
пространства
 .
Найти его размерность и базис.
.
Найти его размерность и базис.Найти размерность r и базис B линейной оболочки векторов:
 .
Ответ: r=3,
.
Ответ: r=3,
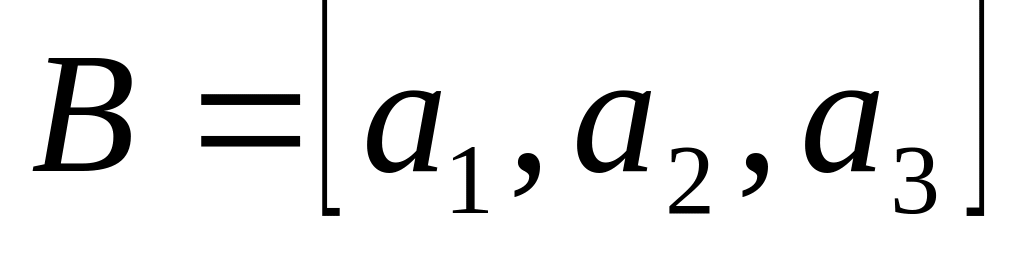 и
и
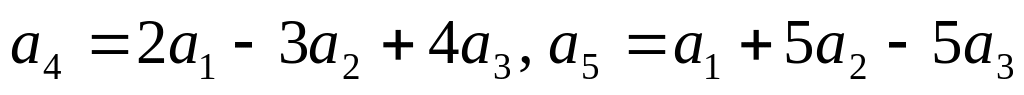 .
.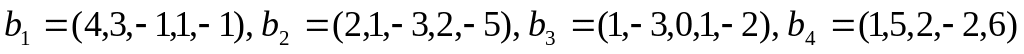 .
Ответ: r=3,
.
Ответ: r=3,
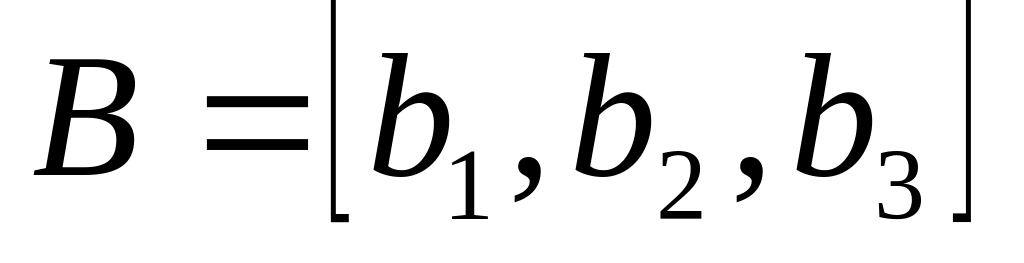 и
и
 .
.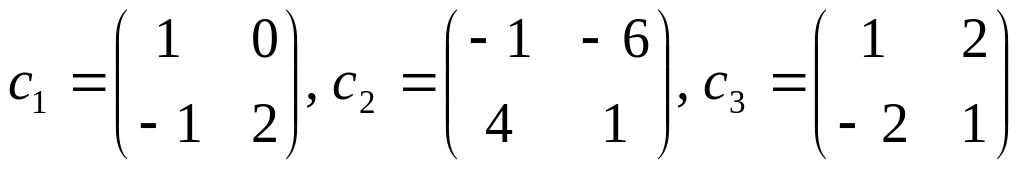 .Ответ:
r=2,
.Ответ:
r=2,
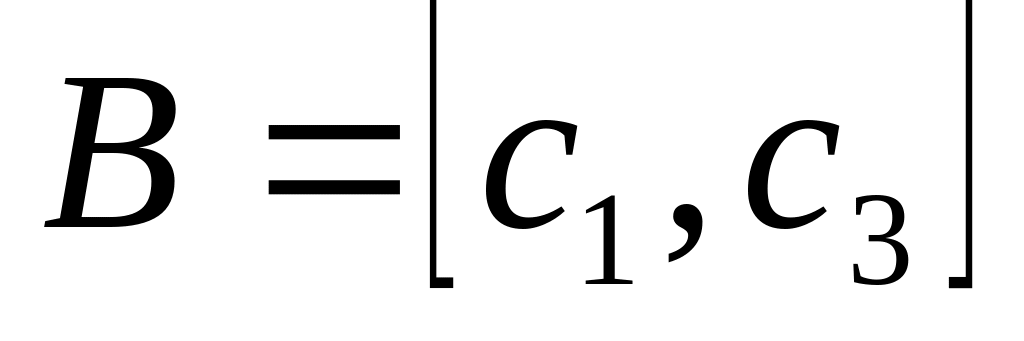 и
и
 .
.
Задать линейную оболочку векторов
 однородной системой линейных уравнений.
Ответ:
однородной системой линейных уравнений.
Ответ:
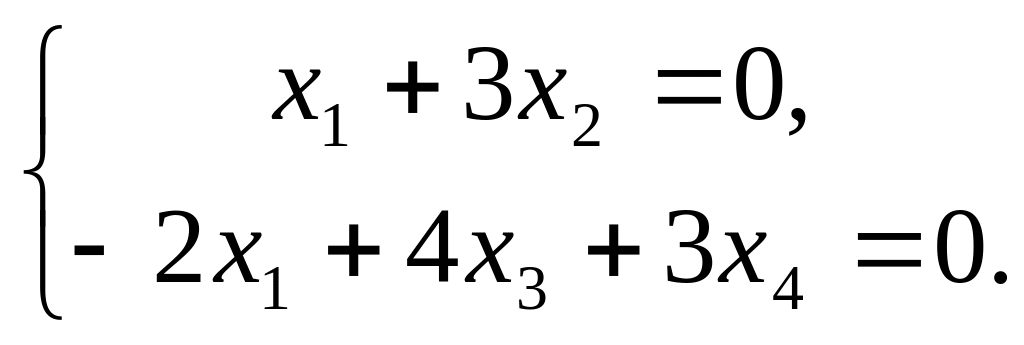
Найти фундаментальную систему решений однородной системы линейных уравнений:
 Ответ:
Ответ:
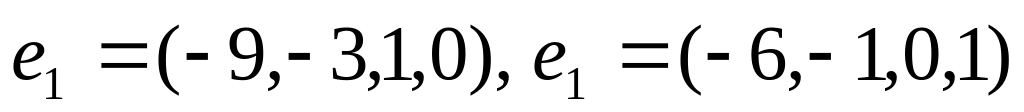 .
.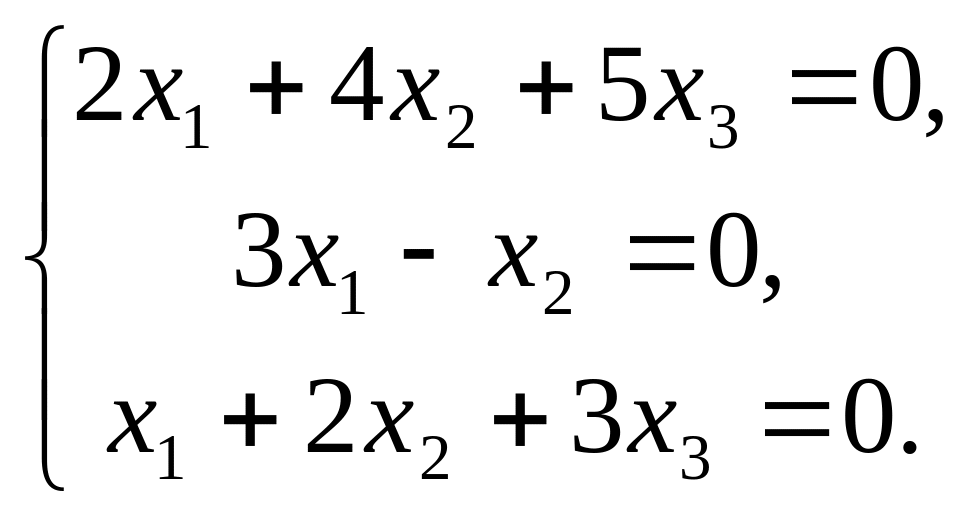 Ответ: система имеет только нулевое
решение.
Ответ: система имеет только нулевое
решение.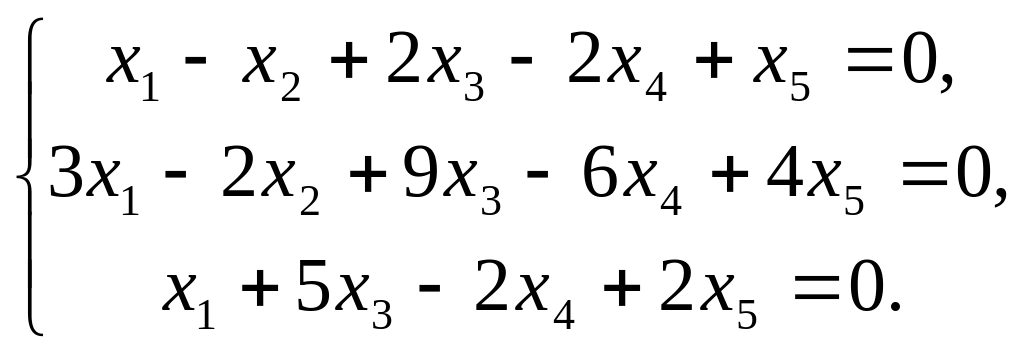 Ответ:
Ответ:

Найти базисы и размерности для суммы и пересечения подпространств
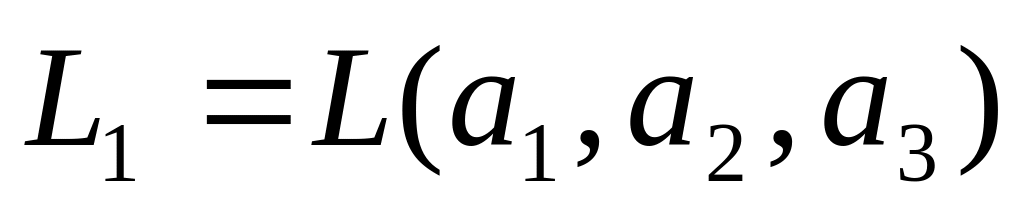 и
и
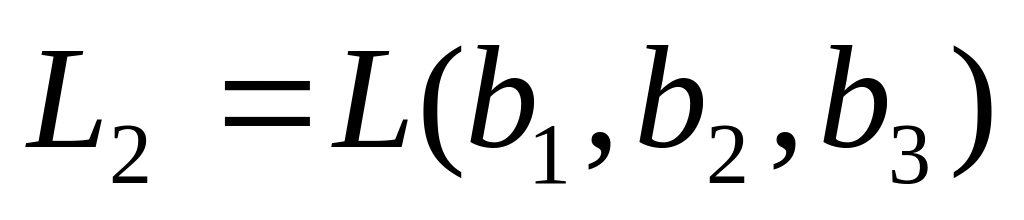 пространства
пространства
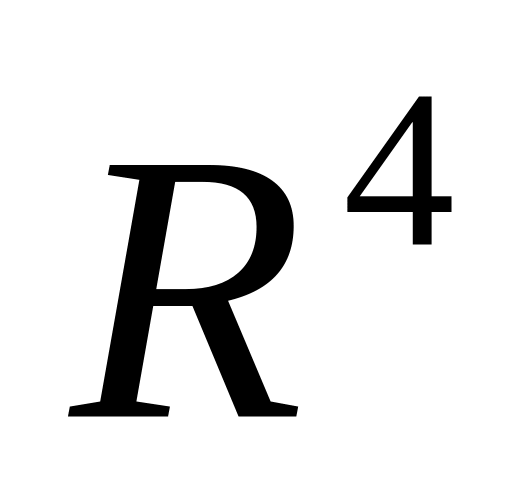 ,
если
,
если
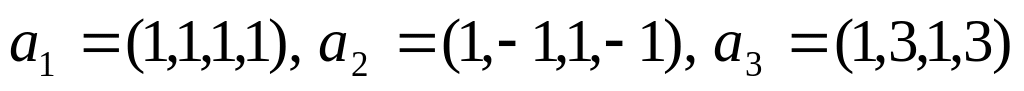 и
и
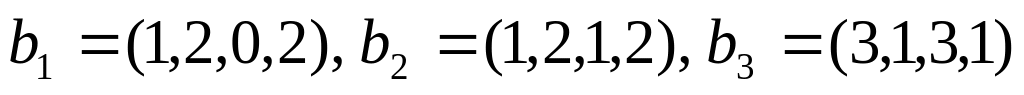 .
Ответ:
.
Ответ:
 .
.
ЗАНЯТИЕ 11. Линейные многообразия.
Найти базис направляющего пространства и вектор сдвига для многообразия M решений системы линейных уравнений:
 Ответ: в записи M=a+L
имеем a=(0,1,1,0) и
Ответ: в записи M=a+L
имеем a=(0,1,1,0) и
 ,
где
,
где
 .
.Выяснить, пересекаются ли в пространстве многообразия
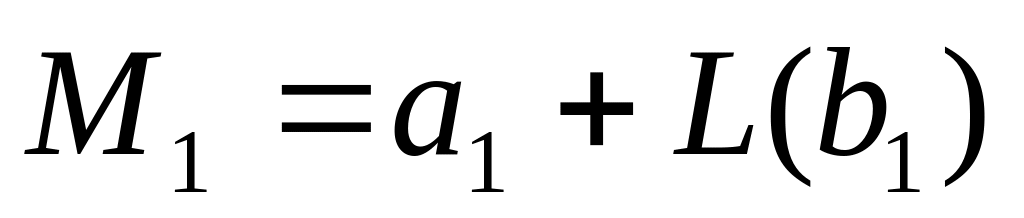 и
и
 ,
где
,
где
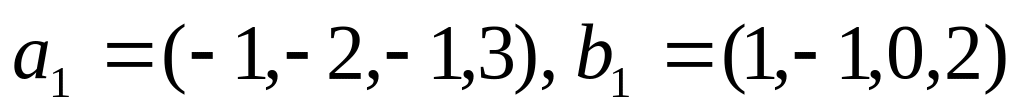 и
и
 .
Ответ:
не пересекаются.
.
Ответ:
не пересекаются.
ЗАНЯТИЯ 12, 13. Процесс ортогонализации.
Ортогонализировать систему векторов пространства :
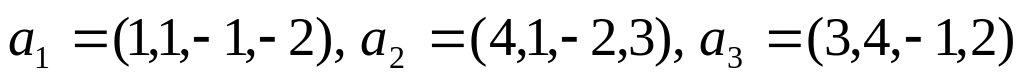 .
Ответ:
.
Ответ:
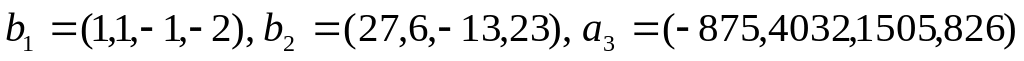 .
.Проверить, что векторы
 ортогональны и нормированы. Дополнить
систему
ортогональны и нормированы. Дополнить
систему
 до ортогонального базиса пространства
.
Ответ:
до ортогонального базиса пространства
.
Ответ:
 .
.Построить ортонормированный базис линейной оболочки векторов
 .
Ответ:
.
Ответ:
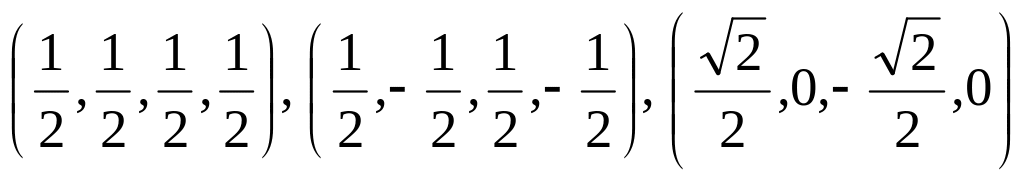 .
.Найти ортонормированный базис пространства решений однородной системы линейных уравнений:
 Ответ:
Ответ:
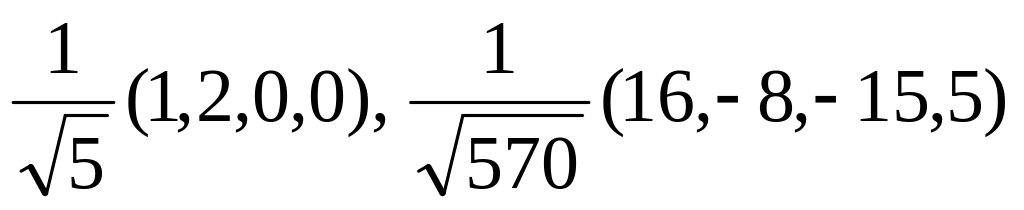 .
.
ЗАНЯТИЕ 14. Ортогональное дополнение.
В пространстве задано подпространство L однородной системой линейных уравнений:
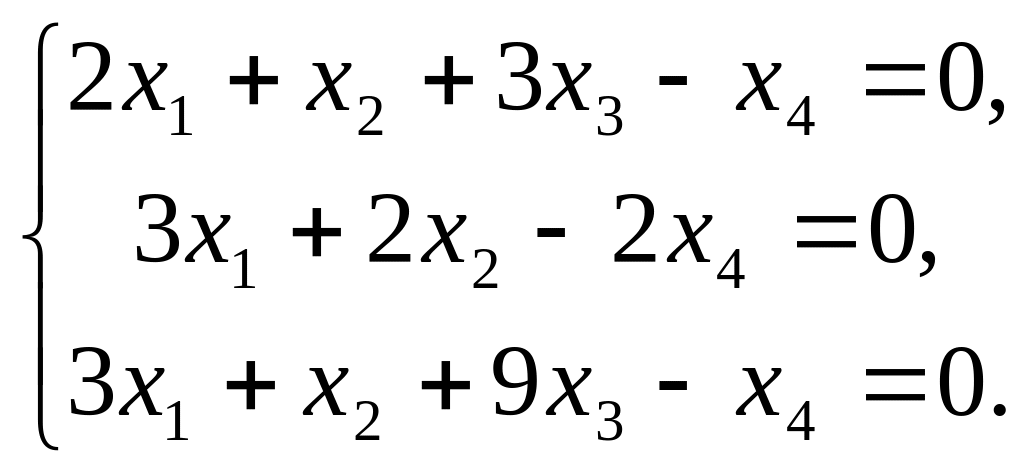 Найти ортогональные базисы в пространствах
Найти ортогональные базисы в пространствах
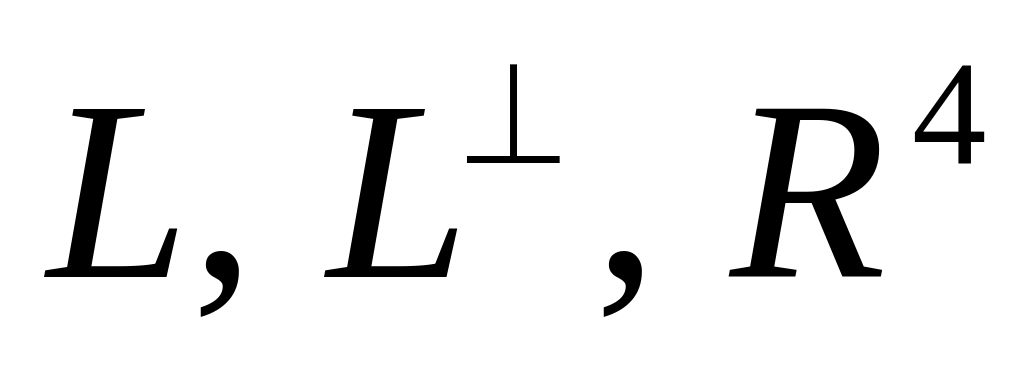 .
.
В пространстве
 найти базис ортогонального дополнения
найти базис ортогонального дополнения
 ,
если само подпространство L
является линейной оболочкой векторов
,
если само подпространство L
является линейной оболочкой векторов
 .
Ответ: например,
.
Ответ: например,
 .
.Найти ортогональную проекцию и ортогональную составляющую вектора x=(3,–5,2,–10) относительно линейной оболочки векторов
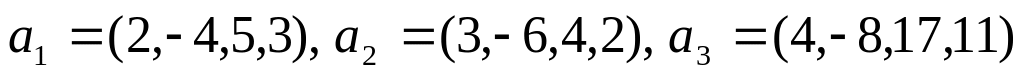 .
Ответ: y=(3,–6,–3,–3),
z=(0,1,5,–7).
.
Ответ: y=(3,–6,–3,–3),
z=(0,1,5,–7).
Модуль 4.
ЗАНЯТИЕ 15, 16. Ядро и образ линейного оператора.
Можно ли с помощью следующих равенств задать линейные операторы пространства ? Для линейных операторов найти их матрицы в базисе (1,0,0), (0,1,0), (0,0,1).
 .
Ответ: можно,
.
Ответ: можно,
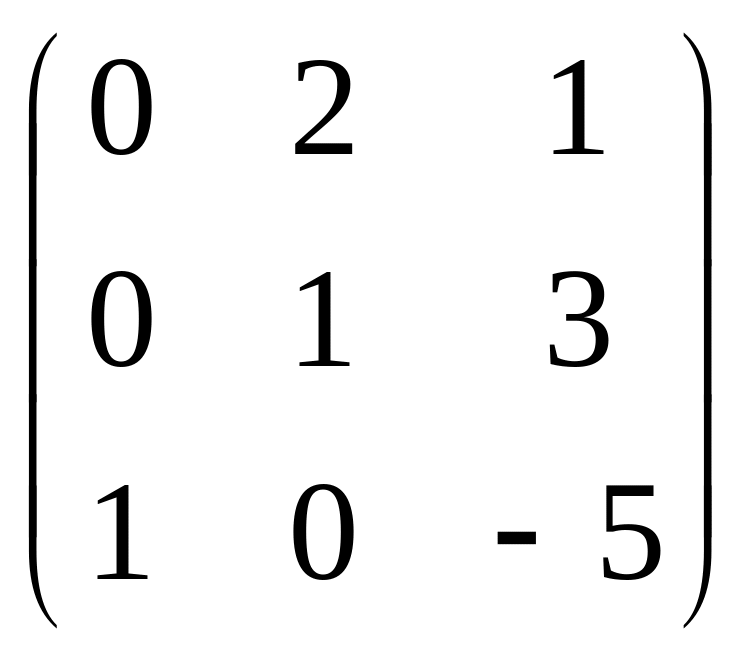 .
. .
Ответ: нельзя.
.
Ответ: нельзя.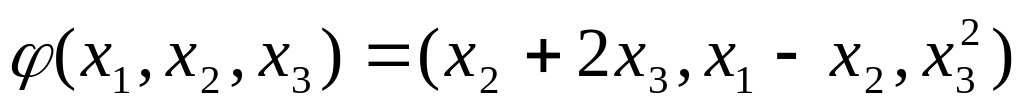 .
Ответ: нельзя.
.
Ответ: нельзя. .
Ответ: можно,
.
Ответ: можно,
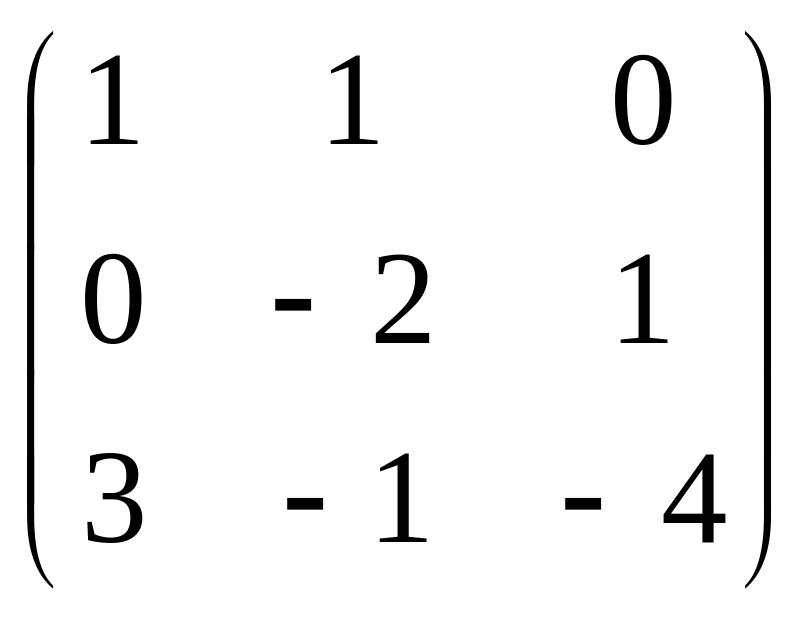 .
.
Можно ли с помощью следующих равенств задать линейные операторы пространства ? Для линейных операторов найти их матрицы в базисе .
 .
Ответ: можно,
.
Ответ: можно,

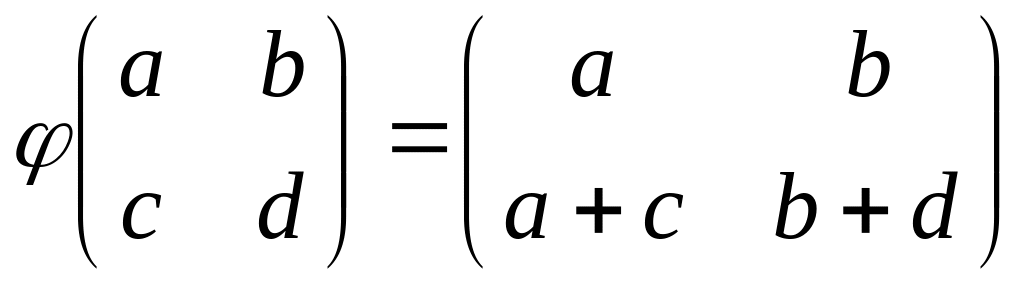 .
Ответ: можно,
.
Ответ: можно,
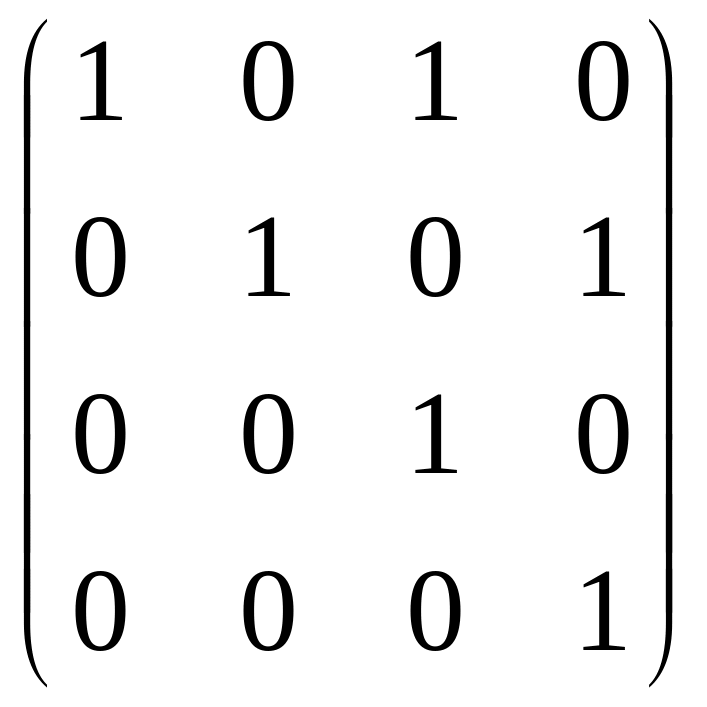
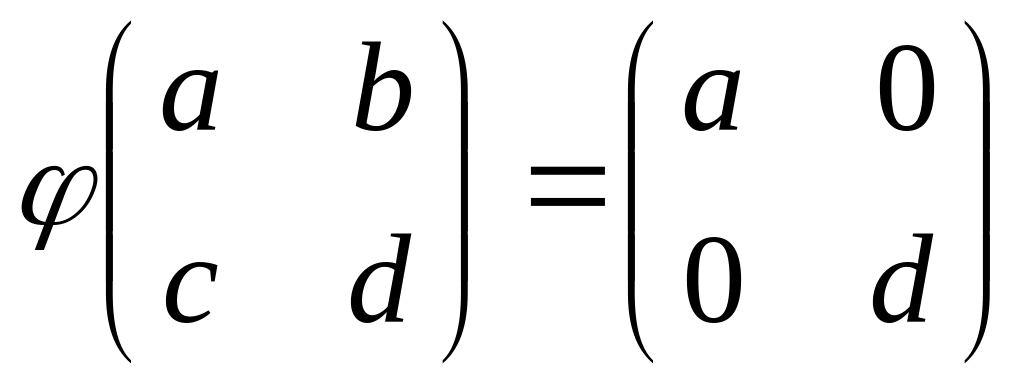 .
Ответ: можно,
.
Ответ: можно,
 .
.
Найти базис ядра и образа линейного оператора φ пространства V, заданного в некотором базисе матрицей:
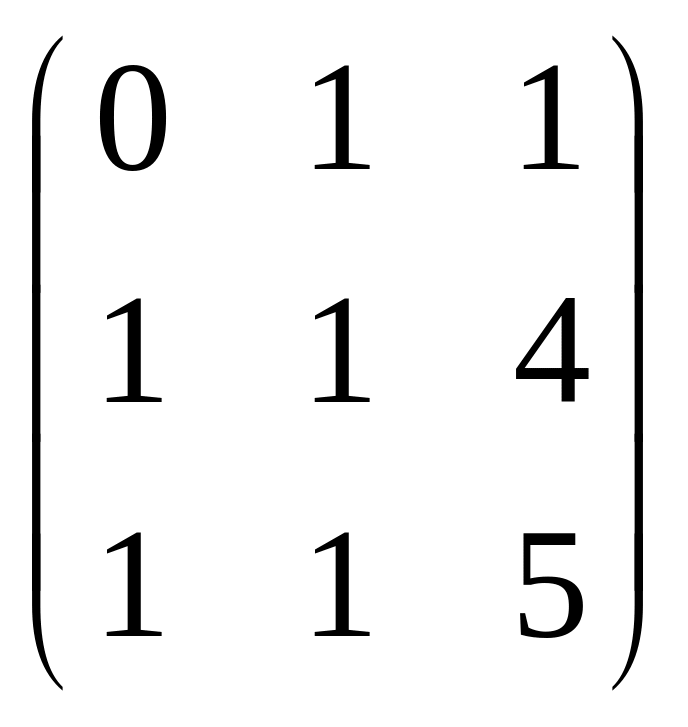 Ответ:
Ответ:
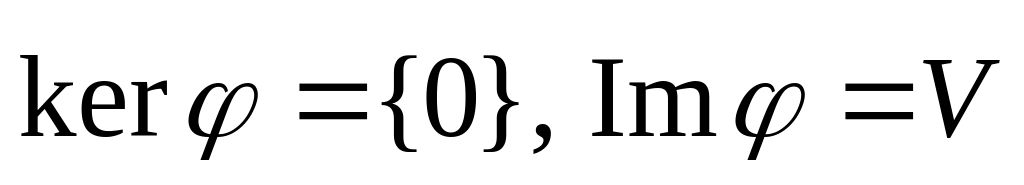 .
. Ответ:
базис Im φ:
Ответ:
базис Im φ:
 ;
базис ker φ:
;
базис ker φ:
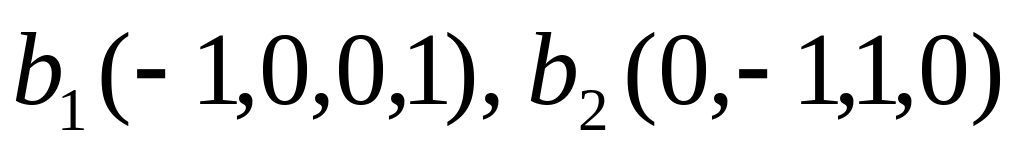 .
.
Найти ранг, дефект, а также базисы ядра и образа линейного оператора φ пространства , заданного условием:
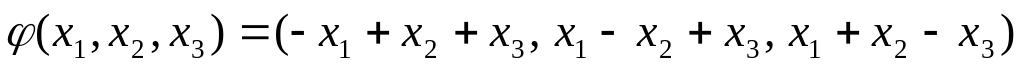 .
Ответ: rang φ=3,
df
φ=0.
.
Ответ: rang φ=3,
df
φ=0.Доказать, что существует линейный оператор пространства , переводящий векторы
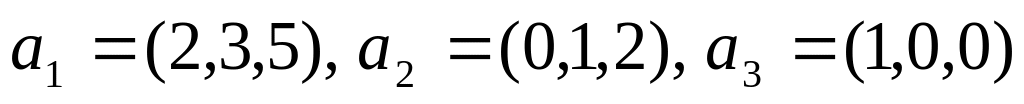 соответственно в векторы
соответственно в векторы
 .
Найти его матрицу в базисе
.
Найти его матрицу в базисе
 .
Ответ:
.
Ответ:
 .
.
ЗАНЯТИЕ 17. Матрица линейного оператора.
Линейный оператор пространства V задан в базисе матрицей
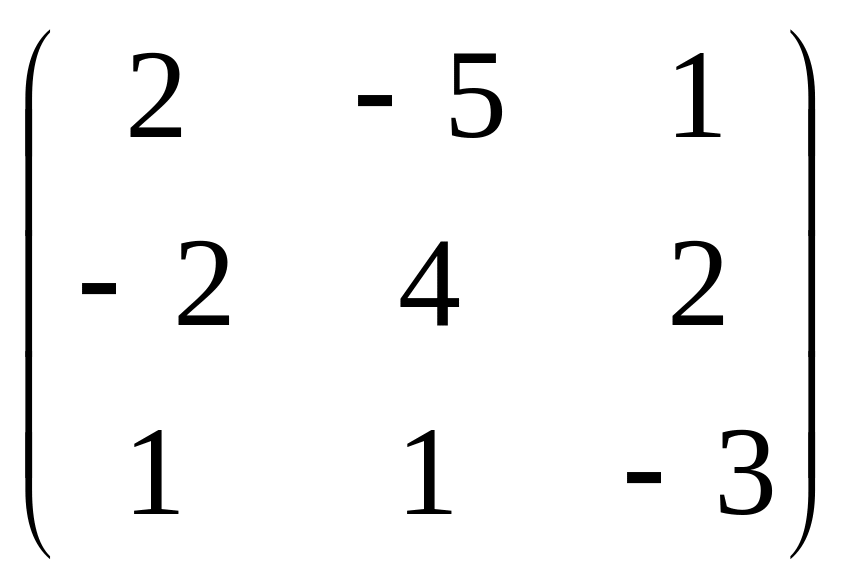 .
Найти образ вектора
.
Найти образ вектора
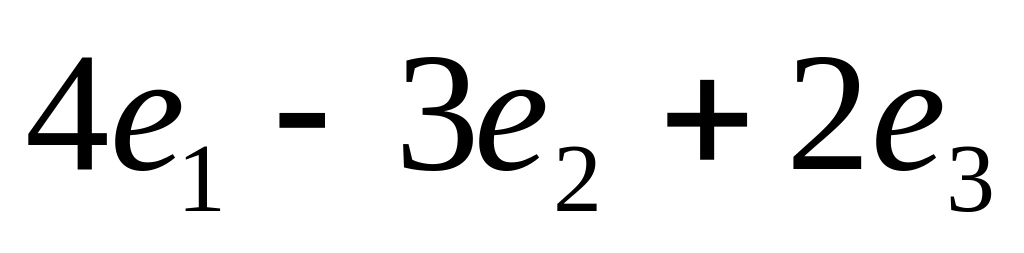 .
Ответ:
.
Ответ:
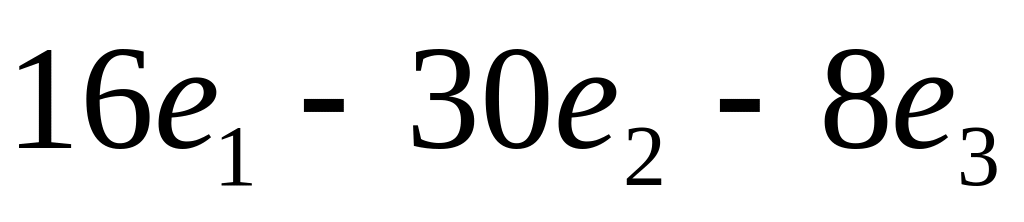 .
.Линейный оператор φ пространства переводит векторы
 соответственно в векторы
соответственно в векторы
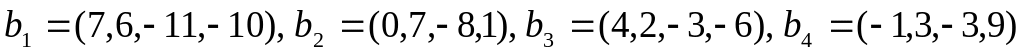 .
Найти его матрицу в базисе
.
Ответ:
.
Найти его матрицу в базисе
.
Ответ:
 .
.Линейный оператор φ пространства V задан в базисе матрицей
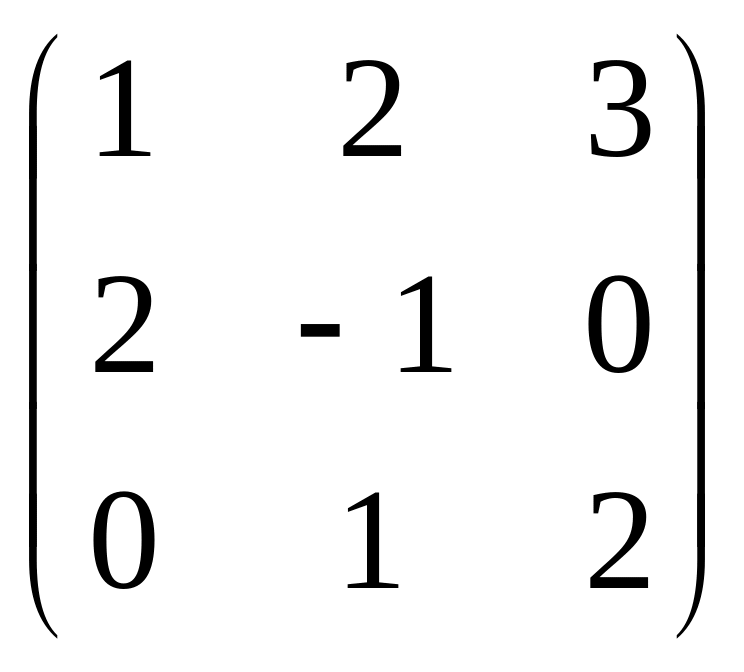 .
Найти его матрицу в базисе
.
Найти его матрицу в базисе
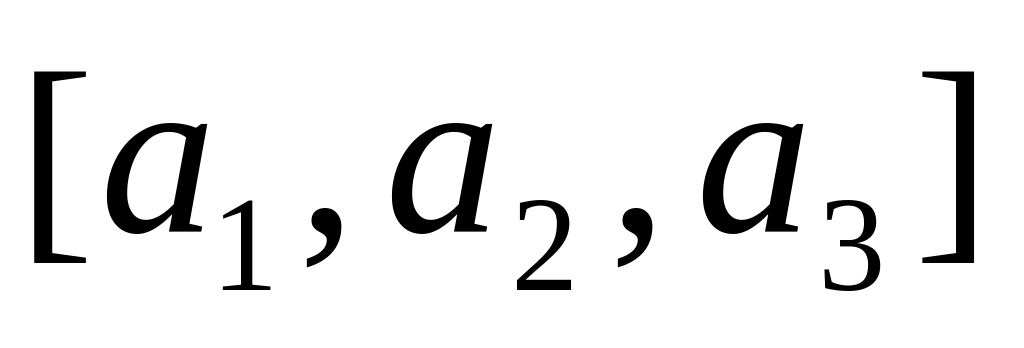 ,
если
,
если
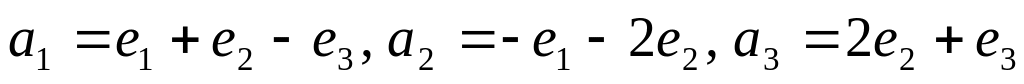 .
Ответ:
.
Ответ:
 .
.Линейный оператор φ в базисе
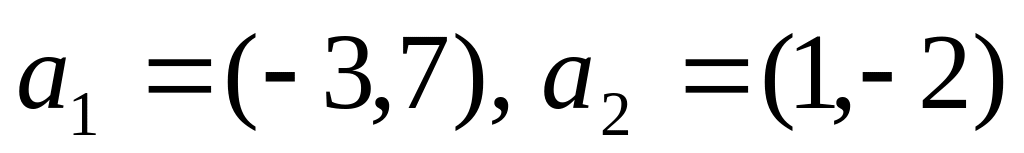 имеет матрицу
имеет матрицу
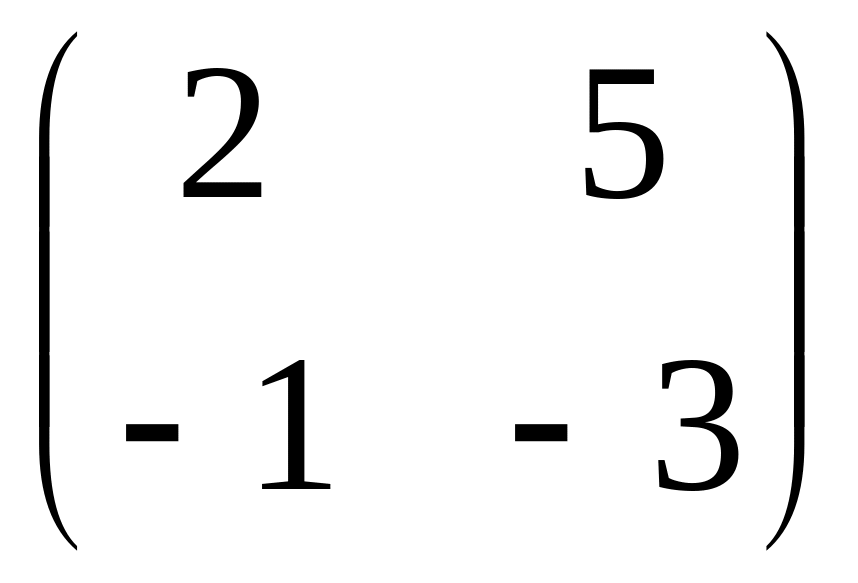 ,
а линейный оператор ψ в базисе
,
а линейный оператор ψ в базисе
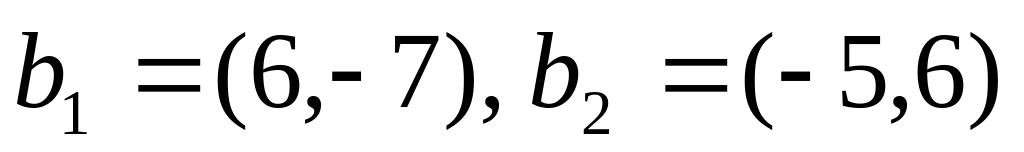 матрицу
матрицу
 .
Найти матрицу линейного оператора φψ
в базисе
.
Найти матрицу линейного оператора φψ
в базисе
 .
Ответ:
.
Ответ:
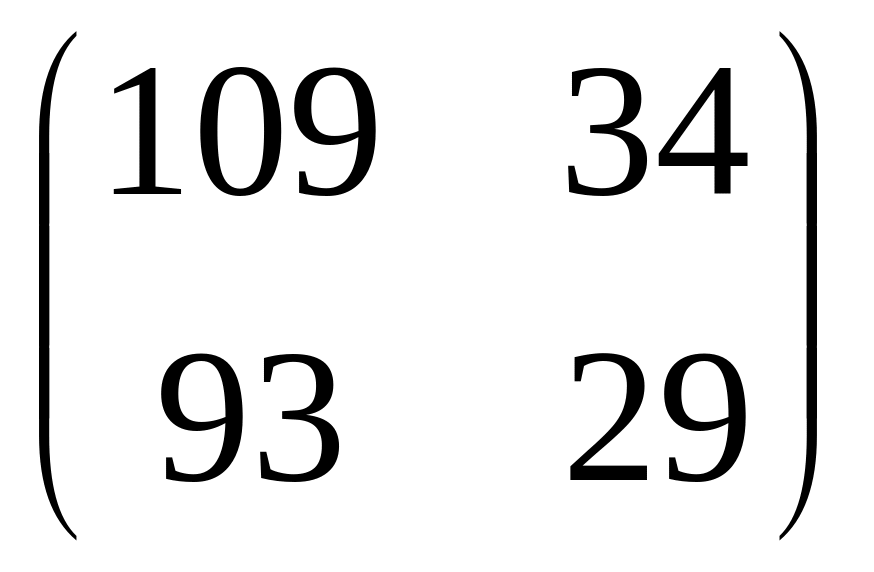 .
.
ЗАНЯТИЕ 18. Собственные векторы и собственные значения линейного оператора.
Найти собственные векторы и собственные значения линейных операторов пространства , заданных в некотором базисе матрицами:
 .
Ответ:
.
Ответ:
 ,
e=(1,0,1).
,
e=(1,0,1).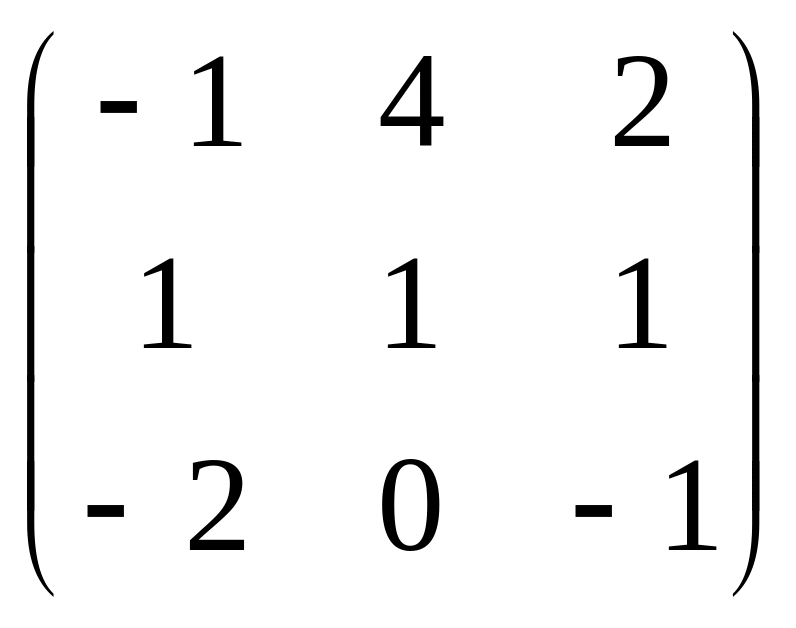 .
Ответ:
.
Ответ:
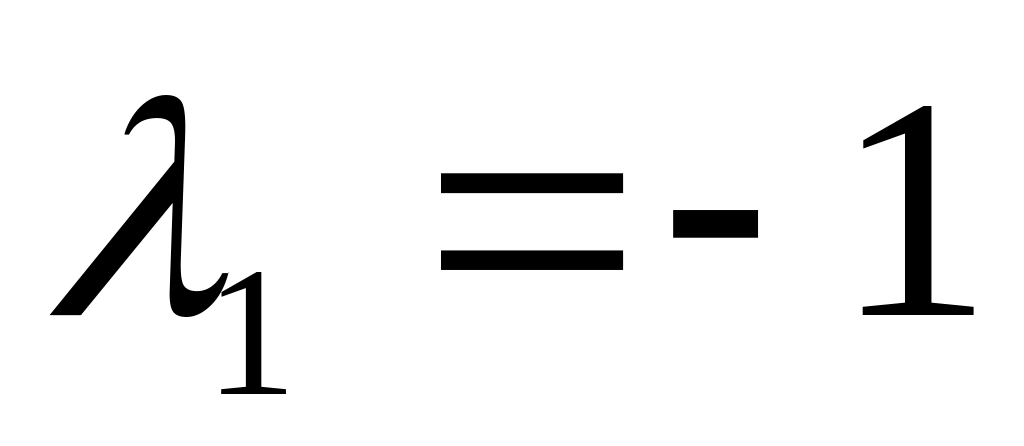 ,
,
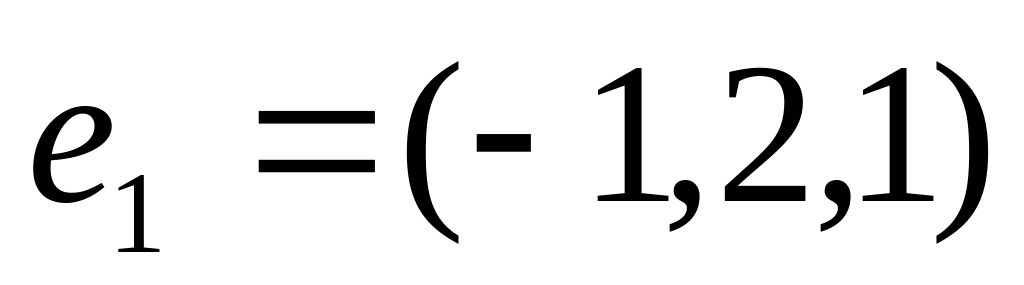 ,
,
 ,
,
 .
. .
Ответ:
.
Ответ:
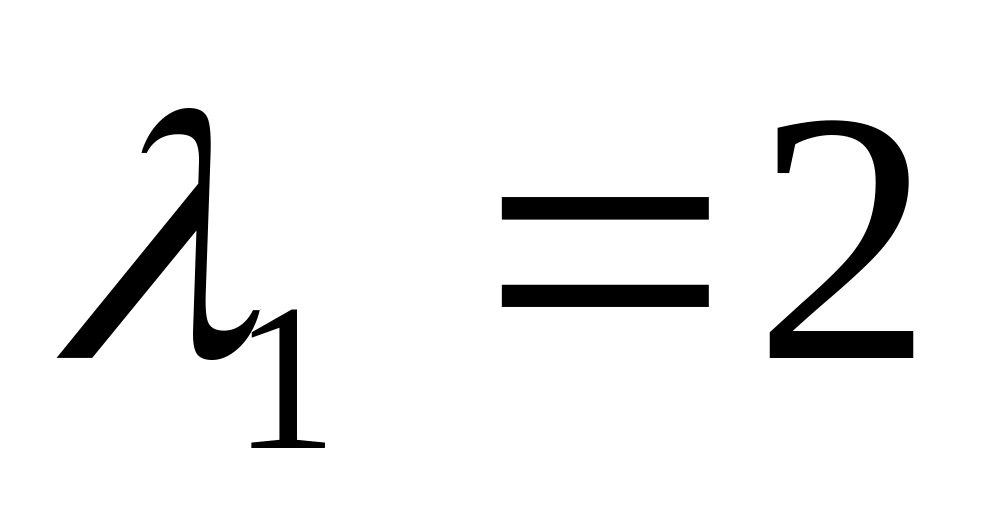 ,
,
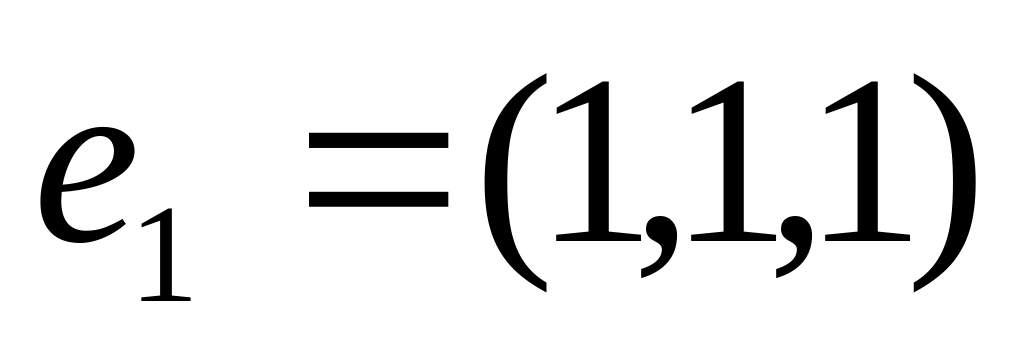 ,
,
 ,
,
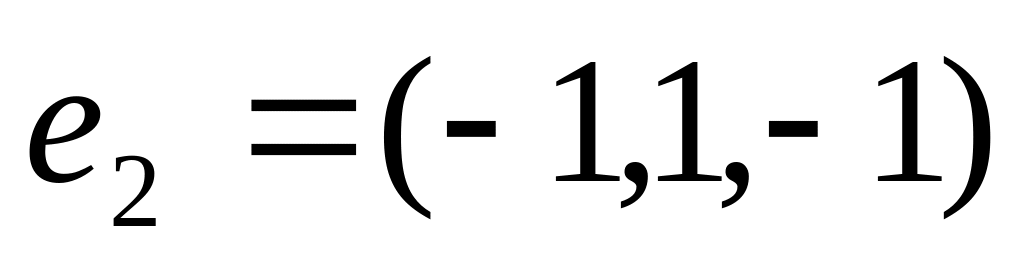 ,
,
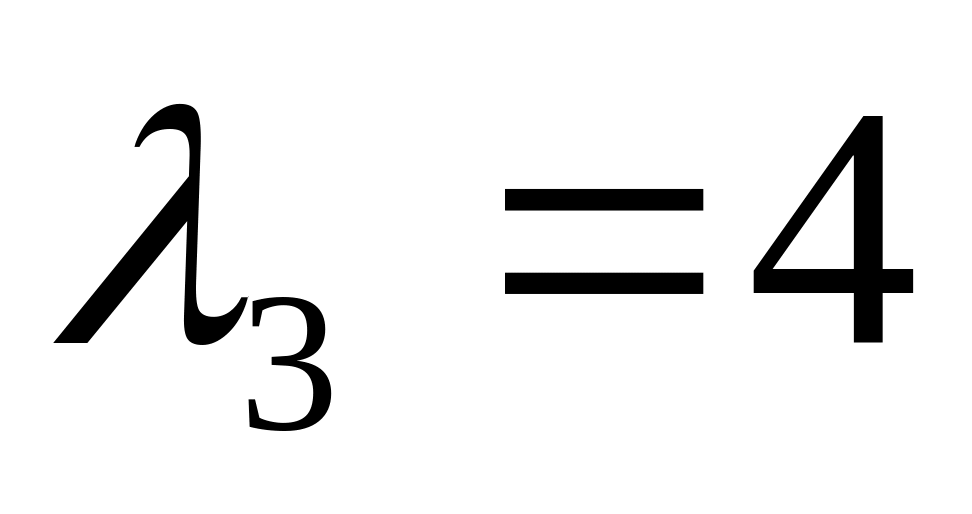 ,
,
 .
. .
Ответ:
.
Ответ:
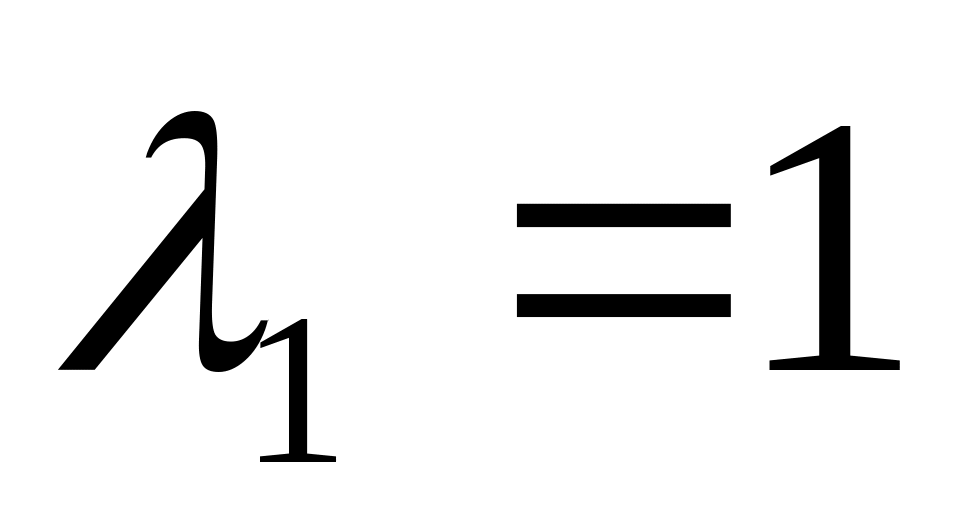 ,
,
 ,
,
 ,
,
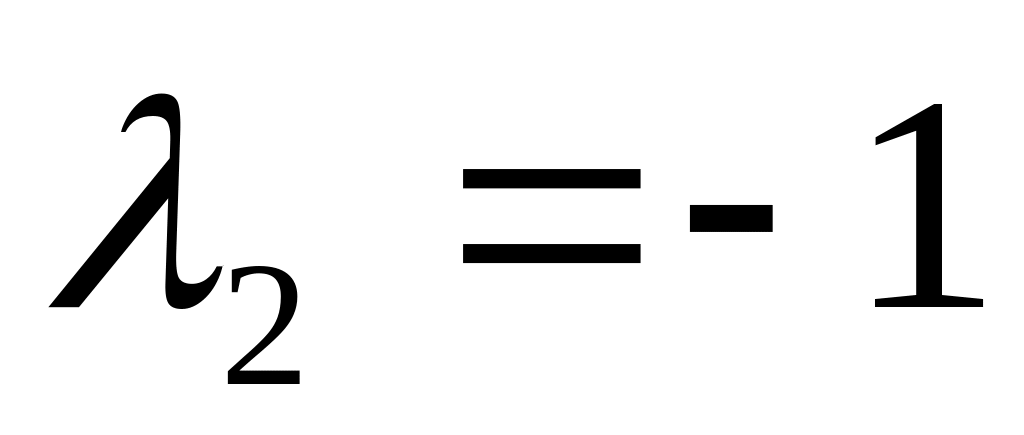 ,
,
 .
.
Подобна ли матрица диагональной:
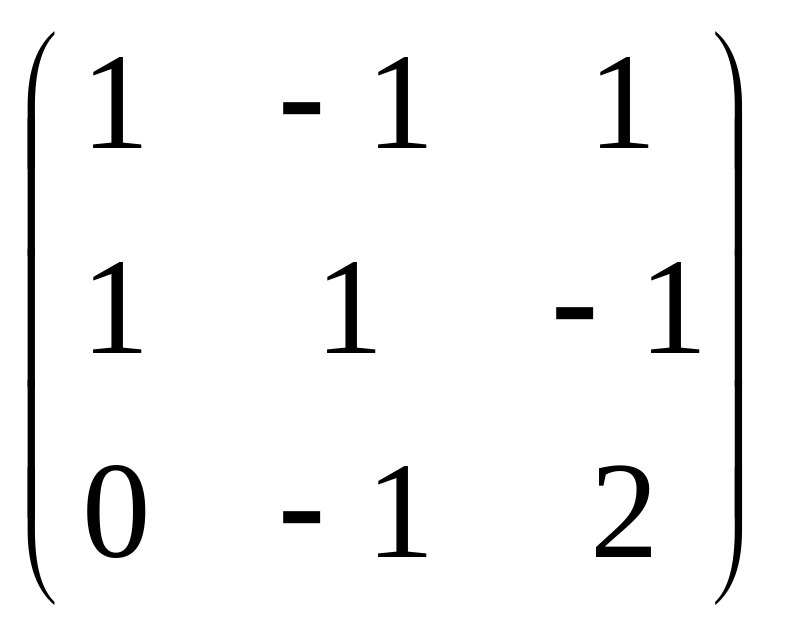 Ответ: нет.
Ответ: нет.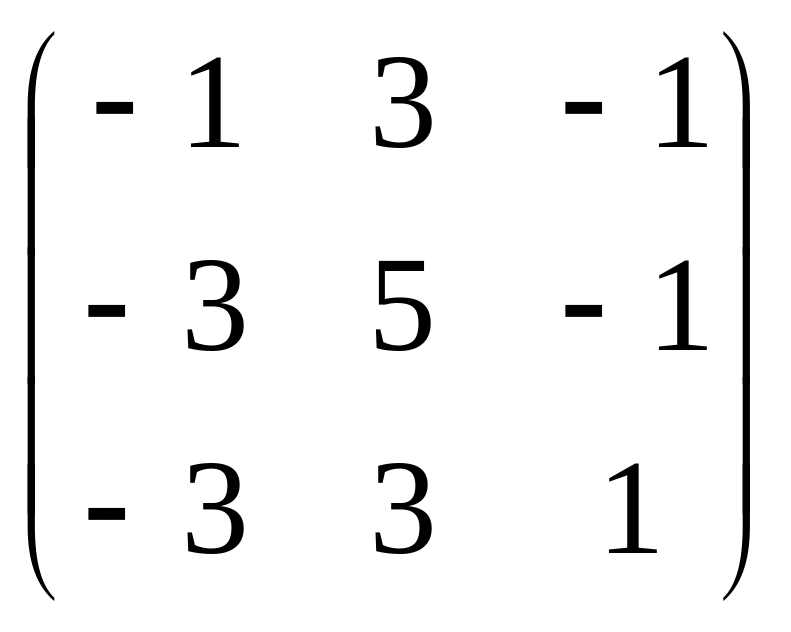 Ответ: подобна матрице
Ответ: подобна матрице
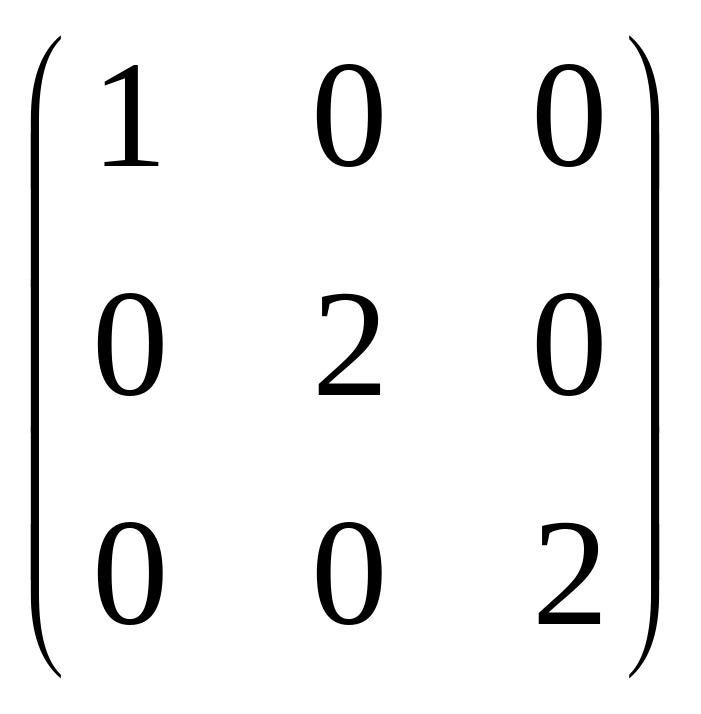 .
.
Департамент образования города Москвы
Государственное образовательное учреждение
высшего профессионального образования города Москвы
«МОСКОВСКИЙ ГОРОДСКОЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»
Институт математики и информатики
Математический факультет
![]()
Наименование дисциплины / курса |
Уровень образования |
Статус дисциплины в рабочем учебном плане |
Количество зачетных единиц |
Форма отчетности |
Курс, семестр |
Алгебра 2 |
Бакалавриат |
Б3 вариативная часть |
3 |
зачет |
1 курс бакалавриата, 2 семестр |
Модуль 1. |
||||
Тема или задание текущей аттестационной работы |
Виды текущей аттестации |
Аудиторная или внеаудиторная |
Минимальное количество баллов |
Максимальное количество баллов |
Посещение лекционных и семинарских занятий, дисциплинированность, культура поведения |
Посещаемость (на каждом занятии 1 балл) |
Аудиторная |
- |
2 |
Ведение записей лекций – академическая компетенция |
Проверка и анализ конспектов (выборочно, произвольно) |
Аудиторная |
- |
3 |
Активная работа на практических занятиях, выполнение домашних заданий – академическая и коммуникативная компетенция |
Выступления, проверка домашних заданий |
Аудиторная и внеаудиторная |
- |
5 |
Выполнение контрольной работы– академическая компетенция |
Письменная работа, собеседование. |
Внеаудиторная |
- |
8 |
Коллоквиум по материалу модуля |
Коллоквиум |
Аудиторная |
- |
4 |
Итого |
|
|
- |
22 |
Модуль 2. |
||||
Тема или задание текущей аттестационной работы |
Виды текущей аттестации |
Аудиторная или внеаудиторная |
Минимальное количество баллов |
Максимальное количество баллов |
Посещение лекционных и семинарских занятий, дисциплинированность, культура поведения |
Посещаемость (на каждом занятии 1 балл) |
Аудиторная |
- |
2 |
Ведение записей лекций – академическая компетенция |
Проверка и анализ конспектов (выборочно, произвольно) |
Аудиторная |
- |
3 |
Активная работа на практических занятиях, выполнение домашних заданий – академическая и коммуникативная компетенция |
Выступления, проверка домашних заданий |
Аудиторная и внеаудиторная |
- |
5 |
Выполнение контрольной работы– академическая компетенция |
Письменная работа, собеседование. |
Внеаудиторная |
- |
8 |
Коллоквиум по материалу модуля |
Коллоквиум |
Аудиторная |
- |
4 |
Итого |
|
|
- |
22 |
Модуль 3. |
||||
Тема или задание текущей аттестационной работы |
Виды текущей аттестации |
Аудиторная или внеаудиторная |
Минимальное количество баллов |
Максимальное количество баллов |
Посещение лекционных и семинарских занятий, дисциплинированность, культура поведения |
Посещаемость (на каждом занятии 1 балл) |
Аудиторная |
- |
3 |
Ведение записей лекций – академическая компетенция |
Проверка и анализ конспектов (выборочно, произвольно) |
Аудиторная |
- |
4 |
Активная работа на практических занятиях, выполнение домашних заданий – академическая и коммуникативная компетенция |
Выступления, проверка домашних заданий |
Аудиторная и внеаудиторная |
- |
6 |
Выполнение контрольной работы– академическая компетенция |
Письменная работа, собеседование. |
Внеаудиторная |
- |
10 |
Коллоквиум по материалу модуля |
Коллоквиум |
Аудиторная |
- |
5 |
Итого |
|
|
- |
28 |
Модуль 4. |
||||
Тема или задание текущей аттестационной работы |
Виды текущей аттестации |
Аудиторная или внеаудиторная |
Минимальное количество баллов |
Максимальное количество баллов |
Посещение лекционных и семинарских занятий, дисциплинированность, культура поведения |
Посещаемость (на каждом занятии 1 балл) |
Аудиторная |
- |
3 |
Ведение записей лекций – академическая компетенция |
Проверка и анализ конспектов (выборочно, произвольно) |
Аудиторная |
- |
4 |
Активная работа на практических занятиях, выполнение домашних заданий – академическая и коммуникативная компетенция |
Выступления, проверка домашних заданий |
Аудиторная и внеаудиторная |
- |
6 |
Выполнение контрольной работы– академическая компетенция |
Письменная работа, собеседование. |
Внеаудиторная |
- |
10 |
Коллоквиум по материалу модуля |
Коллоквиум |
Аудиторная |
- |
5 |
Итого |
|
|
- |
28 |
Итого максимум |
100 |
Необходимый минимум для допуска к промежуточной аттестации 41 балл.
Дополнительные требования для студентов, отсутствующих на занятиях по уважительной причине: устное или письменное собеседование по тематике пропущенных занятий, выполнение заданий практических занятий, выполнение контрольных и письменных работ.
Форма промежуточной аттестации: зачет – максимальное количество баллов 20 дополнительно к набранным.
Таблица соответствия с пятибалльной системой оценки знаний
Баллы |
0 ‑ 40 |
41 ‑ 60 |
61 ‑ 80 |
81 ‑ 100 |
Оценка |
Неудовлетворительно |
Удовлетворительно |
Хорошо |
Отлично |
