
- •Программа курса «элементарная математика (планиметрия)»
- •1. Содержание дисциплины и ее разделы
- •2. Учебно-методическое и информационное обеспечение дисциплины литература
- •3. Методические рекомендации и план освоения учебной дисциплины календарно-тематический план освоения дисциплины
- •План практических занятий Модуль 1. Треугольник.
- •Модуль 2. Четырехугольники.
- •Модуль 3. Окружность и круг.
- •Государственное образовательное учреждение
Программа курса «элементарная математика (планиметрия)»
Направление «Педагогическое образование», профиль «Математика», первый курс, второй семестр, 2011/12 уч. год, 36 часов практических занятий, 3 контрольные работы, зачет.
Преподаватель: доц., к.ф-м.н. Ушаков Андрей Владимирович.
1. Содержание дисциплины и ее разделы
Модуль 1. Треугольники. Метрические соотношения между элементами треугольника. Медианы, биссектрисы и высоты треугольника. Вписанный и описанный треугольник. Равнобедренный и прямоугольный треугольник.
Модуль 2.. Четырехугольники. Трапеция. Дополнительные построения, связанные с трапецией. Вписанная и описанная трапеция. Параллелограмм. Признаки параллелограмма. Ромб. Прямоугольник. Квадрат.
Модуль 3. Окружность и круг. Взаиморасположение окружностей. Касательные и секущие. Углы, связанные с окружностью. Длина дуги окружности. Площадь круга, сегмента и сектора. Многоугольники. Правильные многоугольники.
2. Учебно-методическое и информационное обеспечение дисциплины литература
Л.С. Атанасян. Геометрия 7 – 9. М.: Просвещение, 1998.
Л.С. Атанасян, Н.С. Денисова, Е.В. Силаев. Курс элементарной геометрии. Часть 1. Планиметрия. М.: 1992.
И.Ф. Шарыгин. Решение задач 10. М.: Просвещение, 1994.
В.В. Прасолов. Задачи по планиметрии. Часть 1. М.: Наука, 1991.
П.С. Моденов. Задачи по геометрии. М.: Наука, 1979.
З.А. Скопец. Геометрические миниатюры. М.: Просвещение, 1990.
3. Методические рекомендации и план освоения учебной дисциплины календарно-тематический план освоения дисциплины
№ |
Тема |
Общая трудоемкость |
Самостоятельная работа |
Всего аудиторных часов |
Практические и семинарские занятия часов |
Контроль самостоятельной работы |
1 |
Модуль 1. Треугольники. |
22 |
4 |
12 |
12 |
6 |
2 |
Модуль 2. Четырехугольники. |
15 |
3 |
8 |
8 |
5 |
3 |
Модуль 3. Окружность и круг. |
30 |
5 |
16 |
16 |
8 |
4 |
Форма промежуточной аттестации – зачет. |
5 |
|
|
|
|
5 |
Итого за семестр (часов) |
72 (2 зач. ед.) |
12 |
36 |
36 |
19 |
План практических занятий Модуль 1. Треугольник.
ЗАНЯТИЯ 1, 2. Медианы и биссектрисы и высоты треугольника.
В классе:
Медианы треугольника равны 3, 4, 5. Найти площадь этого треугольника. Ответ: 8.
Определить площадь треугольника, если две его стороны равны 1 и
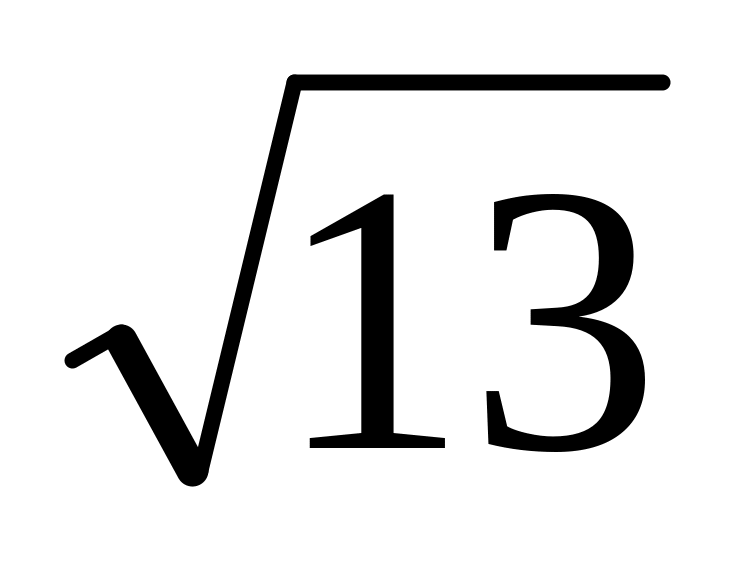 ,
а медиана третьей стороны равна 2. Ответ:
,
а медиана третьей стороны равна 2. Ответ:
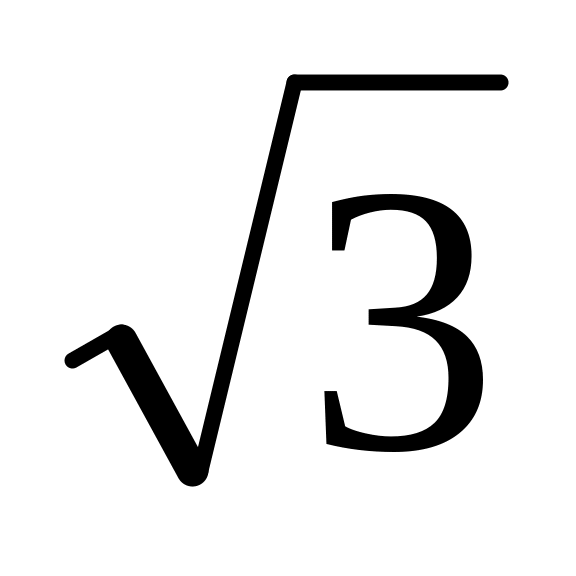 .
.Основание треугольника равно 14. Медианы, проведенные к его боковым сторонам равны
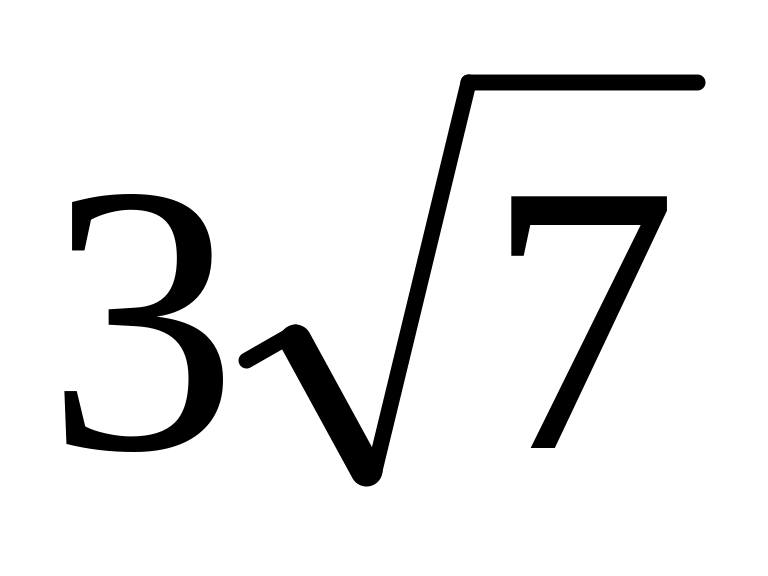 и
и
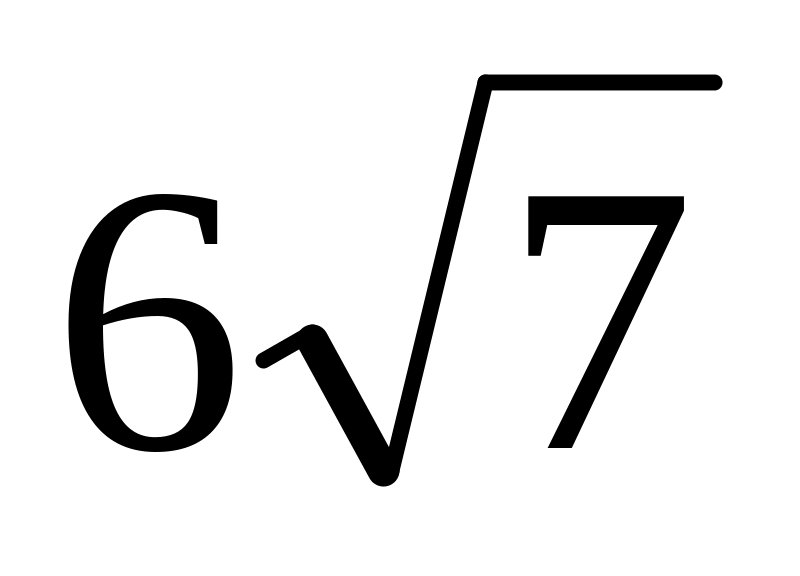 .
Найти боковые стороны этого
треугольника.
Ответ:
.
Найти боковые стороны этого
треугольника.
Ответ:
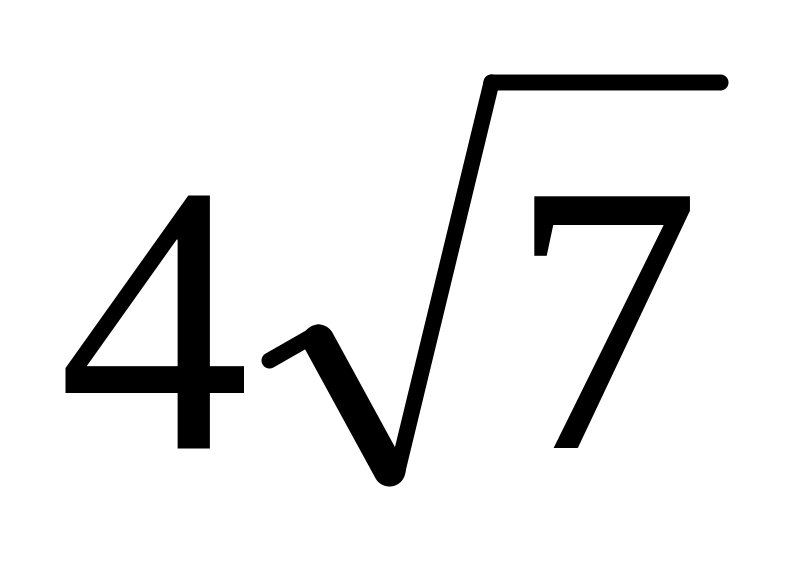 и
и
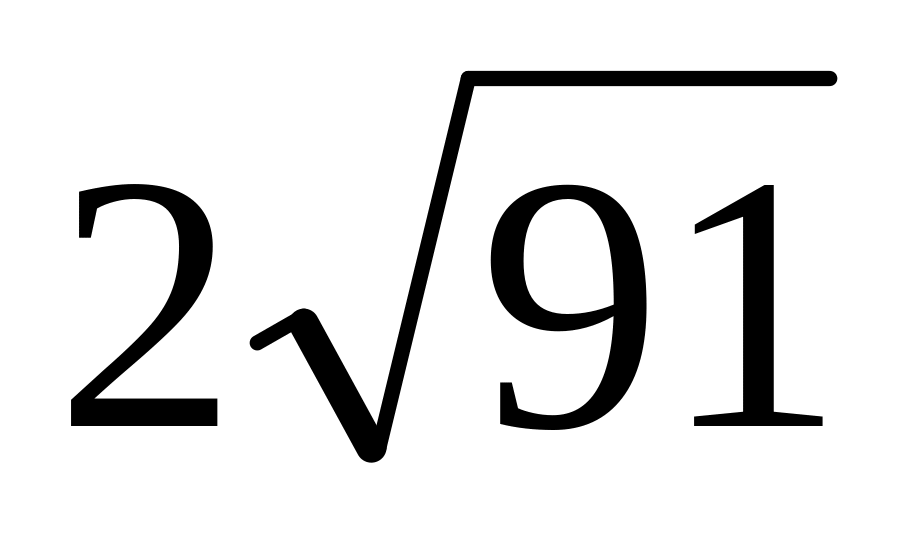 .
.Дан треугольник со сторонами 4, 8, 9. Найти длину биссектрисы, проведенной к его большей стороне. Ответ
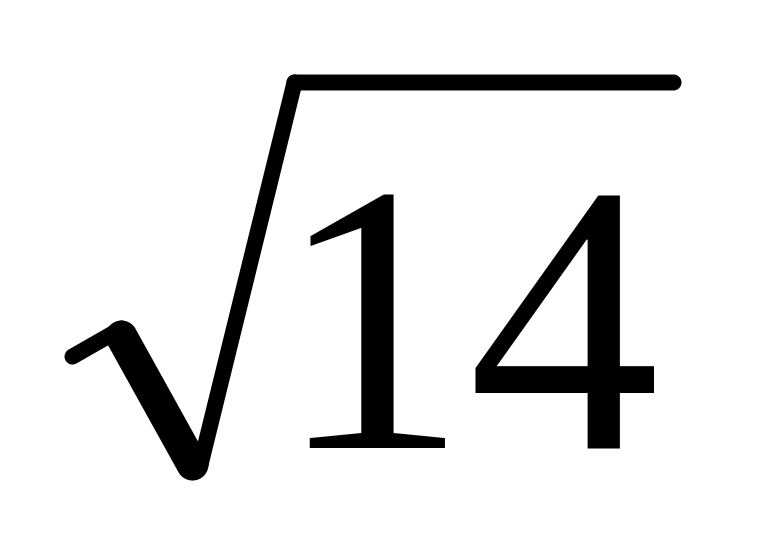 .
.В треугольнике ABC проведена биссектриса BE, которую центр O вписанной окружности делит в отношении BO:OE=2:1. Найти AB, если AC=7 и BC=8. Ответ: 6.
Дан треугольник АВС. Известно, что АВ=4, АС=2 и ВС=3. Биссектриса угла ВАС пересекает сторону ВС в точке К. Прямая, проходящая через точку В параллельно АС, пересекает продолжение биссектрисы АК в точке М. Найти КМ. Ответ:
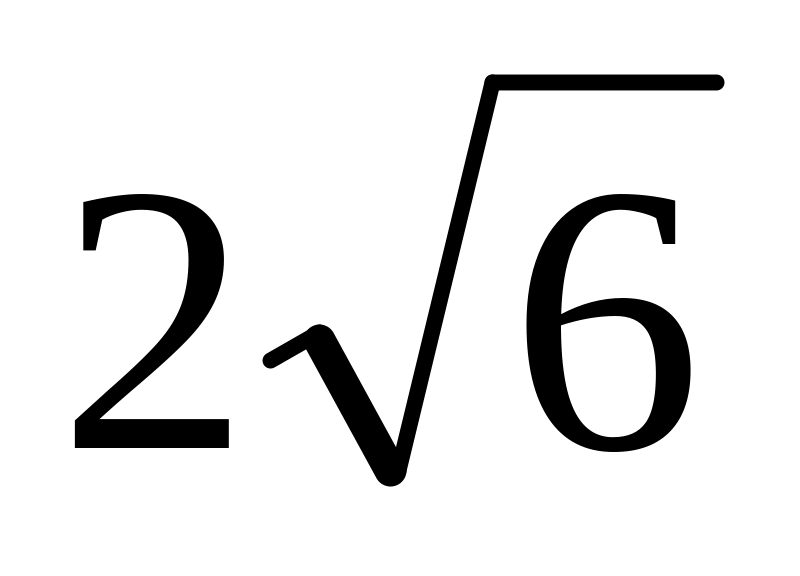 .
.В треугольнике ABC со сторонами AB=12, AC=7 и BC=6 опущены высоты AD и BE. Найти отношение радиусов окружностей, вписанных в треугольники ABC и CDE. Ответ: 84:59.
Наибольшая сторона тупоугольного треугольника равна 3, а высоты, опущенные из вершин его острых углов равны
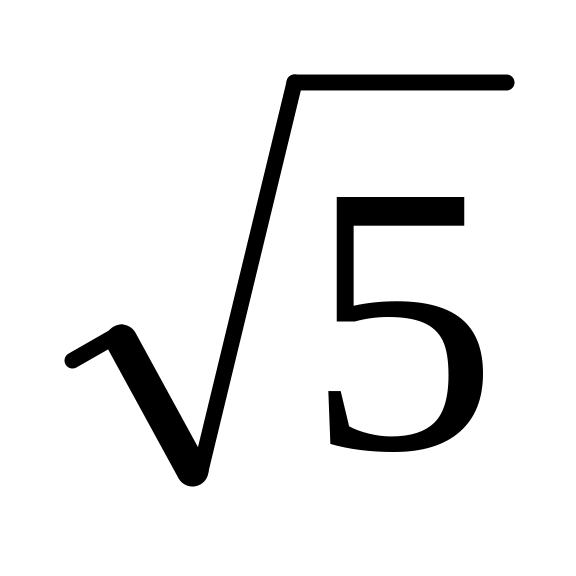 и
и
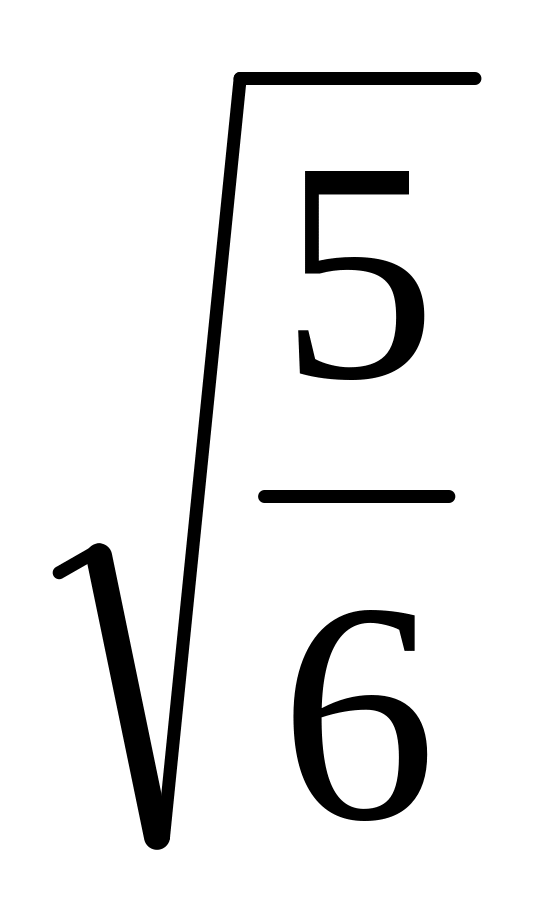 .
Найти две оставшиеся стороны этого
треугольника.
Ответ: 1 и
.
Найти две оставшиеся стороны этого
треугольника.
Ответ: 1 и
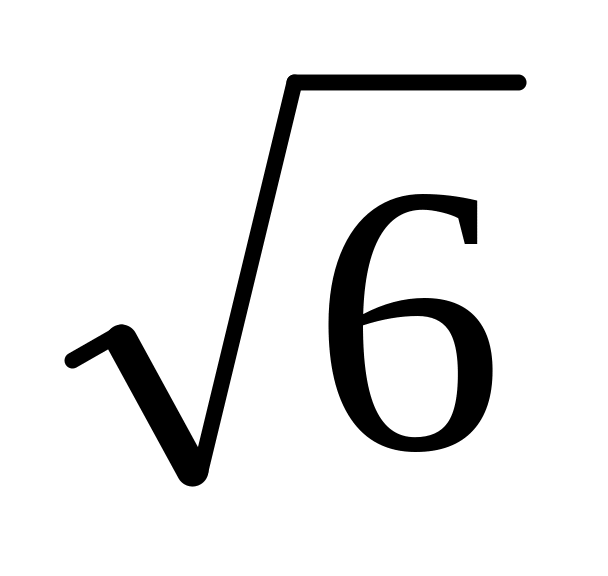 .
.В треугольнике ABC проведены биссектриса CE и высота BD. Найти отношение площадей треугольников ABC и CDE, если AB:BC:AC=3:7:5. Ответ: 24:13.
Точки M и N делят стороны треугольника ABC в отношении AM:MC=3:1 и CN:NB=2:3. Прямые AN и BM пересекаются в точке P. Найти отношение площадей треугольников ABP и ABN. Ответ: 5:6.
Дома:
Основание треугольника равно 26. Медианы его боковых сторон равны 30 и 39. Найти площадь этого треугольника. Ответ: 720.
В треугольнике ABC медианы AD и BE пересекаются под прямым углом. Найти AB, если AC=3 и BC=4. Ответ: .
Одна из сторон треугольника равна 16, а опущенная на нее медиана равна 9. Найти две оставшиеся стороны этого треугольника, если сумма их длин равна 24. Ответ: 11 и 13.
Определить площадь треугольника, если две его стороны равны 35 и 14, а биссектриса угла между ними равна 12. Ответ: 235,2.
В треугольнике АВС проведены биссектрисы CF и AD. Найти отношение площадей треугольников АВС и AFD, если АВ:АС:ВС=21:28:20. Ответ: 4.
Дан треугольник ABC со сторонами
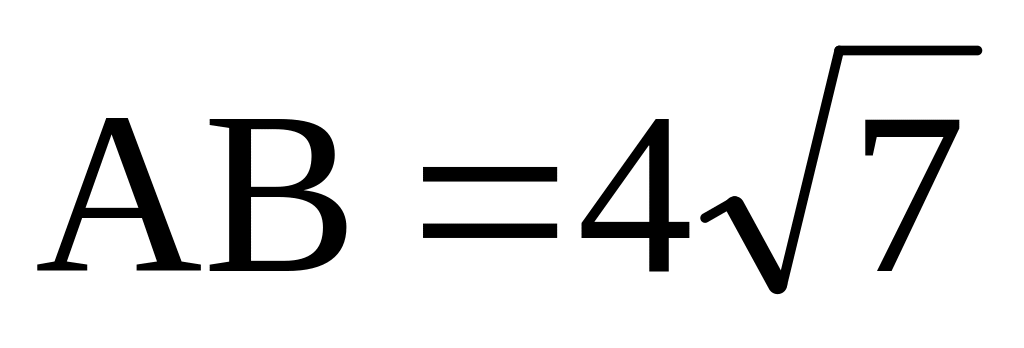 ,
,
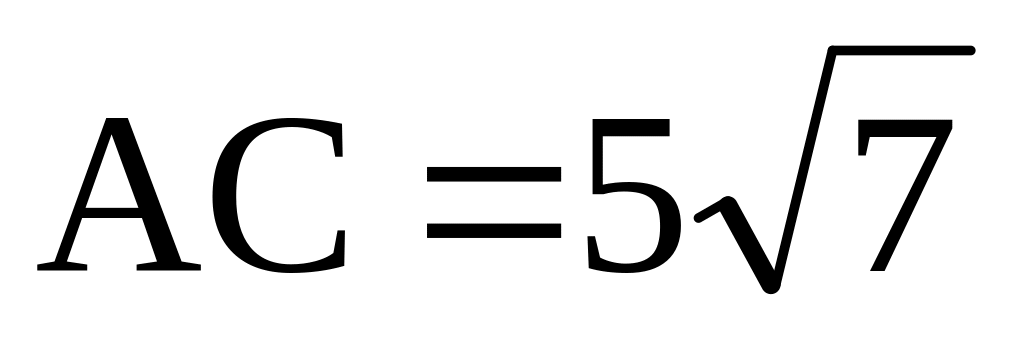 ,
,
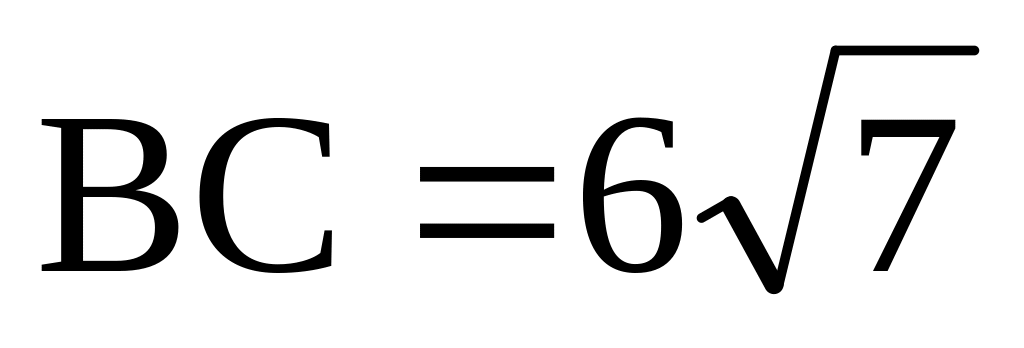 .
Найти расстояние от точки B
до точки пересечения высот треугольника
ABC. Ответ: 9.
.
Найти расстояние от точки B
до точки пересечения высот треугольника
ABC. Ответ: 9.В треугольнике ABC проведены высоты AD и CE. Найти AB, если BE=18, BC=30, AD=20. Ответ: 25.
В остроугольном треугольнике ABC длины медиан BM, CN и высоты AH равны 4, 5 и 6 соответственно. Найти площадь этого треугольника. Ответ:
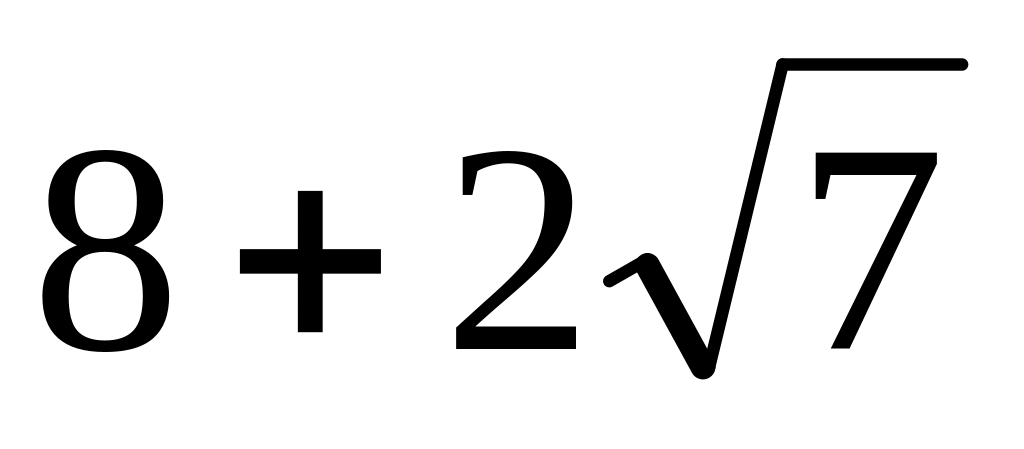 .
.На сторонах AC и BC треугольника ABC взяты точки D и E, так что AD:DC=3:2 и BE:EC=3:4. Прямые AE и BD пересекаются в точке O. Найти отношение BO:OD. Ответ: 5:4.
Найти косинус наибольшего угла треугольника, если синусы двух других его углов равны
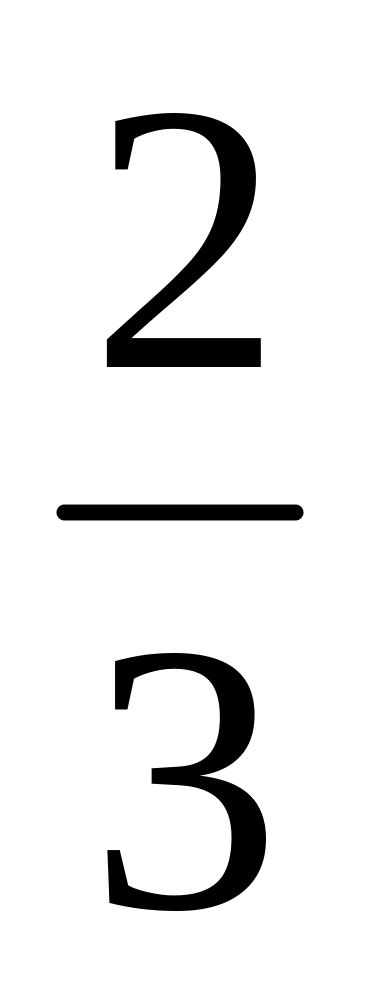 и
и
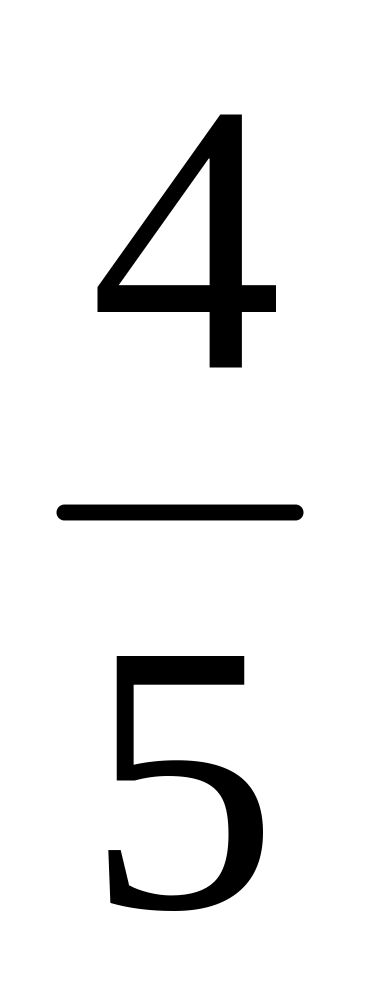 .
Ответ:
.
Ответ:
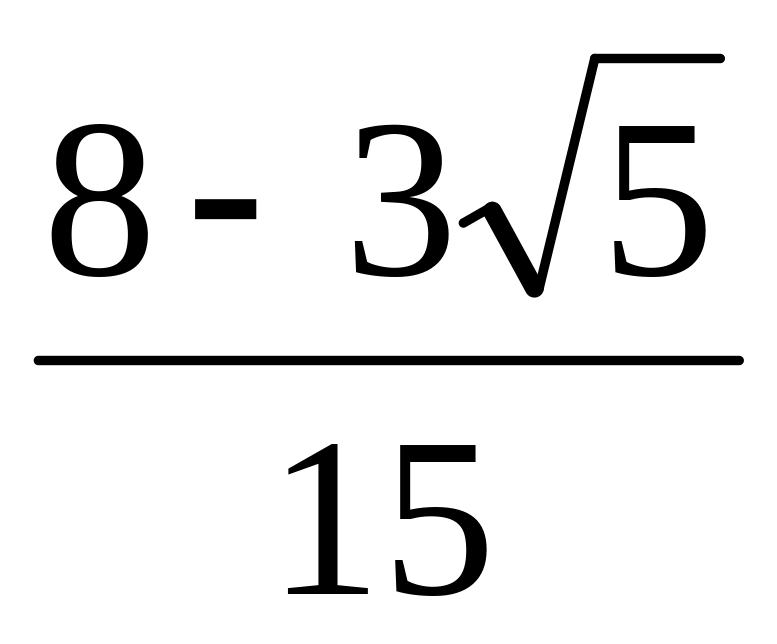 .
.Дан треугольник ABC, у которого
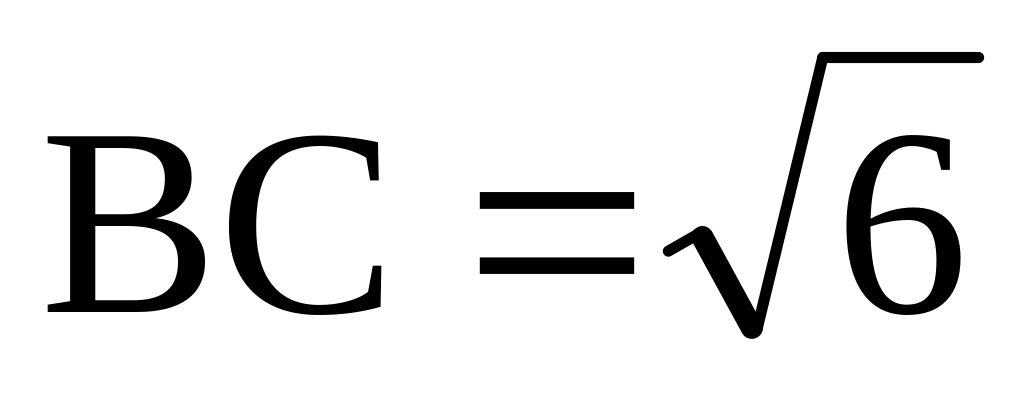 ,
,
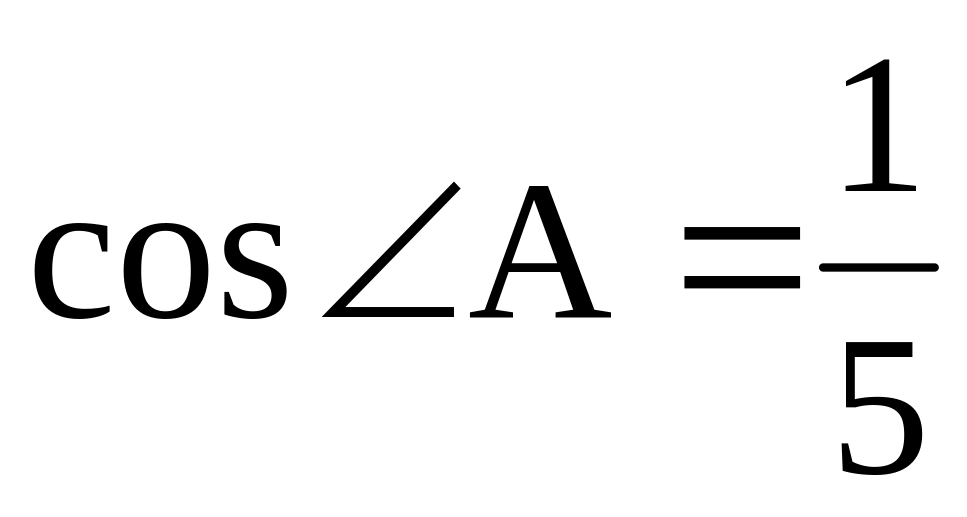 ,
,
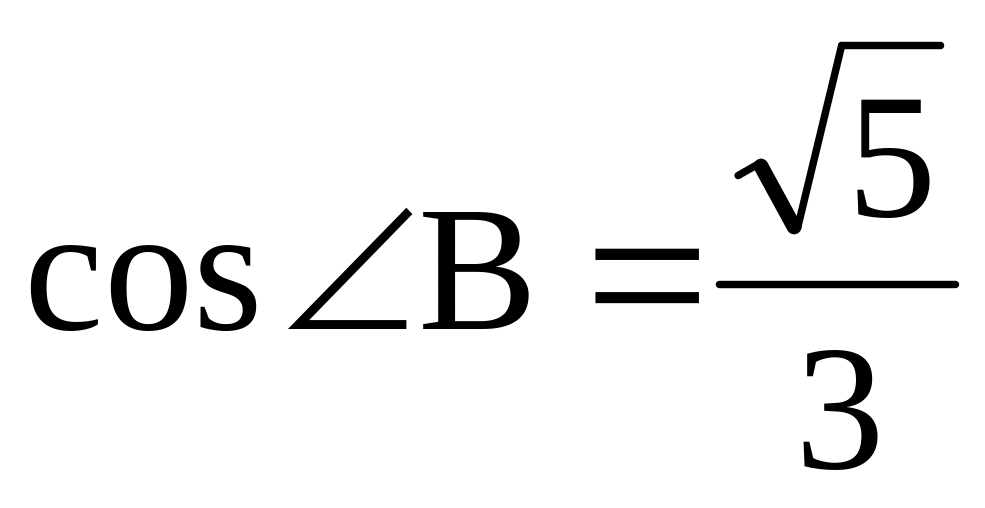 .
Найти AC. Ответ:
.
Найти AC. Ответ:
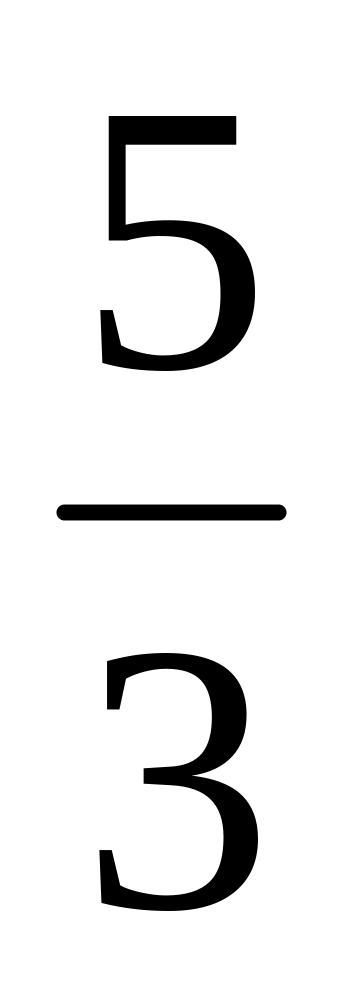 .
.
ЗАНЯТИЯ 3, 4. Вписанный и описанный треугольник.
В классе:
Дан треугольник со сторонами 13, 14, 15. Найти радиусы описанной, вписанной и вневписанных окружностей. Ответ:
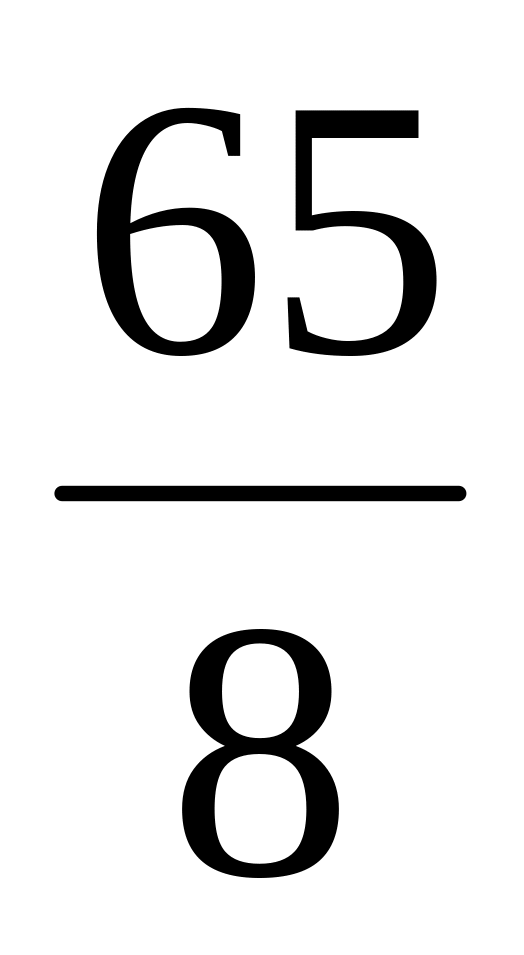 ,
4,
,
4,
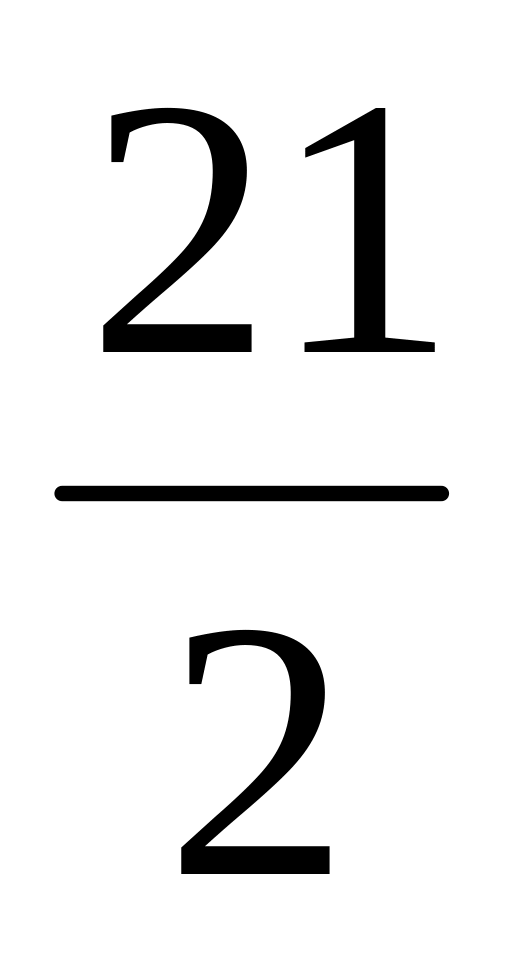 ,
12, 14.
,
12, 14.Длины сторон треугольника пропорциональны числам 4, 13, 15, а радиус описанной около него окружности равен 65. Найти площадь этого треугольника. Ответ: 1536.
Треугольник ABC вписан в окружность радиуса R. Точка D лежит на дуге BC, а хорды AD и BC пересекаются в точке M. Найти BC, если BMD=1200, AB=R, BM:MC=2:3. Ответ:
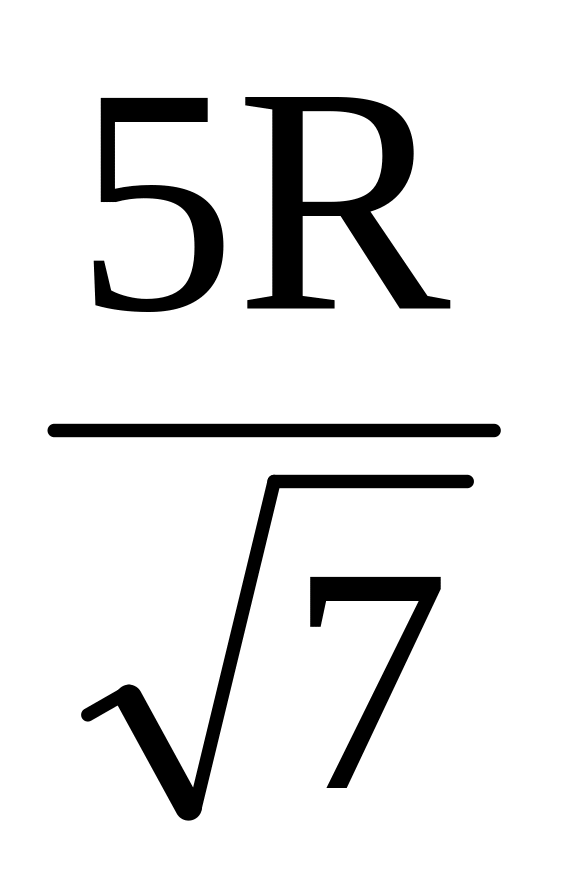 .
.Около треугольника АВС описана окружность. Медиана AD продолжена до пересечения с этой окружностью в точке Е. Известно, что АВ+AD=DE, BAD=600, АЕ=6. Найти площадь треугольника АВС.
На сторонах AB и BC треугольника ABC взяты точки D и E. Точки A, C, D, E лежат на окружности единичного радиуса. Известно, что ABC=300, AC= , BE:EC=2:1. Найти BE. Ответ: 2.
Найти площадь треугольника, вписанного в окружность, если расстояния от концов его стороны равной 20 до касательной, проведенной через противоположную вершину, равны 25 и 16. Ответ 200.
На стороне AB треугольника ABC как на диаметре построена окружность, пересекающая стороны AC и BC в точках D и E соответственно. Прямая DE делит площадь треугольника ABC пополам и образует с прямой AB угол 150. Найти углы треугольника ABC. Ответ: 450, 600, 750.
Через центр O окружности, описанной около треугольника ABC, проведены прямые перпендикулярно сторонам AC и BC. Эти прямые пересекают высоту CH или ее продолжение в точках P и Q. Найти радиус описанной окружности, если CP=p, CQ=q. Ответ:
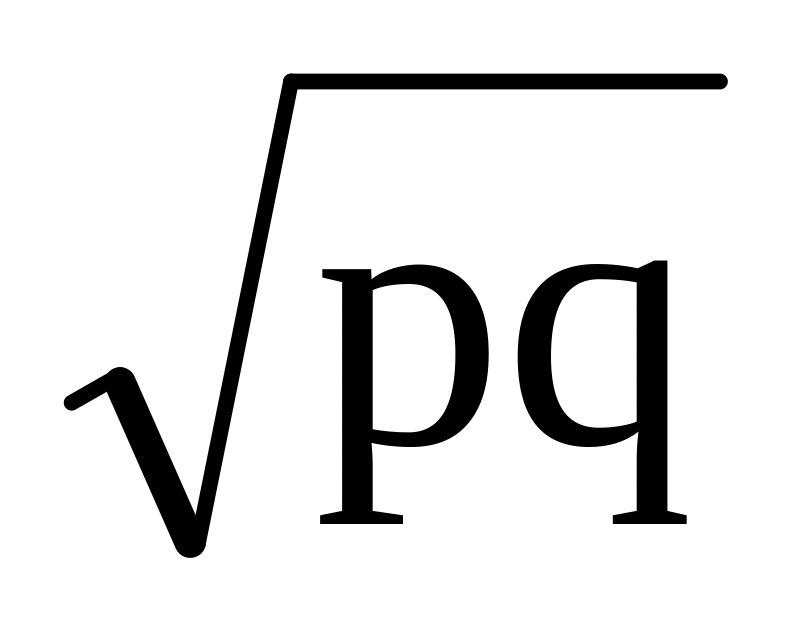 .
.В треугольнике АВС с периметром 2р острый угол ВАС равен α. Окружность с центром в точке О касается стороны ВС и продолжения сторон АВ и АС в точках К и L. Точка D лежит внутри отрезка АК и AD=а. Найти площадь треугольника DOK. Ответ:
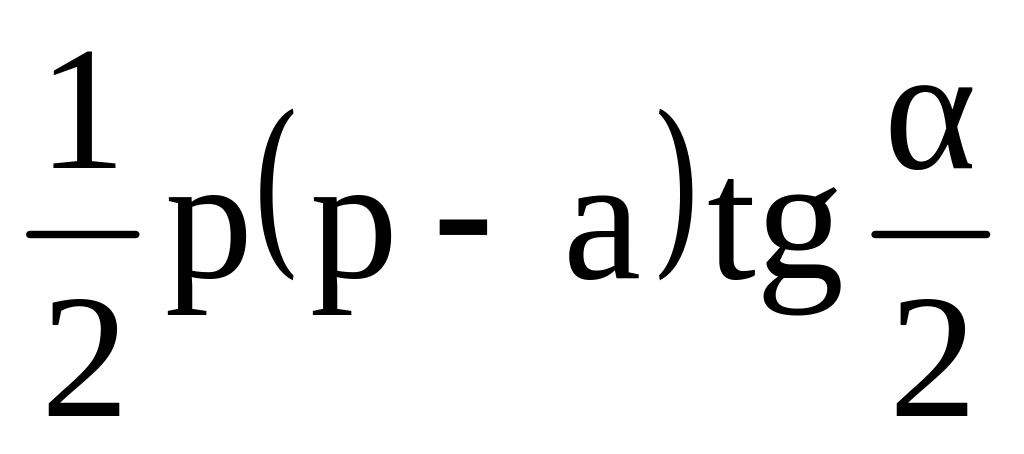 .
.К окружности, вписанной в треугольник с периметром 18, проведена касательная, параллельная основанию треугольника. Отрезок касательной, заключенный между боковыми сторонами треугольника, равен 2. Найти основание треугольника. Ответ: 3 или 6.
В треугольнике ABC с площадью 13 из центра O вписанной окружности на сторону AC опущен перпендикуляр OF. Найти FC, если AF=2, а радиус вписанной в треугольник AOF окружности равен
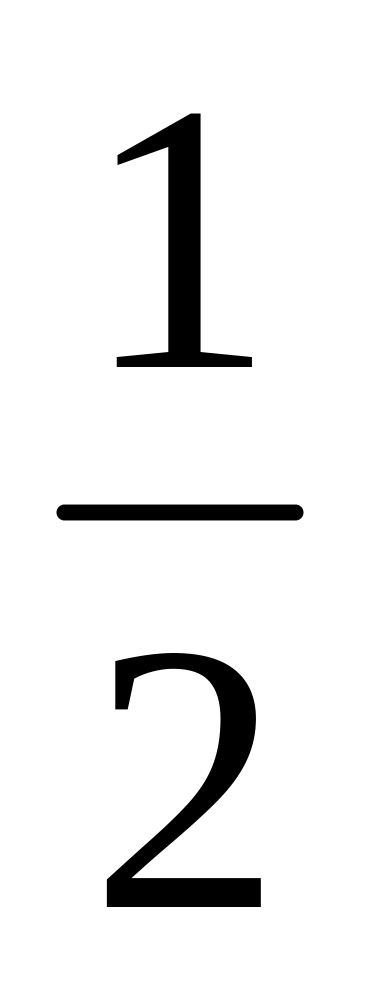 .
Ответ:
.
Ответ:
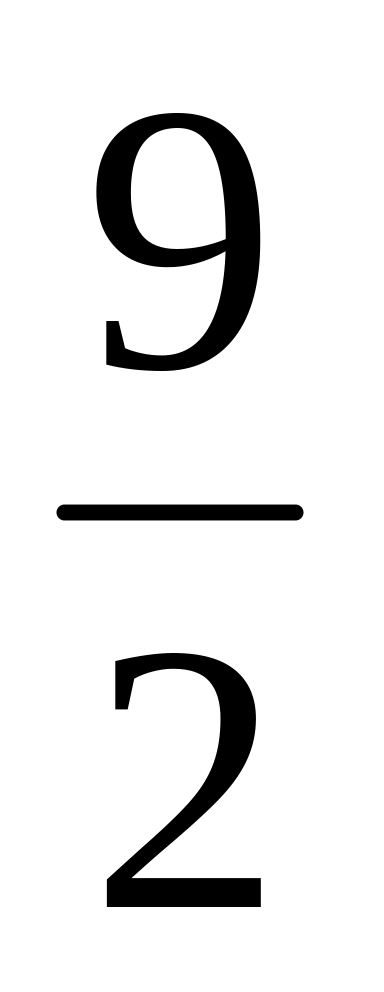 .
.
Дома:
Площадь треугольника равна 90, радиус описанной окружности равен
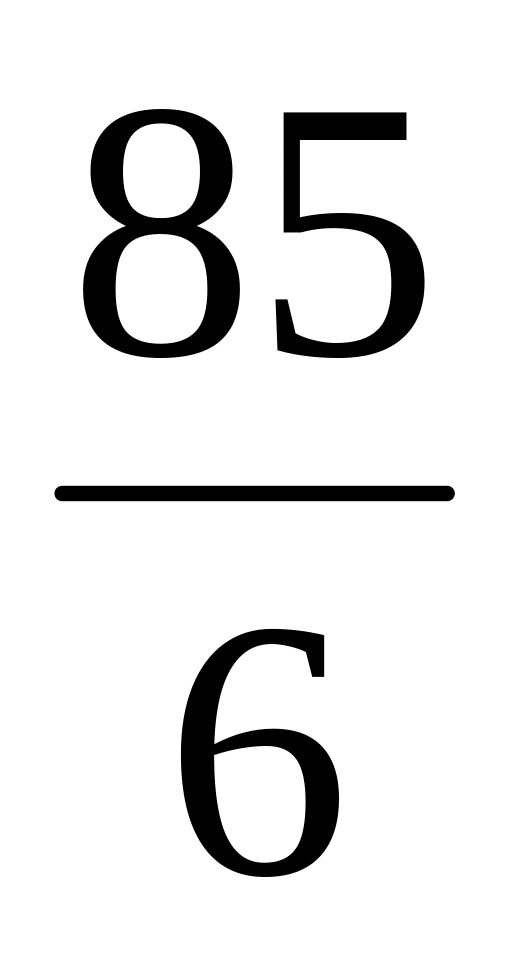 ,
а радиус вписанной окружности равен
,
а радиус вписанной окружности равен
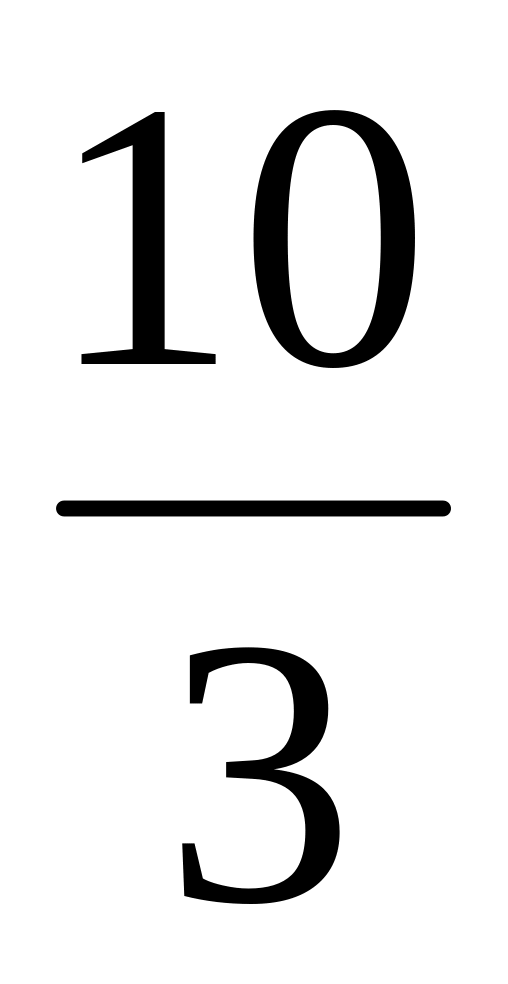 .
Найти длины сторон этого треугольника,
если одна из них равна 17. Ответ 12 и 25.
.
Найти длины сторон этого треугольника,
если одна из них равна 17. Ответ 12 и 25.В треугольнике PQR угол QRP равен 600. Найти расстояние между точками касания со стороной QR окружности радиуса 2, вписанной в треугольник, и окружности радиуса 3, касающейся продолжений сторон PQ и PR. Ответ: .
Окружность, построенная на стороне AC треугольника ABC как на диаметре, проходит через середину стороны BC и пересекает сторону AB в точке D, такой что AD:DB=1:2. Найти площадь треугольника ABC, если AC=1. Ответ:
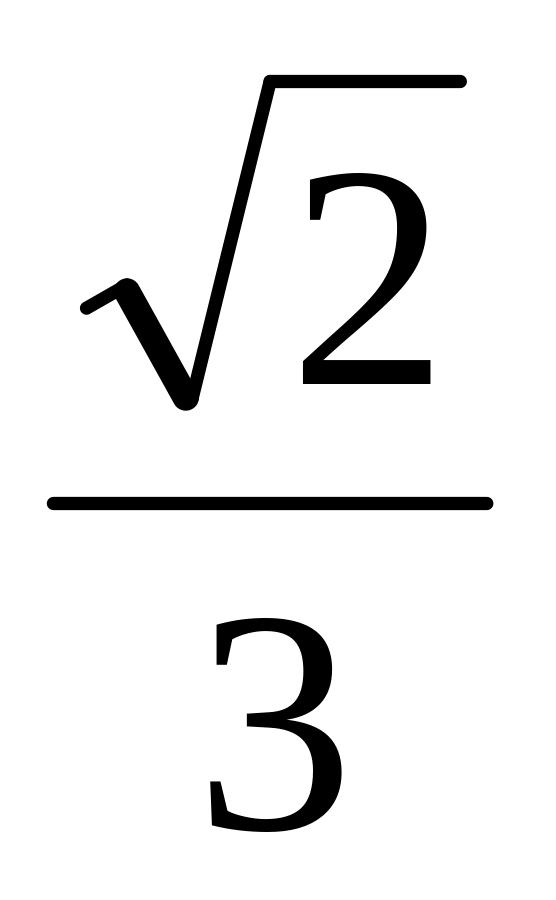 .
.В треугольнике АВС известно, что AC=b и АВС=α. Найти радиус окружности, проходящей через центр вписанного в треугольник АВС круга и вершины А и С. Ответ:
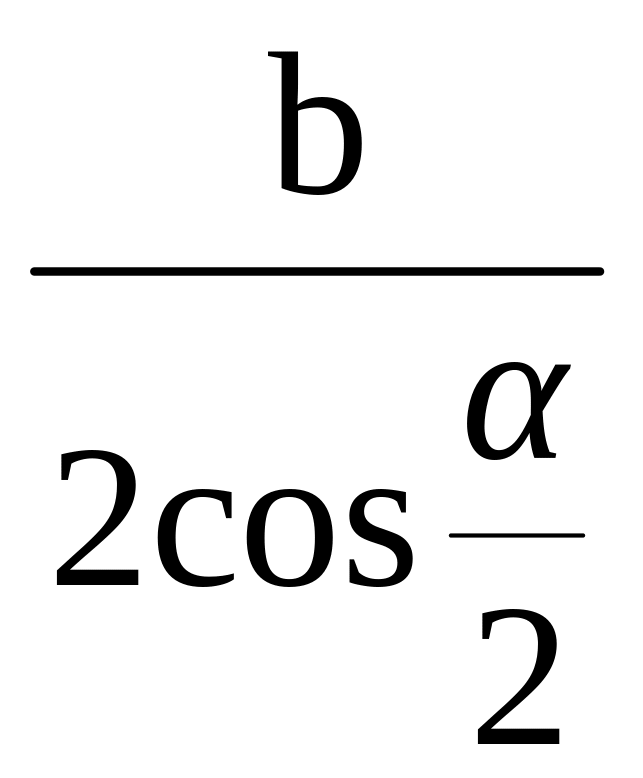 .
.Через вершины А и В треугольника АВС проходит окружность радиуса r, пересекающая сторону ВС в точке D. Найти радиус окружности, проходящей через точки А, С, D, если АВ=с и АС=b. Ответ:
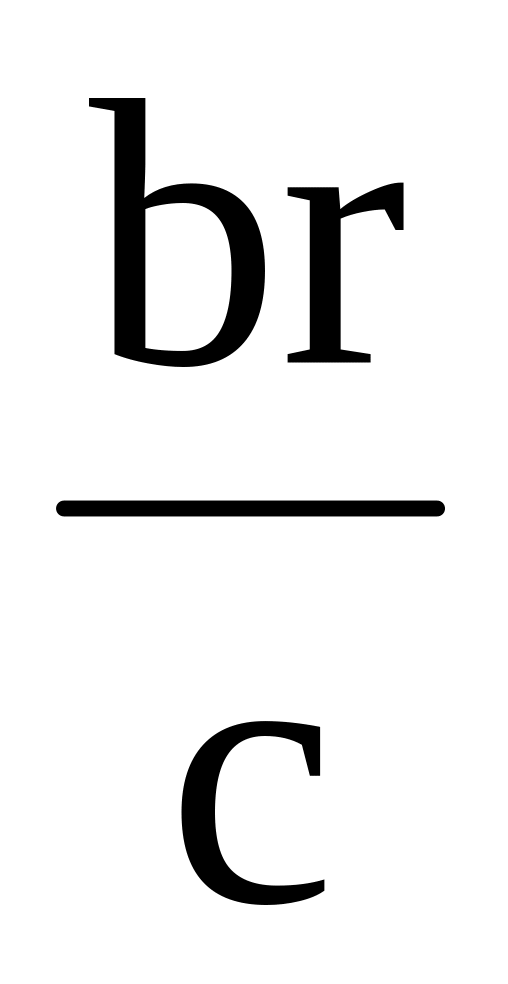 .
.Из вершины тупого угла A треугольника ABC опущена высота AD. Из точки D радиусом AD описана окружность, пересекающая стороны AB и AC в точках M и N соответственно. Найти AC, если AB=c, AM=m, AN=n. Ответ:
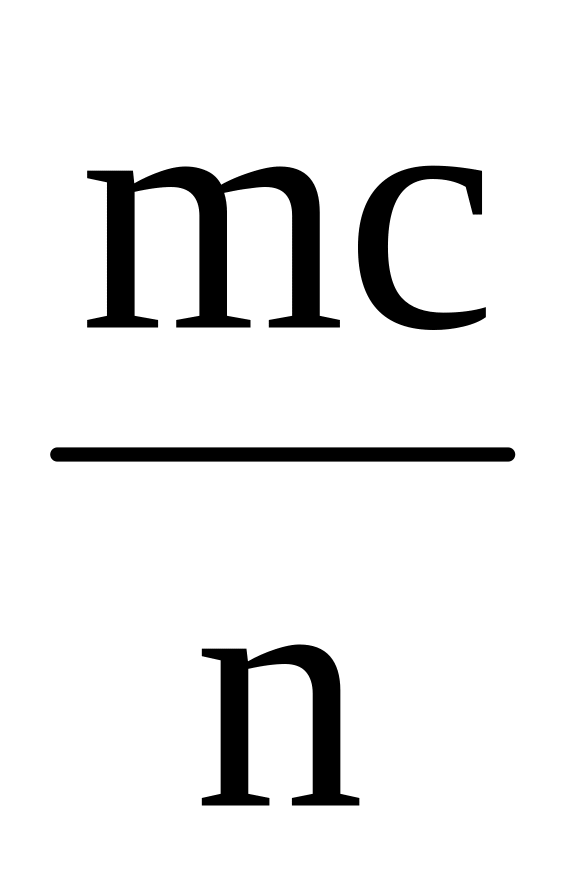 .
.В треугольнике АВС с периметром 2р сторона АС равна а, острый угол АВС равен α. Вписанная в треугольник АВС окружность с центром О касается стороны ВС в точке К. Найти площадь треугольника ВОК. Ответ:
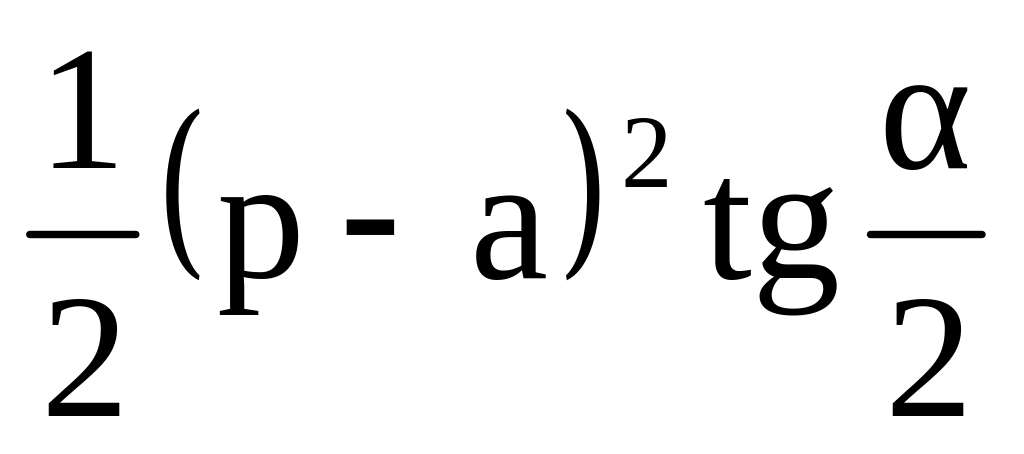 .
.В треугольник ABC со сторонами AB=4, AC=3 и BC=2 вписана окружность, касающаяся сторон AB и AC в точках M и N соответственно. Найти площадь треугольника AMN. Ответ:
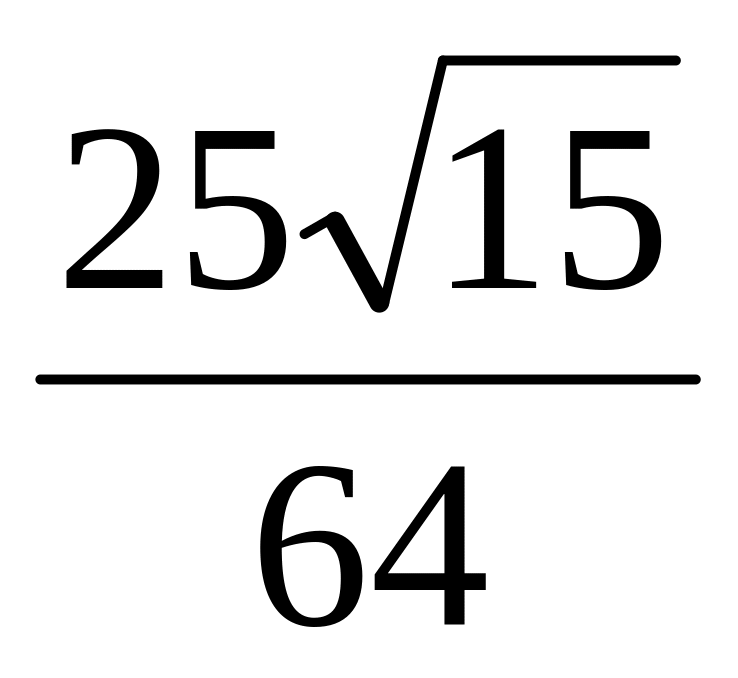 .
.В треугольнике АВС проведена медиана CD. Окружности, вписанные в треугольники ACD и BCD, касаются отрезка CD в точках М и N. Найти MN, если АС-ВС=2. Ответ: 1.
В треугольник вписана окружность радиуса 2. Одна из сторон треугольника делится точкой касания на отрезки 2 и 7. Найти радиус окружности, описанной около этого треугольника. Ответ: 5,3.
Окружность, вписанная в треугольник, точкой касания делит одну из сторон на отрезки 3 и 4, а противолежащий этой стороне угол равен 1200. Найти площадь треугольника. Ответ:
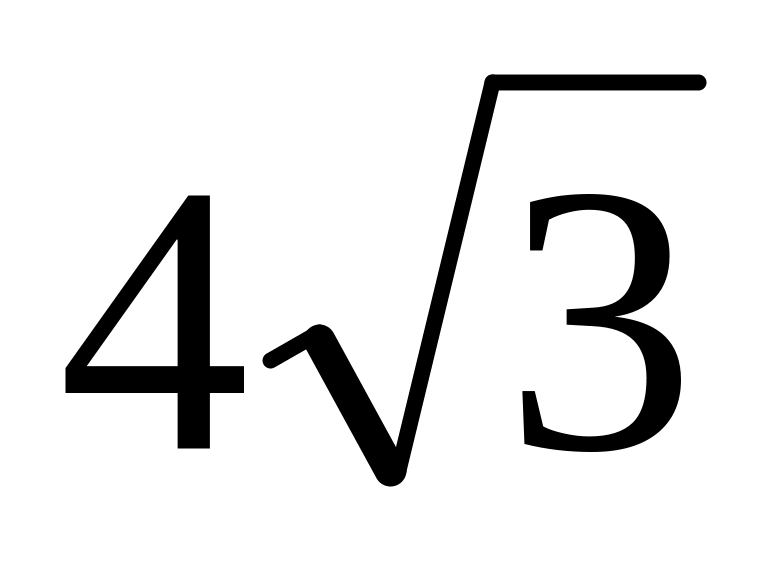 .
.Радиус вписанной в треугольник АВС окружности равен
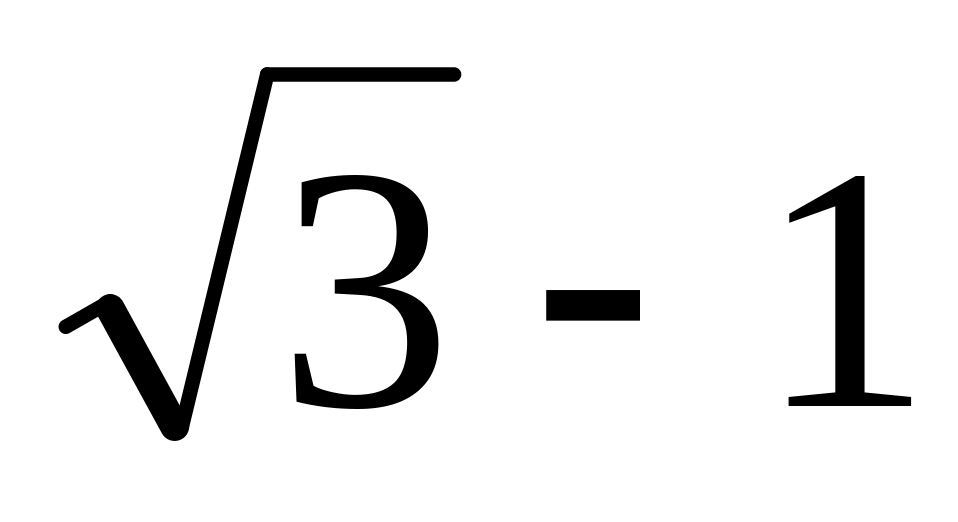 ,
угол ВАС равен 600, а радиус
окружности, касающейся стороны ВС и
продолжений сторон АВ и АС равен
,
угол ВАС равен 600, а радиус
окружности, касающейся стороны ВС и
продолжений сторон АВ и АС равен
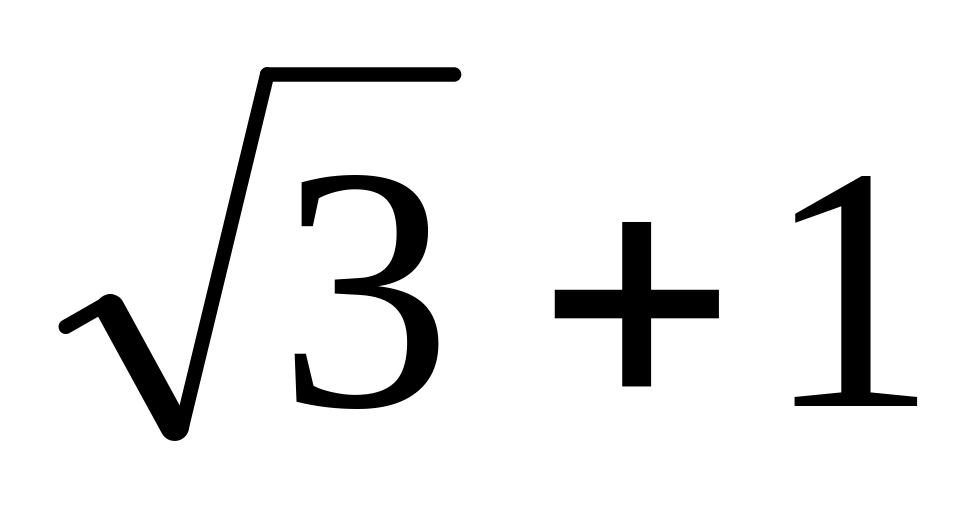 .
Найти углы АВС и АСВ. Ответ: 300 и 900.
.
Найти углы АВС и АСВ. Ответ: 300 и 900.
ЗАНЯТИЕ 5. Равнобедренный и равносторонний треугольник.
В классе:
Основание равнобедренного треугольника равно
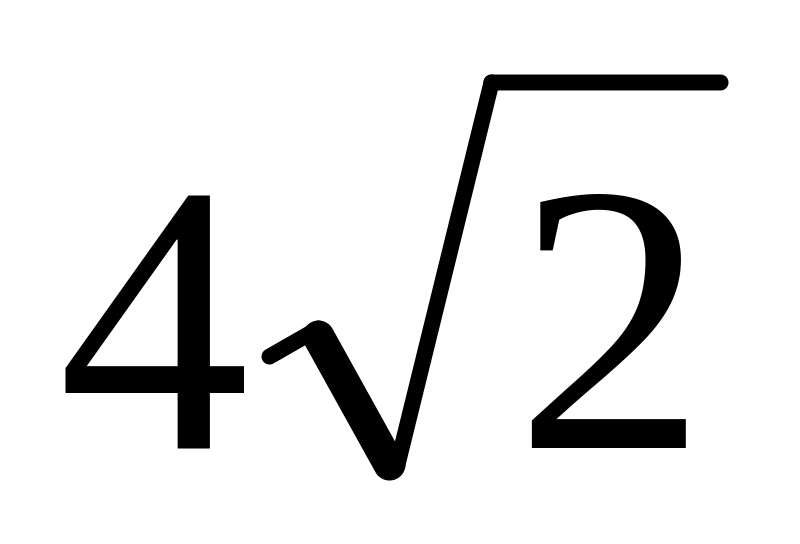 ,
а медиана его боковой стороны равна 5.
Найти боковую сторону этого треугольника.
Ответ: 6.
,
а медиана его боковой стороны равна 5.
Найти боковую сторону этого треугольника.
Ответ: 6.Биссектриса AD равнобедренного треугольника ABC с основанием AC делит его на два треугольника ABD и ACD, площади которых равны 4 и 2 соответственно. Найти стороны треугольника ABC. Ответ:
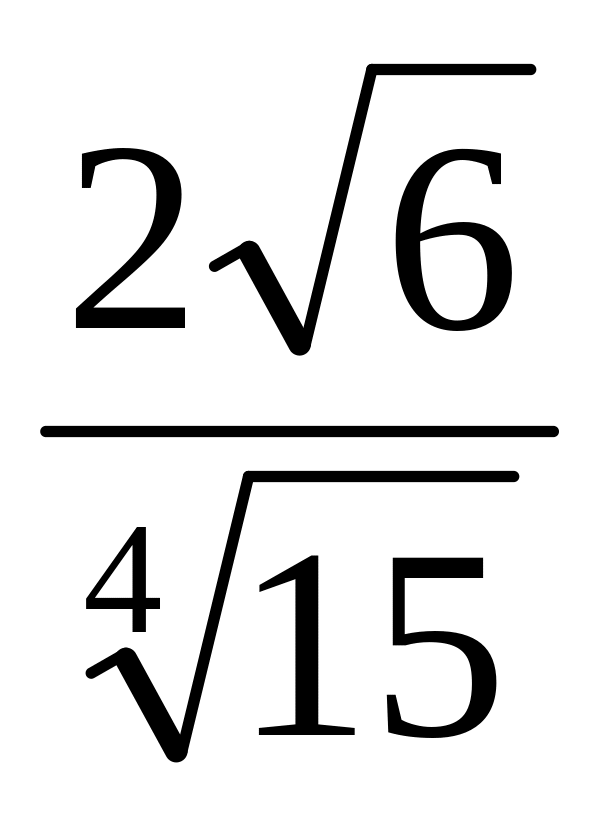 и
и
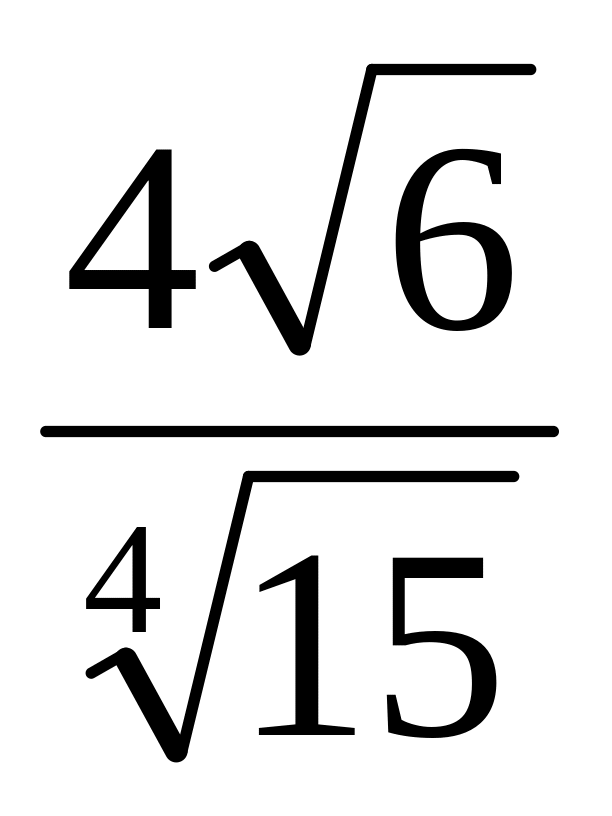 .
.Найти углы при вершине и основании равнобедренного треугольника, у которого точка пересечения высот делит пополам высоту, проведенную к основанию. Ответ:
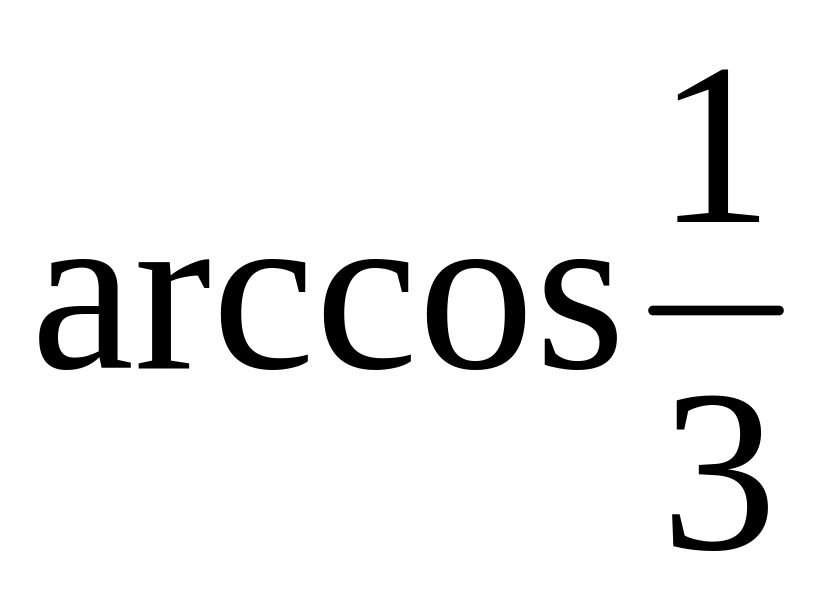 и
и
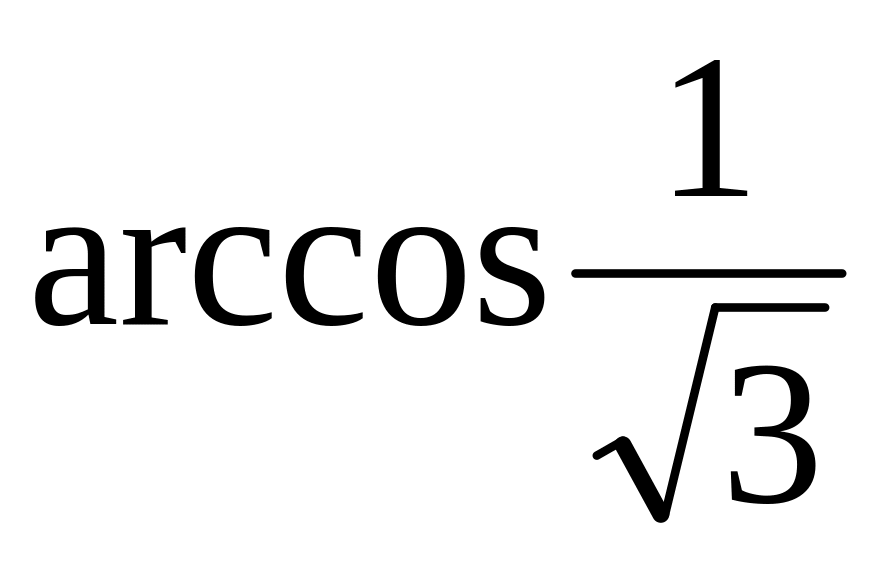 .
.На боковой стороне BC равнобедренного треугольника ABC как на диаметре построена окружность, пересекающая основание в точке D. Найти расстояние от вершины A до центра этой окружности, если AD= , ABC=1200. Ответ:
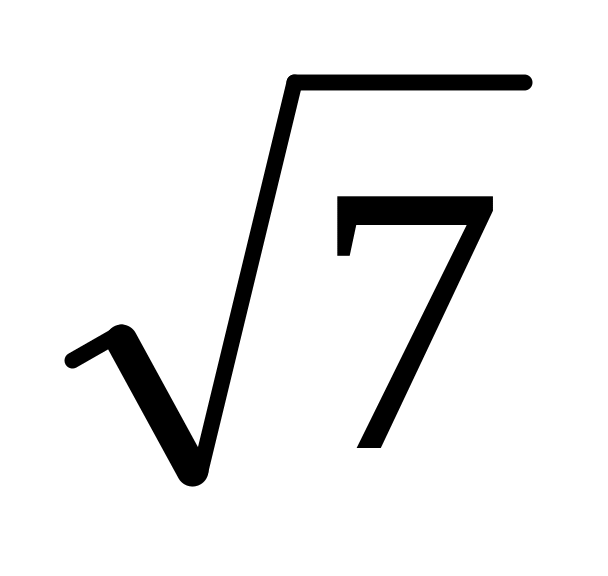 .
.В равнобедренный треугольник ABC с основанием AC вписана окружность радиуса 3, которая касается стороны BC в точке D. Найти AD, если BD=4. Ответ:
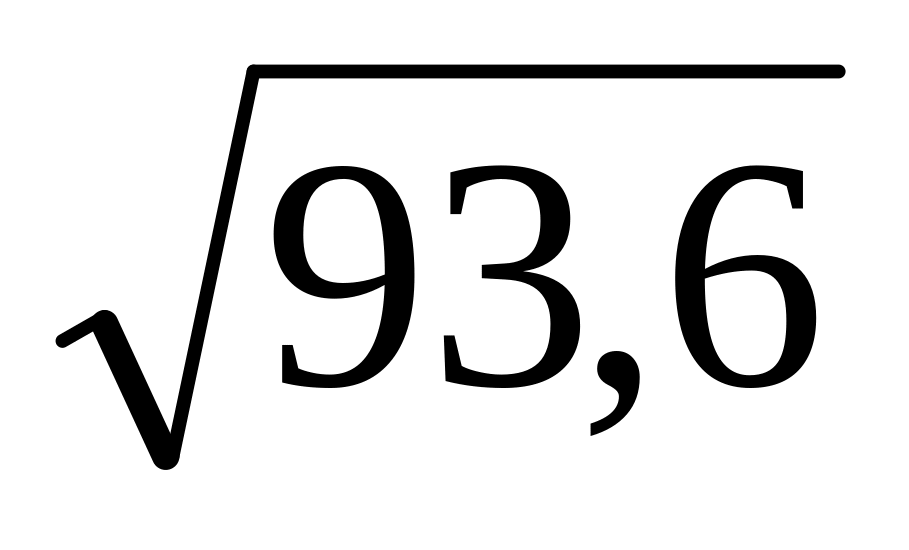 .
.Радиус окружности, описанной около равностороннего треугольника равен 1. Найти площадь этого треугольника. Ответ:
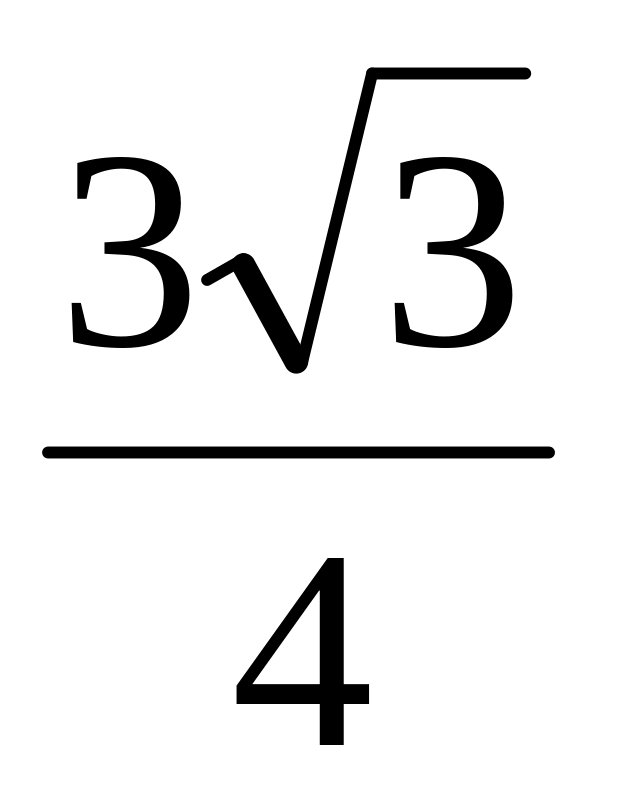 .
.
Дома:
Найти основание равнобедренного треугольника, если косинус угла при вершине равен
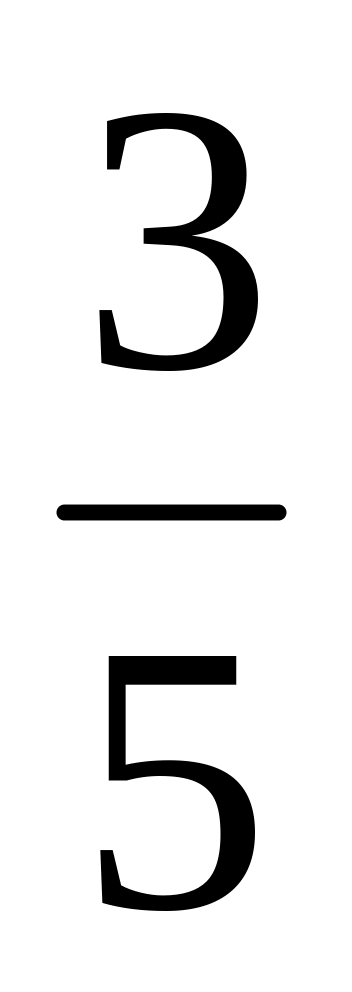 ,
а площадь равна 1. Ответ:
.
,
а площадь равна 1. Ответ:
.В равнобедренном треугольнике высота, опущенная на основание равна 5, а высота, опущенная на боковую сторону равна 6. Найти площадь этого треугольника. Ответ: 18,75.
На основании AC равнобедренного треугольника ABC как на диаметре построена окружность, пересекающая сторону BC в точке D. Найти площадь треугольника ABC, если BD:DC=3:2, AD=
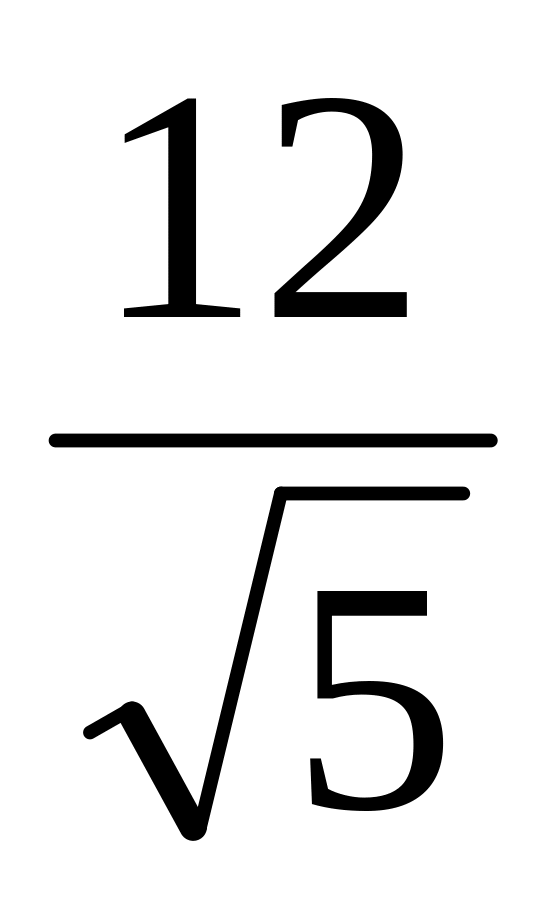 .
Ответ: 18.
.
Ответ: 18.Боковая сторона равнобедренного треугольника равна 10, а его основание равно 12. Найти расстояние между точками касания вписанной в этот треугольник окружности с его боковыми сторонами. Ответ: 4,8.
В равнобедренном треугольнике ABC с основанием AB центр O вписанной окружности делит высоту CD на отрезки CO=13 и OD=5. Найти длины сторон этого треугольника. Ответ: 15 и 19,5.
ЗАНЯТИЕ 6. Прямоугольный треугольник.
В классе:
В прямоугольном треугольнике ABC с прямым углом при вершине C выразить биссектрису, проведенную к катету BC через угол β при вершине B и гипотенузу AB=c. Ответ:
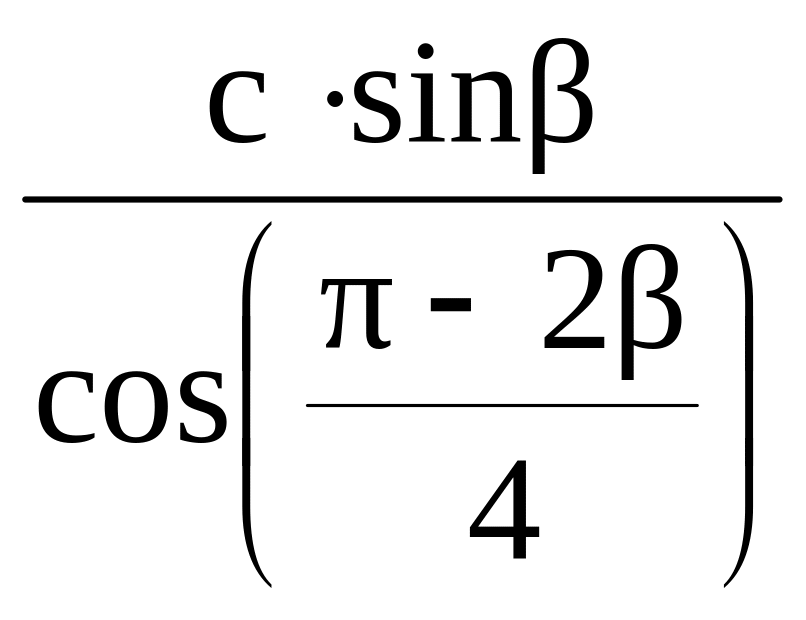 .
.Один из катетов прямоугольного треугольника равен 15, а проекция другого катета на гипотенузу равна 16. Найти радиус вписанной в этот треугольник окружности. Ответ: 5.
В прямоугольный треугольник с периметром 36 вписана окружность. Гипотенуза делится точкой касания в отношении 2:3. Найти гипотенузу. Ответ: 15.
В прямоугольном треугольнике отношение высоты к медиане, проведенным из вершины прямого угла равно 4:5. Найти острые углы этого треугольника. Ответ:
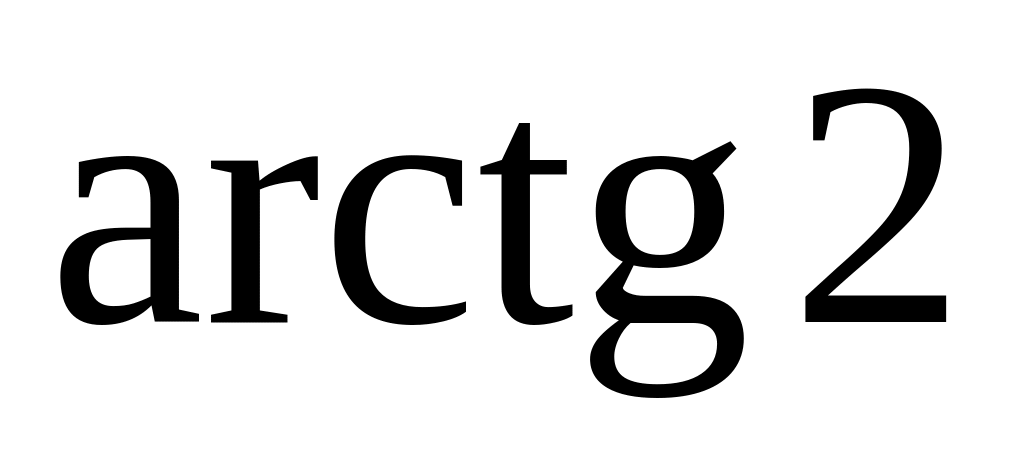 и
и
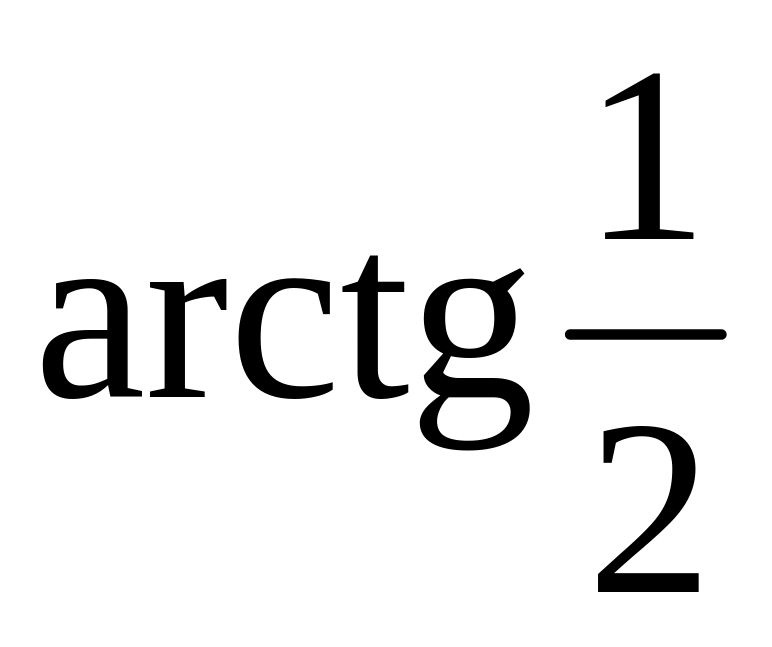 .
.В прямоугольном треугольнике АВС катеты АВ и АС равны 4 и 3 соответственно. Точка D делит гипотенузу ВС пополам. Найти расстояние между центрами окружностей, вписанных в треугольники ADC и ABD. Ответ:
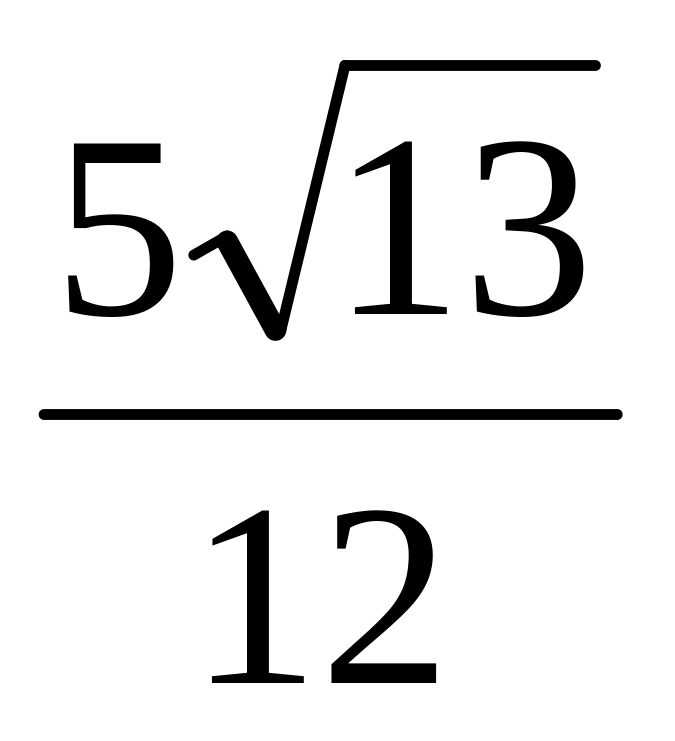 .
.Гипотенуза АВ прямоугольного треугольника АВС является хордой окружности радиуса 10. Вершина С лежит на диаметре этой окружности, параллельном гипотенузе. Угол САВ равен 750. Найти площадь треугольника АВС. Ответ: 40.
Прямоугольный треугольник с периметром 10 разбит высотой, опущенной на гипотенузу, на два прямоугольных треугольника. Периметр одного из них равен 6. Найти периметр другого. Ответ: 8.
Дома:
В прямоугольном треугольнике ABC с прямым углом при вершине C выразить катет BC через угол α при вершине A и медиану AM=m, проведенную к катету AC. Ответ:
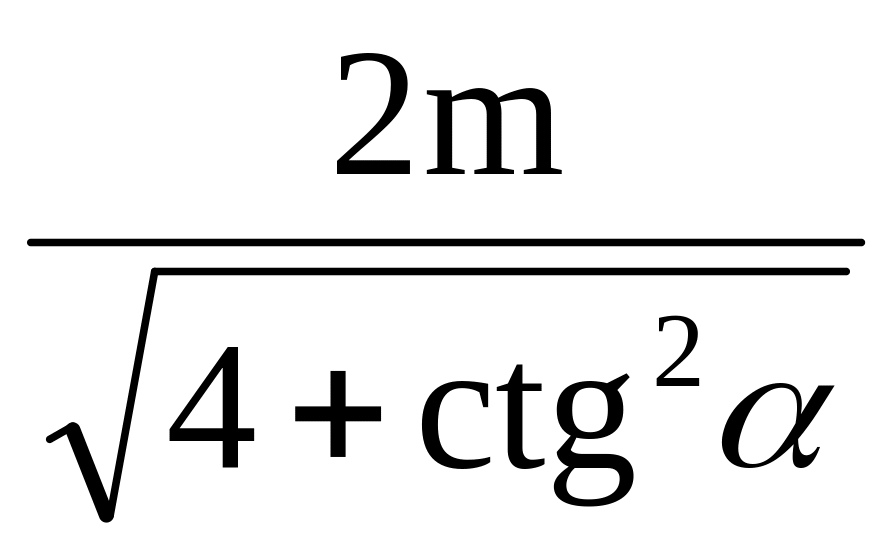 .
.В прямоугольном треугольнике высота, опущенная из вершины прямого угла, делит гипотенузу на отрезки 9 и 16. Найти радиус вписанной в этот треугольник окружности. Ответ: 5.
В прямоугольном треугольнике катета относятся как 2:3, а высота делит гипотенузу на отрезки, разность длин которых равна 2. Найти гипотенузу этого треугольника. Ответ: 5,2.
В прямоугольном треугольнике медианы острых углов равны
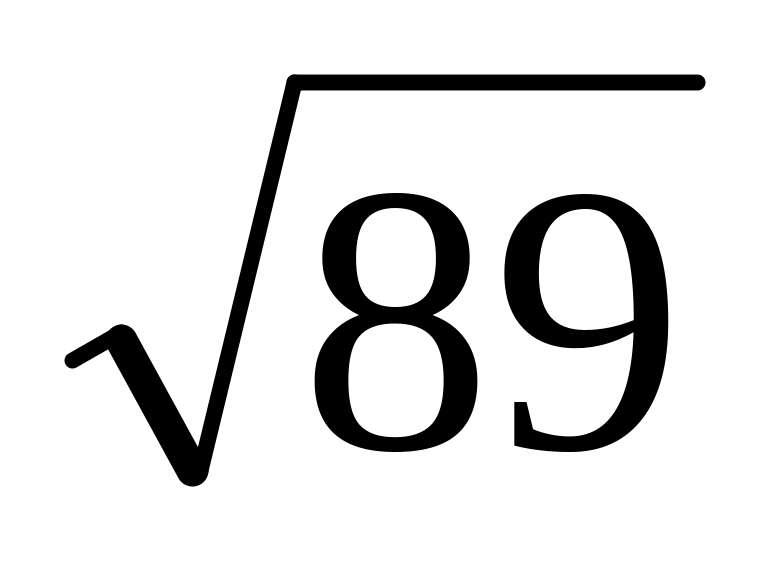 и
и
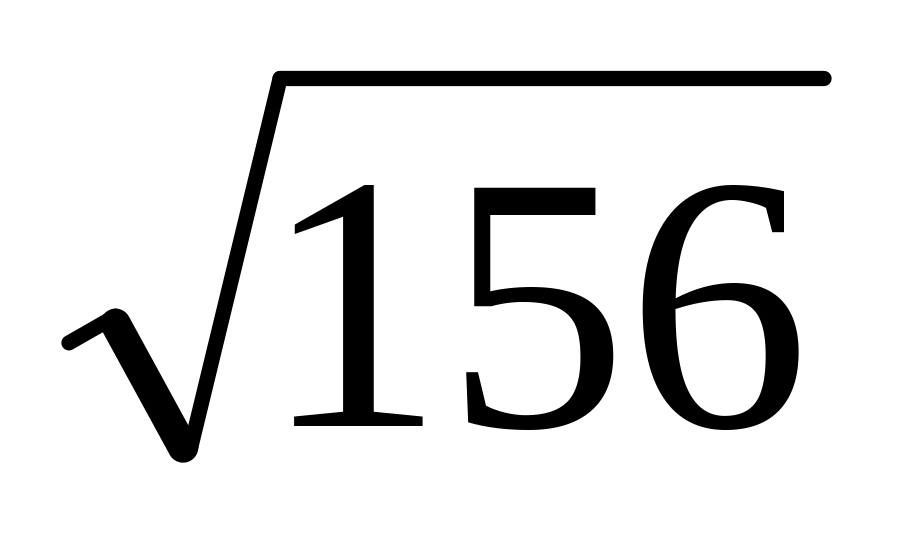 .
Найти гипотенузу этого треугольника.
Ответ: 14.
.
Найти гипотенузу этого треугольника.
Ответ: 14.В прямоугольном треугольнике биссектриса прямого угла делит гипотенузу на отрезки 3 и 4. Найти площадь этого треугольника. Ответ: 11,76.
Точка пересечения медиан прямоугольного треугольника удалена от его катетов на расстояния 3 и 4. Найти расстояние от этой точки до гипотенузы. Ответ: 2,4.
Катет прямоугольного треугольника равен 2, а противолежащий ему угол равен 300. Найти расстояние между центрами окружностей, вписанных в треугольники, на которые данный треугольник разбит медианой, проведенной из вершины прямого угла. Ответ:
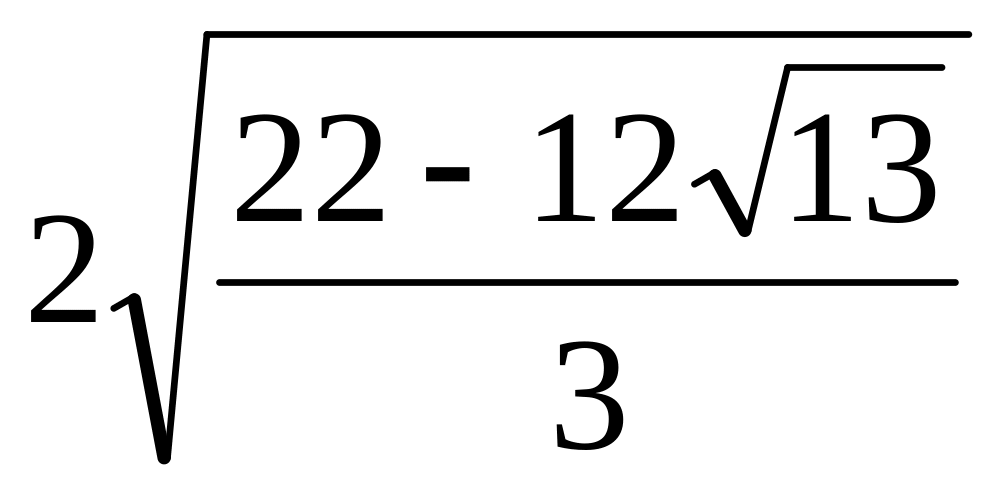 .
.Гипотенуза КМ прямоугольного треугольника КМР является хордой окружности радиуса . Вершина Р находится на диаметре, параллельном гипотенузе. Расстояние от центра от центра окружности до гипотенузы равно . Найти острые углы треугольника КМР. Ответ: 300, 600.
Окружность, центр которой лежит на гипотенузе AB прямоугольного треугольника ABC, касается катетов AC и BC в точках E и D соответственно. Найти угол при вершине B, если AE=1, BD=3. Ответ: 300.
