Числа Каталана

Перейдем к описанию производящей функции S(t) для ряда C(n) из чисел Каталана. В некотором смысле нахождение этой производящей функции будет даже проще, чем нахождение производящей функции для чисел Фибоначчи. Попробуем записать формулу (1) для генератрисы S(t). Здесь нам придется умножать ее саму на себя. Действительно, коэффициент при n–й степени переменной t в ряде равен сумме произведений коэффициентов при степенях j,k ряда S(t) при j+k=n, т.е. C(0)C(n)+C(1)C(n-1)+…+C(n)C(0). Это в точности формула для C(n+1). Таким образом, нам нужно возвести S(t) в квадрат, сдвинуть не единицу (т.е. умножить на t) и добавить на нулевое место коэффициент 1. Тогда мы и получим S(t). Более строго:

.

Посмотрим теперь на S(t) как на обычную функцию от переменной t и для ее нахождения решим квадратное уравнение:

(3)

В отличие от чисел Фибоначчи, в данное квадратное уравнение рассматривается уже не как уравнение относительно переменной t, а как уравнение относительно производящей функции S(t).

Решая это уравнение, мы получим формулу . Но как ее понимать? Мы ведь должны получить ряд, а получаем квадратный корень, да еще t в знаменателе. Научимся сначала трактовать квадратный корень. Квадратный корень — это половинная степень числа. Попробуем выразить эту степень по биному Ньютона. При этом надо понимать, какое число должно играть роль “числа сочетаний из по k” . Поступим формальным образом. Для этого просто запишем формулу для получения числа сочетаний также как и в случае целых чисел:

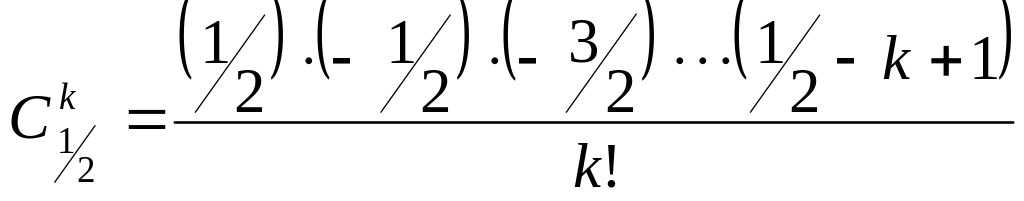(4)

Замечание. Сейчас мы просто пытаемся провести аналогии со случаем целых чисел, что дает нам эвристический подход к вычислению чисел Каталана. В дальнейшем, получив результат, нам останется лишь убедиться в том, что он верен.

Заметим, что в отличие от целого числа n, для которого при k>n , для числа никогда не обращаются в нуль, так как числитель формулы (4) содержит лишь полуцелые числа. Это значит, что для разложения корня по “биному Ньютона” нам потребуется не конечная сумма слагаемых, а бесконечный ряд. Таким образом, мы получим:

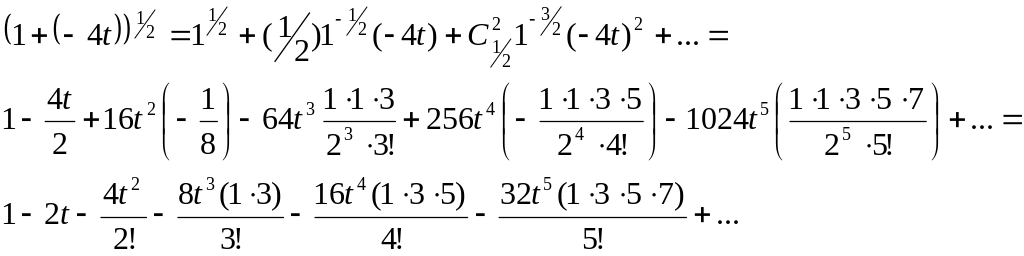(5)

Теперь получившееся в (5) выражение нужно прибавить к единице (или вычесть из единицы) и разделить на 2t для получения производящей функции для чисел Каталана.

Так как все члены формулы (5), кроме свободного, стоят со знаком минус, а числа Каталана положительные, понятно, что этот ряд из единицы нужно вычитать.

Следовательно, мы получаем

Коэффициент, стоящий при , и есть n–е число Каталана. Попытаемся упростить его.

Имеем:

(6)

Итак, мы получили явную (не рекуррентную) формулу для вычисления чисел Каталана. В том, что эта формула действительно описывает числа Каталана, мы убедимся чуть позже.

Если эту формулу принять на веру, то мы получим, что число нацело делится на (n+1) — факт далеко не очевидный.

Числа Каталана и теория вероятностей

Билеты в театр и хождение по треугольнику Паскаля

Хорошо известно правило, по которому строятся числа в треугольнике Паскаля.

Его нулевая строка содержит один член, равный единице. Далее, в первой строке стоят два числа, оба равные единице, происходящие от единице в нулевой строке, одно — справа от элемента нулевиой строки, другое — слева.. Вторая строка состоит из трех чисел: крайние (нулевое и второе) — единицы, а среднее — двойка, представляющая собой сумму двух единиц из первой строки. Средний элемент второй строки стоит в точности под элементом нулевой строки. В третьей строке уже четыре числа, крайние (нулевое и третье) равны единицы, а средние (первое и второе) — тройке. Каждая следующая строка содержит на один элемент больше чем предыдущая, при этом каждый элемент следующей строки равен сумме двух ближайших к нему элементов предыдущей строки: сверху слева и сверху справа. Элементы треугольника Паскаля имеют важную комбинаторную интерпретацию: элемент из n–й строки и k–го столбца обозначается через и равен числу возможных выборов k различных неупорядоченных элементов из числа n данных. Проверка этого факта оставляется читателю в качестве приятного и полезного упражнения.

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

1 7 21 35 35 21 7 1

………..……………

Треугольник Паскаля

Так, например, число 21— второе в седьмой строке, если не считать начального (нулевого) числа 1— равно сумме первого и второго чисел в шестой строке.

Рассмотрим начальную вершину треугольника Паскаля, в которой стоит число 1, и будем бросать монету. При выпадении орла будем двигаться вниз и направо, а при выпадении решетки — вниз и налево. После n бросаний мы попадем в n–ю строку треугольника Паскаля на какое–то место. На этом месте будет стоять число, равное всевозможному количеству различных последовательностей исходов бросания монетки, при котором мы попадаем на это место. Так как на каждое место мы можем попасть либо сверху справа, либо сверху слева, то и соответствующее число будет равно сумме чисел, над ним стоящих. При этом, так как всего различных исходов бросания монетки существует , то этому же числу будет равна сумма всех чисел в n–й строке треугольника Паскаля.

Вернемся теперь к нашей задаче о числах Каталана и билетах в театр. Каждому человеку, стоящему в очереди, можно сопоставить результат бросания монетки следующим образом. Если у него в наличии пятирублевая купюра, то это соответствует выпадению орла, а если десятирублевая — выпадению решетки. Таким образом, произвольная очередь в театр, состоящая из людей с пяти– и десятирублевыми купюрами, также соответствует хождению по треугольнику Паскаля. При этом мы помним, что в задаче у нас было ограничение: в кассе всегда должно хватать пятирублевых банкнот. Это означает, что при нашем хождении мы не должны заходить левее начальной точки. Таким образом, нам нужно построить “урезанный” треугольник Паскаля — соответствующий хождению только по правой стороне. Вот как он будет выглядеть:

1

1

1 1

2 1

2 3 1

5 4 1

5 9 5 1

14 14 6 1

14 28 20 7 1

42 48 27 8 1

42 90 75 35 9 1

132 165 110 44 10 1

132 297 275 154 54 11 1

Как мы видим и как должно быть на самом деле, в столбце, расположенном под начальной точкой, как раз расположились числа Каталана — количества всевозможных “правильных” очередей в театр или правильных хождений по (урезанному) треугольнику Паскаля. Попытаемся отыскать общую закономерность построения такого треугольника.