
- •Числа Каталана
- •Три задачи о числах Каталана
- •Рекуррентная формула для чисел Каталана.
- •Производящие функции
- •Числа Фибоначчи, золотое сечение и цепные дроби Явная формула для чисел Фибоначчи
- •Золотое сечение
- •Цепные дроби
- •Числа Каталана
- •Билеты в театр и хождение по треугольнику Паскаля
- •Принцип отражения в теории вероятностей
- •Принцип отражения и числа Каталана
- •Распределение времени выигрыша
Числа Каталана
Многим наверняка знакома последовательность натуральных чисел 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,… в которой каждое следующее число является суммой двух предыдущих. Эти числа носят имя знаменитого средневекового итальянского математика Фибоначчи, также известного как Леонардо Пизанский. У этих чисел есть много замечательных свойств, о которых мы расскажем в настоящей статье.
Существуют и другие замечательные последовательности натуральных чисел, об одной из которых мы расскажем в настоящей статье. Эта последовательность начинается числами 1, 2, 5, 14, 42,132, …; ее члены называются числами Каталана в честь бельгийского математика Эжена Шарля Каталана. Эти числа связаны с различными задачами комбинаторики, теории вероятностей, теории чисел. О закономерности построения следующего члена последовательности по предыдущим ее членам мы поговорим чуть позже, а пока рассмотрим некоторые задачи, в которых эти числа появляются. Более углубленно о комбинаторике таких последовательностей чисел можно прочесть в [1].
Три задачи о числах Каталана
Будем рассматривать расстановки круглых скобок. Назовем расстановку скобок правильной, если все скобки разбиты на пары, причем каждая пара состоит из открывающей и закрывающей скобок, причем закрывающая скобка расположена позднее соответствующей ей открывающей, а для любой скобки b, лежащей между открывающей скобкой a и парной ей закрывающей скобкой a’ парная скобка b’ также лежит между a и a’.
Задача 1. Сколько существует правильных расстановок n пар скобок для фиксированного натурального числа n ?
Пример. Расстановка скобок ( ( ) ( ) ) ( ) является правильной, а ( ) ) ( — неправильной, т.к. скобки, выделенные красным цветом не являются парными, у каждой из них нет пары.
Для небольших значений переменной n нетрудно посчитать ответ путем перебора: для одной пары существует одна расстановка скобок: ( ), для двух — две: ( ) ( ) и ( ( ) ), для трех — пять: ( ) ( ) ( ), ( ) ( ( ) ), ( ( ) ) ( ), ( ( ) ( ) ), ( ( ( ) ) ).
Перейдем теперь к другим задачам, на первый взгляд не похожим на первую.
Задача 2. Сколькими способами можно разбить выпуклый (n+2)–угольник на треугольники непересекающимися диагоналями?
Для этой задачи также нетрудно посчитать ответ для малых n: для треугольника (n=1) такой способ один, для четырехугольника (n=2) — два (можно выбрать любую из двух диагоналей, и она будет разбивать четырехугольник на два треугольника), для пятиугольника (n=3) — пять, для шестиугольника (n=4) — четырнадцать Все эти разбиения показаны на рис. 1.
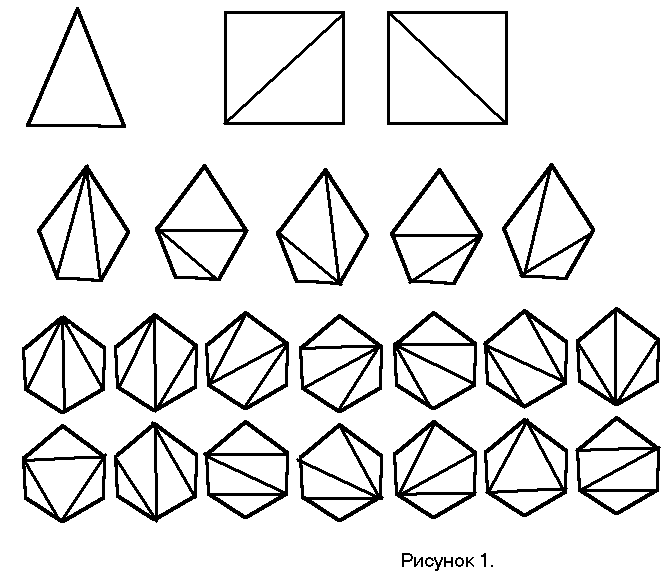

Задача 3. У театральной кассы стоит очередь за билетами из 2n человек. Билет стоит пять рублей, а в наличии у каждого из стоящих в очереди есть ровно одна банкнота — либо пять, либо десять рублей, причем каждый из двух видов банкнот встречается ровно у n человек. У кассира в начальный момент нет пятирублевых банкнот. Каждый, стоящий в очереди, покупая билет, если дает десятирублевую банкноту, должен получить сдачу. Какова вероятность того, что на протяжении всей очереди у кассира всегда будет достаточный запас пятирублевых банкнот для сдачи, а в конце у него не останется пятирублевых купюр?
Легко
видеть, что всего существует
![]() возможных
ситуаций (ровно столько есть способов
распределить среди 2n
любителей театра n
человек, у которых на руках десятирублевая
купюра и n
человек с пятирублевыми купюрами на
руках). Следовательно, для решения задачи
нужно посчитать, в скольких случаях у
кассира на протяжении всей очереди
будут иметься в достаточном количестве
пятирублевые купюры, причем в последний
момент они у него закончатся. Полученное
число случаев нужно разделить число
случаев на
.
возможных
ситуаций (ровно столько есть способов
распределить среди 2n
любителей театра n
человек, у которых на руках десятирублевая
купюра и n
человек с пятирублевыми купюрами на
руках). Следовательно, для решения задачи
нужно посчитать, в скольких случаях у
кассира на протяжении всей очереди
будут иметься в достаточном количестве
пятирублевые купюры, причем в последний
момент они у него закончатся. Полученное
число случаев нужно разделить число
случаев на
.
Подсчет таких случаев для малых значений числа n опять приводит нас к знакомой последовательности: при n=1 это число равно единице, при n=2 — двум, далее пяти, четырнадцати, и т.д.
По ответам видно, что для этих задач прослеживается некоторая закономерность, которая связана с числами Каталана. При этом мы до сих пор не выяснили, по каким правилам вычисляются члены этой знаменитой последовательности.
