2. Будь-які дві твірні однієї сім'ї не перетинаються і не паралельні, тобто є мимобіжними.

Доведення. Дійсно, ці прямі не можуть перетинатися, бо інакше через точку їх перетину проходило б дві твірні однієї сім'ї, що супе­речить властивості 1.

Ці прямі не можуть бути і паралельними. Щоб переконатися в цьому, покажемо, що напрямні вектори прямих (32) при різних зна­ченнях параметра Х₁ і λ₂ (λ_г і λ₂) неколінеарні.

Знайдемо координати напрямного вектора прямої (32). Пере­пишемо систему (32) у вигляді:

Напрямним вектором даної прямої є

Напрямні вектори двох прямих із цієї сім'ї, що відповідають па­раметрам λ₁ і λ₂, такі:

Перевіримо, чи можуть бути вони колінеарними. Прирівнявши відношення відповідних координат, матимемо:

Звідки:

Ця система сумісна, якщо λ₁ = λ₂. Отже, || р₂ тоді і тільки тоді, коли λ₁ = λ₂. Якщо ж λ₁ ≠ λ₂ то || р₂ .Це і доводить, що прямі не

паралельні. Отже, вони мимобіжні. Аналогічно розглядаються і пря­молінійні твірні другої сім'ї (33).

3. Довільні дві твірні різних сімей перетинаються або паралельні.

Доведення. Розглянемо дві довільні твірні з різних сімей, при цьому нехай твірній із першої сім'ї відповідає параметр λ₁, а з другої - λ₂. Щоб з'ясувати питання про перетин цих прямих, необхідно досліди­ти систему рівнянь

О скільки одне з рівнянь системи є наслідком трьох інших (на­приклад, 4-те рівняння утворюється внаслідок почленного множення перших двох і ділення на відповідні частини третього рівняння), то І дослідимо систему з трьох перших рівнянь:

або

Визначник цієї системи

Якщо λ₁ ≠ λ₂, то Δ≠0, Таким чином, система має єдиний розв'язок, а отже, прямі перетинаються.

Якщо λ₁ = -λ₂, то Δ=0, а самі прямі паралельні.

Зауважимо, що, крім названих сімей прямолінійних твірних (32) і (33), є ще чотири прямі, які лежать у площинах, паралельних до координатної площини OXZ, і повністю належать однопорожнинному гіперболоїду. Це такі прямі:

Вони разом із сім'ями (32) і (33)визначають усі рямі, що повністю лежать на однопорожнинному гіперболоїді.

Таким чином, однопорожнинний гіперболоїд є лінійчатою повер­хнею (рис.30). Ця властивість широко використовується в будіве­льній техніці. Відомий російський інженер Володимир Григорович Шухов запропонував конструкцію з металевих балок, розміщених так, як прямолінійні твірні однопорожнинного гіперболоїда обертання. Ці конструкції виявилися дуже міцними і легкими. Вони часто ви­користовуються при будівництві водонапірних башт, високих радіо-і телещогл.

Прямолінійні твірні гіперболічного параболоїда

Розглянемо гіперболічний параболоїд, заданий канонічним рівнянням

(27)

Перетворимо це рівняння так:

Розглянемо дві системи рівнянь:

і

Ці системи визначають рівняння прямих, які повністю лежать на гіперболічному параболоїді, бо якщо перемножити відповідні части­ни рівнянь однієї системи, то одержимо рівняння (27) при довіль­ному Я, відмінному від нуля.

Аналогічно, як і для однопорожнинного гіперболоїда, крім запи­саних, є ще дві прямі, які також повністю належать гіперболічному параболоїду. Це такі прям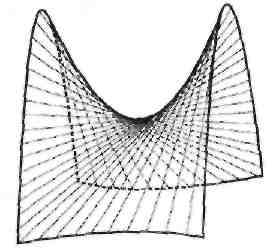і:

і

Всі ці прямі називаються прямолінійними твірни­ми гіперболічного параболоїда. Вони мають такі ж вла­стивості, як і прямолінійні твірні однопорожнинно­го гіперболоїда:

1. Рис. 31

   Через довільну точку гіперболічного параболоїда проходить одна і тільки одна твірна з кожної сім'ї.

2. Будь-які дві твірні однієї сім'ї є мимобіжними.

3. Будь-які дві твірні різних сімей перетинаються або паралельні.

Пропонуємо довести ці властивості самостійно. Таким чином, гіперболічний параболоїд також є лі­нійчатою поверхнею (рис. 31).

М ожна показати, що однопорожнинний гіперболо­їд утворюється рухом прямої, яка ковзає по трьох мимобіжних прямих. Аналогічно гіперболічний параболоїд можна утворити рухом прямої, яка ковзає по двох мимобіжних прямих і залишається при ньому весь час паралельною заданій площині. Природно виникає запитання: чи мають прямолінійні твірні такі поверхні другого порядку, як еліпсоїд, двопорожнинний гіперболоїд і еліптичний параболоїд? Відповідь проста: ні. Покажемо це на прикладі еліпсоїда. Як було встановлено, еліпсоїд лежить всередині деякого прямокутного паралелепіпеда, тобто є обмеженою поверхнею. Але кожна пряма є необмеженою лінією, а тому не може повністю лежати на еліпсоїді. Приклад. На гіперболічному параболоїді знайти прямолінійні твірні, паралельні до площини 3x+2y-4z. Розв'язання. Запишемо рівняння двох сімей прямолінійних твірних даного гіперболічного параболоїда:

(36)

(37)

Знайдемо координати напрямних векторів прямих із сім'ї (36):

Координати напрямних векторів прямих (37):

Вектор паралельний до площини 3х + 2у — 4z = 0,

якщо 2 • 3 + 1 • 2 + λ• (-4) - 0, звідки λ = 2. Тоді прямою із сім'ї (36), паралельною до даної площини, є пряма

з напрямним вектором

Точка М1(4; -2; 0) належить цій прямій. Тому її канонічне рівняння

Вектор паралельний до даної площини, якщо 2 • 3 -1 • 2+λ · (-4)=0, звідки λ= 1. Тому . Рівняння другої прямої:

Цій прямій належить точка М₂(2; 1; 0), тому її канонічне рівняння

Відповідь. і .

11