
- •1. Рівняння прямої з кутовим коефіцієнтом.
- •2. Властивості функцій, неперервних на відрізку
- •3. Алгоритм дослідження функції на екстремум.
- •Метод інтегрування заміни змінної у визначеному інтегралі.
- •Скалярний векторний добуток. Властивості векторного добутку.
- •2.Теорема про зв'язок між нескінченно малими та нескінченно великими функціями.
- •1. Матриці, основні поняття. Різновиди матриць.
- •2. Задачі, які приводять до поняття похідної: задача про продуктивність праці, задача про кутовий коефіцієнт дотичної.
- •3. Загальна схема побудови графіка функції за допомогою похідної.
2. Задачі, які приводять до поняття похідної: задача про продуктивність праці, задача про кутовий коефіцієнт дотичної.
Про продуктивність праці: нехай функція V=V(t) виражає кількість випущеної продукції V за час. Потрібно знайти продуктивність праці в момент часу t0.За період часу від t0 до t0+∆t кількість випущеної продукці Змінитися від значення V0=V(t0) до значення V0+∆V= V(t0+∆t),тоді середня продуктивність праці зросте за цей період часу Vсереднє=∆V/∆t.Миттєву продуктивність праці Vм у момент часу t0 можна визначити як граничне значення середньої продуктивності за період часу від t0 до t0+∆t при ∆t→0.
Про
кутовий коефіцієнт дотичної: Розглянем
графік функції y=f(x)
і 2 точки М0(х0;у0) та М1(х1;у1).Тоді ∆х=х1-х0
і ∆у=у1-у0.Проведем січну М0М1.кутовий
коефіцієнт січної tg(φ)=∆x/∆y.Zroj
∆x→0
то

Дотичною до графіка функції в точці М0 називається граничне положення січної,яка проходить через точку М0 та довільну точку М1 графіка за умови ,що М1 прямує вздовж графіка до М0.
3. Загальна схема побудови графіка функції за допомогою похідної.
1. Область визначення функції, точки перегину з осями координат.
2. Дослідження функції на парність (непарність), періодичність.
3. Знаходження асимптот графіка функції.
4. Дослідження ф-ції на монотонність, екстремум.
5. Дослідження на опуклість, вгнутість та точки перегину графіка функції.
6. Побудова графіка функції.4. Застосування визначеного інтеграла до обчислення площ фігур, обмежених лініями.
Якщо
на [a,
b]
функції
 і
і
 неперервні, то площа області, обмеженої
знизу графіком функції
,
зверху - графіком функції
,
зліва - прямою
неперервні, то площа області, обмеженої
знизу графіком функції
,
зверху - графіком функції
,
зліва - прямою
 ,
справа - прямою
,
справа - прямою
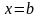 обчислюється за формулою:
обчислюється за формулою: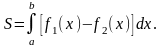
Якщо
на [a,
b]
функції
 і
і
 неперервні, то площа області, обмеженої
зліва графіком функції
,
справа - графіком функції
,
знизу - прямою
неперервні, то площа області, обмеженої
зліва графіком функції
,
справа - графіком функції
,
знизу - прямою
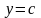 ,
зверху - прямою
,
зверху - прямою
 обчислюється за формулою:
обчислюється за формулою:


5. Степеневі ряди. Теорема Абеля.
Степеневим рядом називають функціональний ряд виду a0+a1(x-x0) +a2(x-x0)2+…+an(x-x0)n+…=(n=0∑∞)an(x-x0)n, або при х=0 ряд виду a0+a1x+a2x2+…+anxn+…= (n=0∑∞)anxn, де x0,a0,a1,… - дійсні або комплексні числа.
Теорема Абеля: Якщо ряд (n=0∑∞)anxn збігається при х=x1, то він збігається для всіх х, що задовольняють нерівність |x|<|x1|.
Якщо ряд (n=0∑∞)anxn розбігається при х=x2, то він розбігається для всіх х, що задовольняють нерівність |x|>|x2|.
