24.Первый метод Ляпунова.

Этот метод применяется для исследования устойчивости линейных и линеаризованных систем. Пусть уравнение движения линеаризованной системы управления записано для регулирования величины y(t) при наличии управляющего воздействия g(t) при отсутствии возмущения. (a0*pⁿ+a1*p^(n-1)+..+a_n-1*p+a_n)y(t)=

(b0*p^m+b1*p^(m-1)+..+b_m-1*p+b_m)g(t).

Процесс управления определяется решением дифуравнения как суммы двух решений

y(t)=yb(t)+yn(t), yb – вынужденная составляющая, yn – перех-я.

Устойчивость систем зависит от корней характеристического уравнения, поскольку его решение есть сумма экспоненциальных функций:

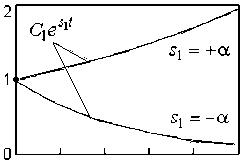
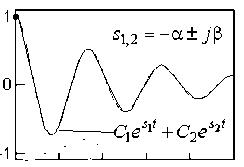
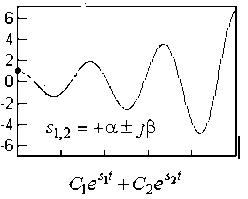
Рассмотрим варианты свободного движения систем от ненулевого начального положения. Заметим, что

где: А и φ  новые постоянные интегрирования, α  показатель затухания, β круговая частота затухающих колебаний.

Управляемость и наблюдаемость системы в изложенном смысле не всегда совпадает с практическими представлениями. Даже если какая-либо фазовая координата Мб вычислена по доступным для измерения выходным величинам, то обработка измеренных величин Мб сложной или затрудненной при наличии помех. Поэтому практически наблюдаемыми координатами обычно считают те, которые Мб измерены непсредственно датчиками различных типов.

25. Теоремы первого метода Ляпунова.

Ни одна реальная система не является строго линейной. Линейные характеристики получаются путем линеаризации реальных характеристик и уравнений. При разложении в ряд Тейлора учитываются линейные члены и отбрасываются члены высших порядков, которые для малых отклонений считаются пренебрежимо малыми. Обоснование законности такой линеаризации содержатся в теоремах 1 метода Ляпунова:

Теорема первого метода Ляпунова обосновывают законность линеаризации система управления.

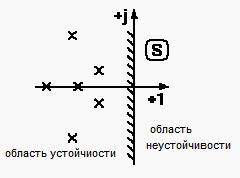
1.если характеристическое уравнение линеаризованной системы имеет все корни с отрицательными вещественными частями, то реальная система будет также устойчивой.

2.если характеристическое уравнение линеаризованной системы имеет хотя бы один корень с “+” вещественной частью, то реальная система будет также неустойчивой

3.при наличии нулевых и чисто мнимых корней, поведение реальной системы не всегда даже качественно определяется ее линеаризованными уравнениями. При этом даже малые нелинейности могут коренным образом влиять на вид переходного процесса, сделав систему устойчивой или неустойчивой

26.Второй (прямой) метод Ляпунова.

Ду системы управления в форме уравнений 1 порядка для переходного процесса в отклонениях и при постоянных значениях возмущающего f=f⁰ и задающего g=g⁰ воздействиях.

Где функции Х₁,Х₂…,Х_n – произвольны, содержат любые виды нелинейности, но всегда удовлетворяют условию Х1=Х2=..=Хn=0 при х1=х2=..=хn=0 (10).

Поскольку в установившемся состоянии все отклонения переменных и их производных =0 согласно определению этих отклонений.

Пусть имеется функция нескольких переменных V=V(x₁,x₂..x_n).

В каждой точке н-мерного фазового пространства V б иметь некоторое определенное значение. Функция V называется занкоопределенной в некоторой области, если она во всех точках этой области вокруг начала координат имеет один и тот же знак и нигде не обращается в 0, кроме самого начала координат.

Функция называется знакопостоянной. Если она сохраняет один и тот же знак, но м обращаться в 0 не только в начале координат. Но и в других точках данной области.

Функция V называется знакопеременной, если она в данной области вокруг начала координат м иметь разные знаки.