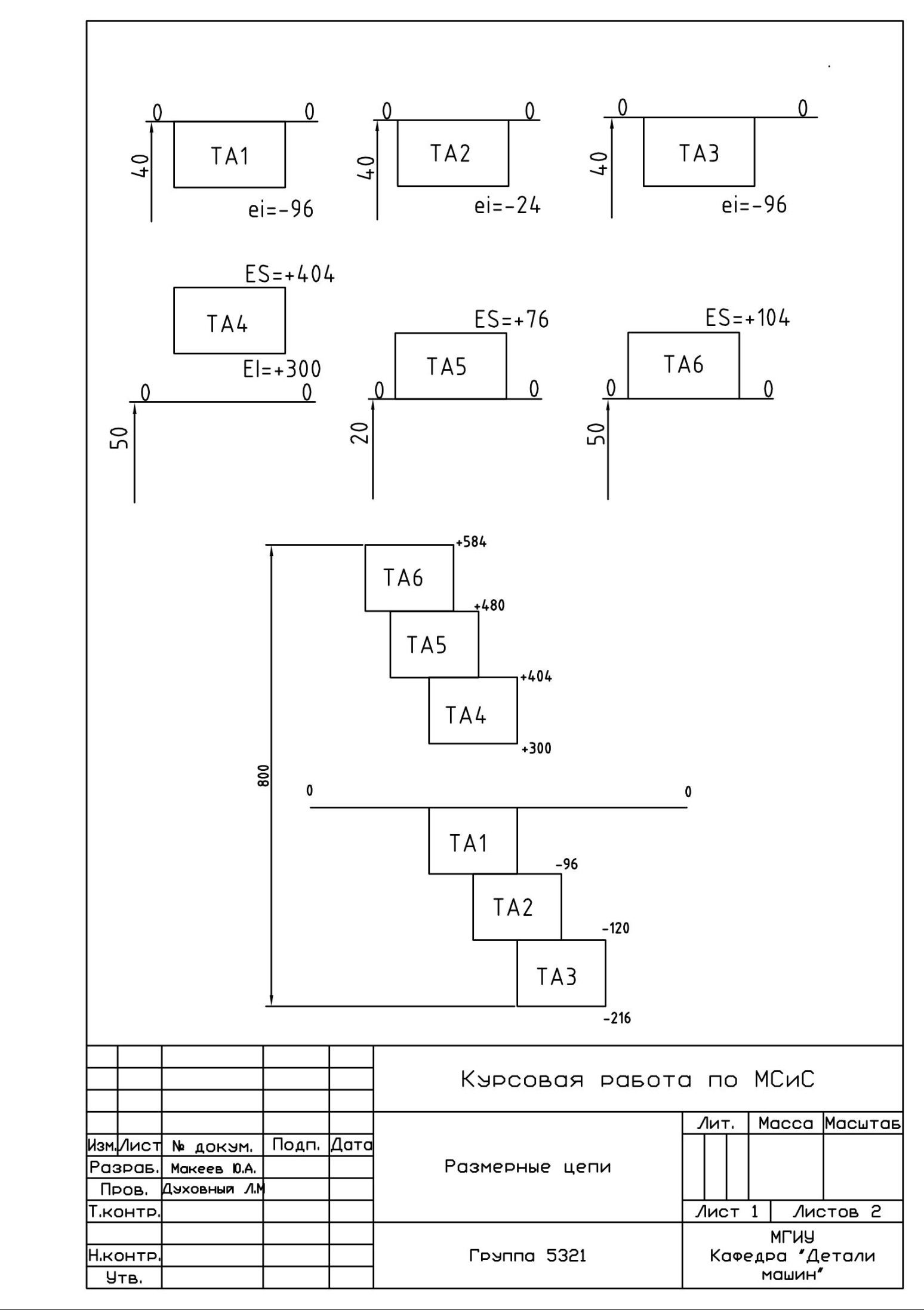
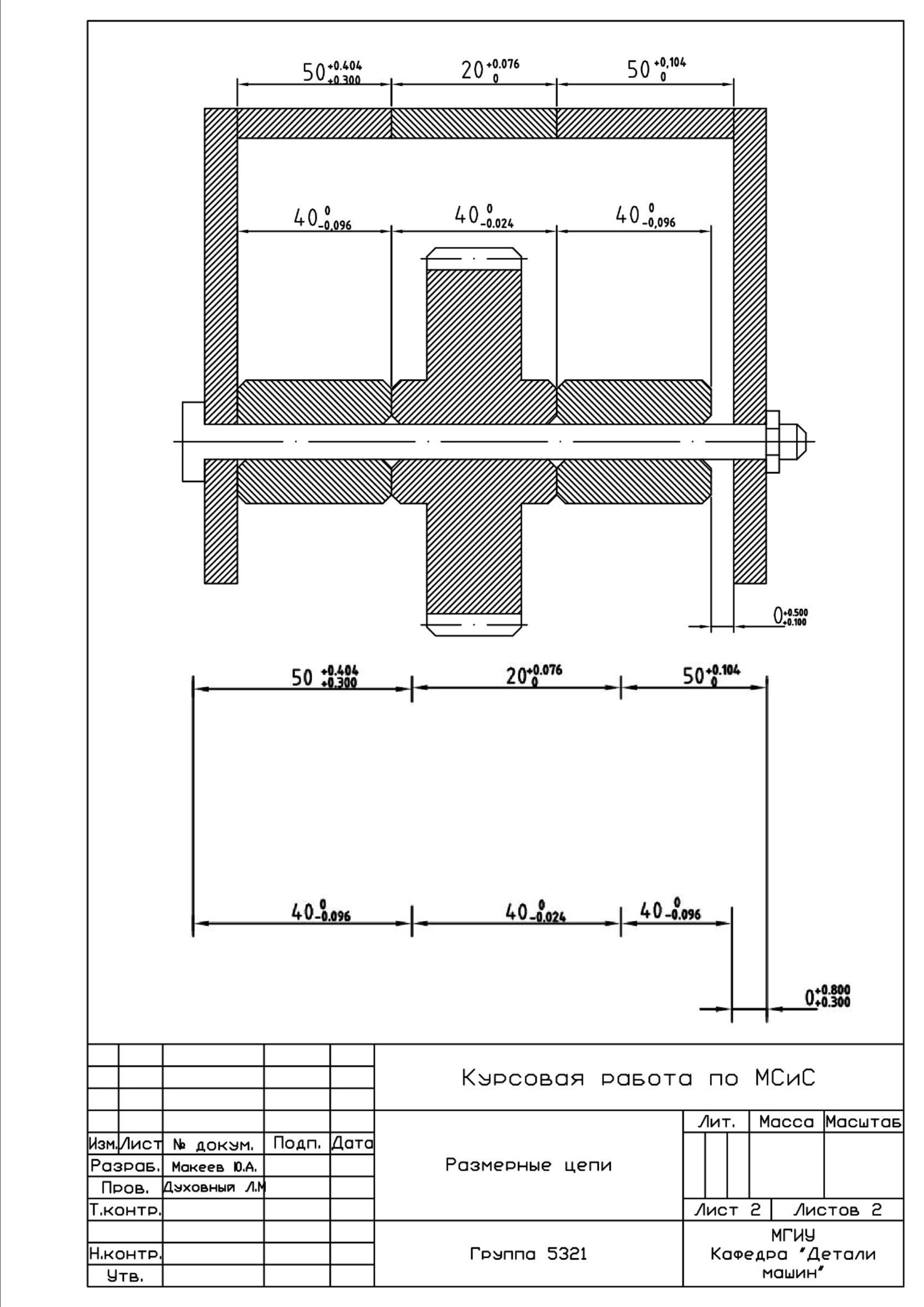
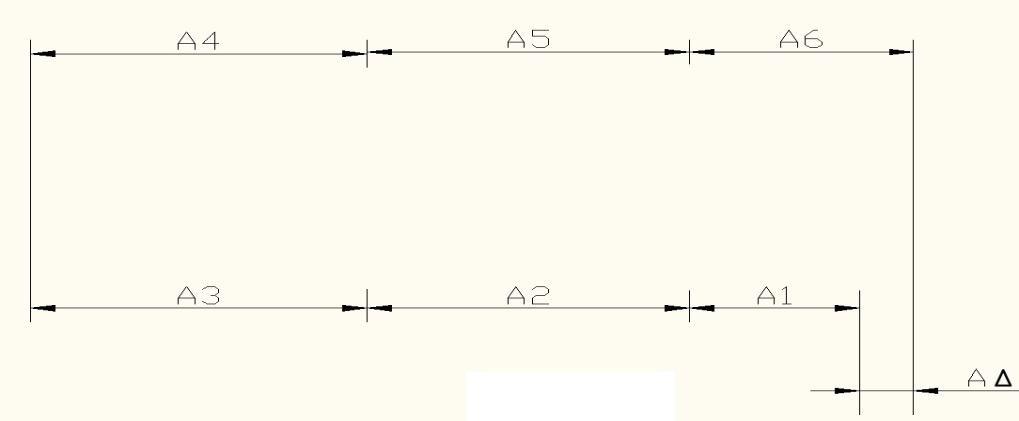
Расчет размерных цепей методом полной взаимозаменяемости.
Вариант |
Номинальные значения размеров узла в мм. |
АΔ=0 |
||||||
А1 |
А2 |
А3 |
А4 |
А5 |
А6 |
EIΔ |
ESΔ |
|
12 |
|
40** |
|
50 |
20 |
50 |
0,3 |
0,8 |
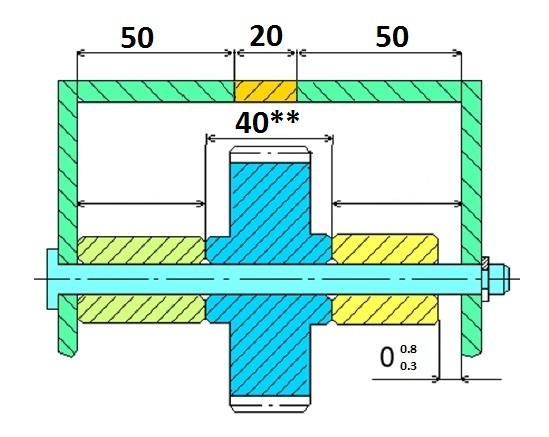
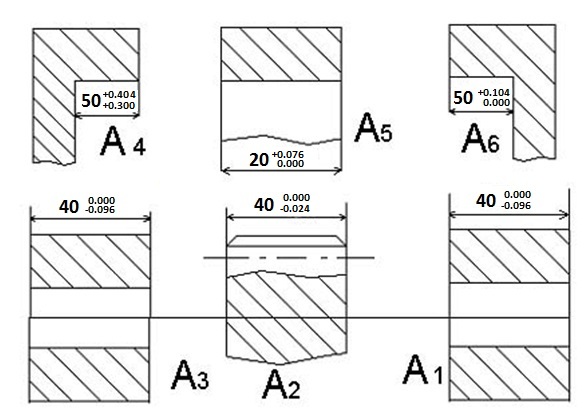
Определяются значения исходного размера.
Исходный-замыкающий размер дан по условию задачи, номинальное значение – АΔ = 0, с учётом отклонений EI=0,3 и ES=0,8.
Допуск замыкающего размера
TA=ESA-EIA=0,800-0,300=0,500мм=500мкм заносим в таблицу 1.
Составляется уравнение размерной цепи в номиналах для линейной размерной цепи:
АΔ
=
 Ai
ув –
Ai
ув –
 Ai
ум
Ai
ум
Для рассматриваемого случая: АΔ = (А1 + А2 + А3) – (А4 + А5 + А6)
A1=A3=(50+20+50-40)/2=40
По условию задачи необходимо обеспечить полную взаимозаменяемость деталей узла по рассматриваемым линейным размерам. Так как номинальные размеры отдельных звеньев различны, то применим метод одного квалитета с условием расчета на максимум и минимум.
Квалитет изготовления размеров, можно определить через коэффициент точности по формуле

Таблица 1.
Номинал. Размер |
i |
TAi, мкм |
TAi, мкм |
TAi, +TAi, мкм |
Расположение поля допуска |
0Ai мкм |
ESAi, мкм |
EIAi, мкм |
|
Ai |
Значен. |
||||||||
A |
0 |
- |
500 |
- |
- |
|
550 |
800 |
300 |
A1 |
40 |
1,57 |
96 |
0 |
96 |
|
48 |
0 |
96 |
A2 |
40** |
- |
25 |
-1 |
24 |
|
12 |
0 |
24 |
A3 |
40 |
1,57 |
96 |
0 |
96 |
|
48 |
0 |
96 |
A4 |
50 |
1,71 |
105 |
-1 |
104 |
|
? 52 |
? 404 |
? 300 |
A5 |
20 |
1,24 |
76 |
0 |
76 |
|
38 |
76 |
0 |
A6 |
50 |
1,71 |
105 |
-1 |
104 |
|
52 |
104 |
0 |
Σ |
240 |
7,8 |
503 |
3 |
500 |
- |
|
|
0 |
Вычислим значения чисел i и запишем в таблицу 1.
ii
= 0.45 +
0.001Ai
ср
+
0.001Ai
ср
i1
= 0.45 +
0.001*40 = 1,57
+
0.001*40 = 1,57
i3 = 0.45 + 0.001*40 = 1,57
i4
= 0.45 +
0.001*50 = 1,71
+
0.001*50 = 1,71
i5
= 0.45 +
0.001*20 = 1,24
+
0.001*20 = 1,24
i6 = 0.45 + 0.001*50 = 1,71
Имея, допуск замыкающего размера и получив сумму чисел i, можно определить аср
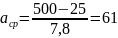
Определяются допуски на составляющие размеры.
 =
= ×
×





Проверочный расчет необходимо провести по формуле,
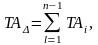 где должно
удовлетворяться уравнение:
где должно
удовлетворяться уравнение:

Но (96+25+96+105+76+105) - 500 = 3
Необходимо
провести корректировку допусков TAi,
в соответствии с уравнением
 для данного решения
для данного решения
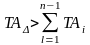 ,
поэтому уменьшаем некоторые допуски.
,
поэтому уменьшаем некоторые допуски.
Окончательно полученные значения допусков внесём в столбец таблицы TAi+TAi.
 =
=
 –
–

 =
=
 –
–

Δ0 АΔ = Δ0 Аi ув – Δ0 Аi ум,
Необходимо один из размеров принять как увязочный и положение поля его допуска вычислить. Пусть это будет допуск размера TА4
Установим допуски и соответствующие отклонения ES, EI остальных размеров.
Решить задачу удобно через уравнение середин полей допусков
Δ0 АΔ = Δ0 Аi ув – Δ0 Аi ум

0A = (0A4 + 0A5 + 0A6) - (0A1 + 0A2 + 0A3);
Середина поля допуска замыкающего размера определяется по формуле:
 =550
мкм
=550
мкм
Введем численные значения размеров в уравнение середин полей допусков и вычислим середину поля допуска увязочного размера 0A4:
0A=(0A4 + 0A5 + 0A6) - (0A1 + 0A2 + 0A3)
550 = Х+38+52+48+12+48
X = 352 мкм
Вычислим, через допуск, отклонения увязочного размера A4:
ESA4= 352+52 = 404
EIA4= 352-52 = 300