Формулы для определения давления металла на валки
Задача состоит
в определении силы полного давления
металла на валок
,
которую вычисляют по общеизвестной
формуле:
(72- IV)
или
, (73- IV)
где
– среднее удельное давление.
Ниже приведены
ориентированные значения полного
давления
для
некоторых станов [37]:
Блюминги………………………………………………..5–15(500–1500)
Слябинги…………………………………………………6–18(600–1800)
Непрерывные тонколистовые станы…………………..5–20(500–2000)
Рельсобалочные и крупносортные станы……………..1,5–7(150–700)
Среднесортные станы…………………………………..0,5–2(50–200)
Мелкосортные станы…………………………………0,15–0,60(15–60)
Определение среднего удельного давления представляет в ряде случаев значительные трудности, в основном из-за недостатка опытных данных по механическим свойствам металла.
В общем виде полное удельное давление равно:
где
–
непосредственно действующее со стороны
металла удельное давление, зависящее
от внутреннего сопротивления металла
деформации, химического состава металла
и его физического состояния, определяемого
температурой нагрева, структурой,
скоростью и степенью деформации;
–
коэффициент, учитывающий влияние внешних
сопротивлений, зависящих главным образом
от параметра формы очага деформации
,
и коэффициента трения
между
прокатываемой полосой и валками.
Формулы для определения среднего удельного давления металла на валки, получившие наибольшее распространение, приведены ваше.
В Технической литературе приведено большое количество формул для определения контактного давления при прокатке. Из теоретических формул, разработанных советскими учеными, следует отметить формулы А.И. Целикова, А. А. Королева, Е.С. Рокотяна, А.П. Чекмарева, В.С. Смирнова и др. Все они получены путем решения дифференциального уравнения контактных напряжений, действующих на металл в зоне деформации.
Формулы для определения контактного давления p при горячей прокатке
Формула А.И. Целикова:
,
где
;
при
;
;
при
(см. рис. IV.7);
при
;
при
;
при
;
,
где коэффициент учитывает влияние 2; nb– изменение влияния внешнего трения в связи с уширением; n– влияние напряжённого состояния; n– влияние внешнего трения; n– влияние внешних зон; n– влияние натяжения; nб–влияние боковых внешних зон; S и S0– площади поперечного сечения полосы и её обжимаемой части.
Формула А.А. Королёва [22]:
;
;
;
;
;
при
;
,
где
–
коэффициент, характеризующий наличие
зон скольжения и прилипания;
–
протяжённость зоны прилипания.
Формула В.С. Смирнова [4]:
;
при
;
при
;
;
При наличии одной
зоны прилипания, т.е. при
или
при
,
;
.
При наличии зон скольжения
;
,
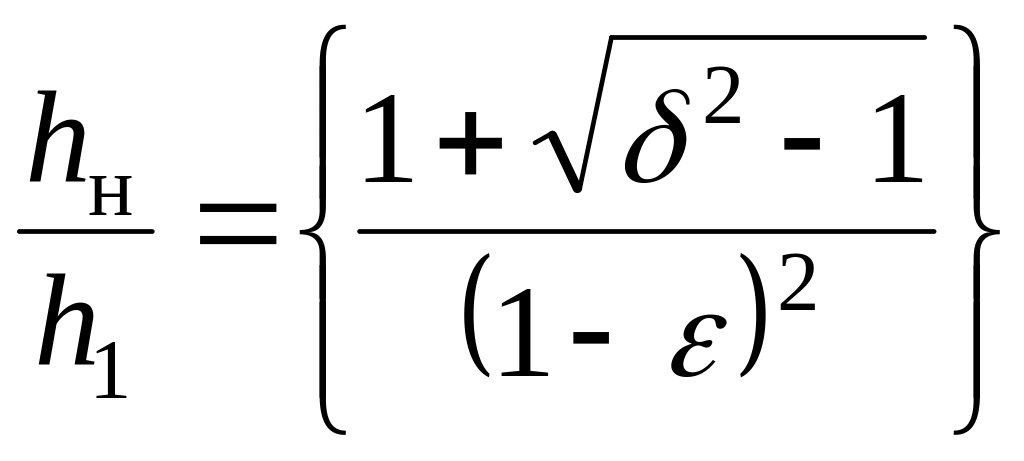где n–
коэффициент, учитывающий влияние
контактного трения и натяжения;
–
коэффициент трения при установившемся
процессе прокатки;
,
–
толщина полосы на границах зон отставания
и опережения.
Формула Экелунда [37]:
,
где
;
;
;
,
где
–
коэффициент, учитывающий внешнее трение;
–
сопротивление деформации при статическом
сжатии;
–
коэффициент вязкости металла;
–
коэффициент, зависящий от скорости
деформирования
.
При
,
равном 6;10;15 и 20м/c, коэффициент
соответственно
равен 1;0,8;0,65 и 0,6;
–
скорость деформации, с-1;
–
содержание углерода, марганца и хрома
в металле, %.
Формула С.И. Губкина [21]:
,
где
;
,
где
–
скоростной коэффициент, при
;
при
;
при
;
–
температурный коэффициент (верхний
предел принимают для твёрдых растворов
с большой концентрацией);
–
температура плавления С;
–
коэффициент неравномерности распределения
температурных напряжений;
–
временное сопротивление, соответствующее
температуре
и скорости деформирования
[57];
–
коэффициент трения.
Формула Гелеи [2]:
,
где
–
сопротивление линейной деформации,
–
для нелегированных углеродистых сталей;
–
для высокоуглеродистых сталей; содержащих
и
;
–
коэффициент, зависящий от
(см. рис. IV.10) ;
–
окружная скорость валков,
.
Формула А.П. Чекмарёва [28]:
,
где
,
–
коэффициент формы калибра; П–периметр
калибра; b– ширина калибра
по разъёму;
см. формулу А.И. Целикова; –
коэффициент Лодэ.
Значение коэффициента формы для различных калибров [28]:
Квадратный…………………………………………………….1,41
Ромбический, с углом при вершине, град:
100……………………………………………………1,30
110……………………………………………………1,20
120……………………………………………………1,15
Круглый………………………………………………………..1,40
Овальный
однорадиусный с
,
равном:
1,5…………………………………………………….1,27
2………………………………………………………1,15
3………………………………………………………1,09
Овальный плоский…………………………………………..1,1–1,15
Шестигранный…………………………………………………1,15
Угловой и зетовый:
чистовые……………………………………………...1,41
черновые……………………………………………1,2–1,25
Калибры двутавровой балки:
№30………………………………………………….1,7–1,9
№16………………………………………………….2,1–2,2
Калибры швеллера:
№30………………………………………………….1,7–1,8
№16………………………………………………….1,8–2,0
№8………………………………………………….…2,1–2,3
Рельс Р–50……………………………………………………..2–2,1
Шпунт Л–5…………………………………………………….1,8–2,1
Формула Е.С. Рокотяна [2]:
,
где
–
удельный расход энергии за данный проход
с вычетом расхода энергии на трение в
механизме прокатного стана,
;
–плотность
металла,
.
Формула А.А. Королёва [22]:
,
где
при
,
где
–
коэффициент напряжённого состояния
при прокатке в калибрах; a
и b– коэффициенты, зависящие
от формы калибра,
и
,
когда имеет место прокатка простых
профилей (узкая полоса, плоский овал ).
Схема деформации
соответствует плоской (двухмерной):
и
для
овальных и круглых калибров;
и
для квадратных и ромбических калибров,
для фасонных закрытых калибров.
При
величина
.
Формулы
для расчёта контактного давления
при
холодной прокатке.
Формула А.И. Целикова [2] без учёта наклёпа:
;
;
;
;
,
где
–
заднее натяжение;
–
переднее натяжение;
,
–
коэффициенты натяжения.
Формула А.И. Целикова [2] с учётом наклёпа:
где
;
.
Формула А.А. Королёва [22]:
;
;
;
;
,
где
–
коэффициент упрочнения;
–
коэффициент, характеризующий положение
нейтрального сечения.
Формула Хессенберга и Симса [2]:
.
Формула Стоуна [2]:
.
Формула Е.С. Рокотяна [2]:
;
;
;
;
,
где
–
контактное давление без учёта натяжения;
–
основание натуральных логарифмов;
;
.
Этими формулами рекомендуется пользоваться при определении величины как в случае горячей и холодной прокатки широких полос, так и при прокатке в калибрах. Результаты расчета по этим формулам различаются незначительно.
Из разработанных зарубежными учеными практическое применение нашли методы Кармана, Тринкса, Экeлунда, Гелеи, Бленда, Форда, Орована, Симса и др. Анализ этих методов, приведен в работах [2,3,22, 23].В основном они с некоторыми уточнениями (а чаще упрощениями) дополняют изложенный выше метод.
Известно также большое количество эмпирических и полуэмпирических формул, полученных на основании математической обработки экспериментальных данных. 0бобщенного характера эти формулы (например Экелунда, Гелеи и др.) иметь не могут, и область их применения ограничена условиями, в которых получены входящие в них коэффициенты.
Для пользования теоретическими формулами в технической литературе приведены номограммы, однако при современных ЭВМ удобнее пользоваться численными методами расчета.