Государственное образовательное учреждение высшего
профессионального образования
Уфимский государственный авиационный технический
университет
СБОРНИК ЗАДАЧ
по учебной дисциплине
«Лопастные гидромашины и гидродинамические передачи»
Направление подготовки дипломированного специалиста
552700 (150800) «Гидравлическая, вакуумная и компрессорная техника»
Специальность 552702 (150802) «Гидравлические машины, гидроприводы и гидропневмоавтоматика»
(очная форма обучения)
Уфа 2011
Составитель:
___________ Еникеев Г.Г. ________2011 г
подпись ФИО дата
Рассмотрено на заседании кафедры “Прикладная гидромеханика”
«____» 2011 года (протокол №_______).
Зав. кафедрой ПГМ
____________________ Целищев В.А.
подпись
«_____» _______________ 2011г.
дата
Рассмотрено на заседании научно-методического Совета
по направлению подготовки дипломированного специалиста (бакалавра, магистра)
552700 (150800) «Гидравлическая, вакуумная и компрессорная техника»
«____» __ 2011 г. (протокол № ________).
Председатель научно-методического Совета
___________ д.т.н., профессор, Целищев В.А.
СОДЕРЖАНИЕ
1 |
Кинематика и динамика потока в рабочем колесе лопастной гидромашины. Основное уравнение лопастных гидромашин
|
4 |
2 |
Методы теории подобия в лопастных насосах
|
13 |
3 |
Кавитация в лопастных насосах
|
18 |
4 |
Характеристики насосов. Параллельная и последовательная работа насосов на сеть. Работа насоса на разветвленный трубопровод |
22 |
.
1. Кинематика и динамика потока в рабочем колесе лопастной гидромашины. Основное уравнение лопастных гидромашин.
Поток
жидкости в проточной части лопастной
гидромашины носит пространственный
характер. Скорость потока в любой точке
пространства проточной части
представляется вектором V
в абсолютном
движении. Для лопастных гидромашин
используется система координат
вращающаяся с угловой скоростью
и поток рассматривается в относительном
движении. Вектор скорости потока в
относительном движении W
связан с
вектором абсолютной скорости V
следующим
векторным соотношением:
V=W+U (1.1)
где U вектор переносной скорости.
То есть сумма относительного и переносного движений дает абсолютное движение жидкости.
Для графического представления векторов скоростей используются следующие системы координат: декартова система координат, полярная система координат, цилиндрическая система координат, естественная система координат.
Естественная
система координат позволяет представить
пространственный поток разделив его
на два: на поток протекания , определенный
меридиональной составляющей скорости
и циркуляционный поток ,определенный
составляющей вектора абсолютной
скорости
на
направление вектора переносной скорости
U.
Из уравнения (1.1) следует, что скорости V,W, и U образуют треугольник скоростей. На рис. 1.1 изображен треугольник скоростей для произвольной точки К внутри проточной части рабочего колеса . Согласно схеме бесконечного числа лопаток, относительная скорость W направлена по касательной к профилю лопатки. Окружная (переносная) скорость U направлена по касательной к окружности, на которой расположена рассматриваемая точка в сторону вращения рабочего колеса. Вектор абсолютной скорости V является замыкающим в треугольнике скоростей и направлен он к концу вектора W.
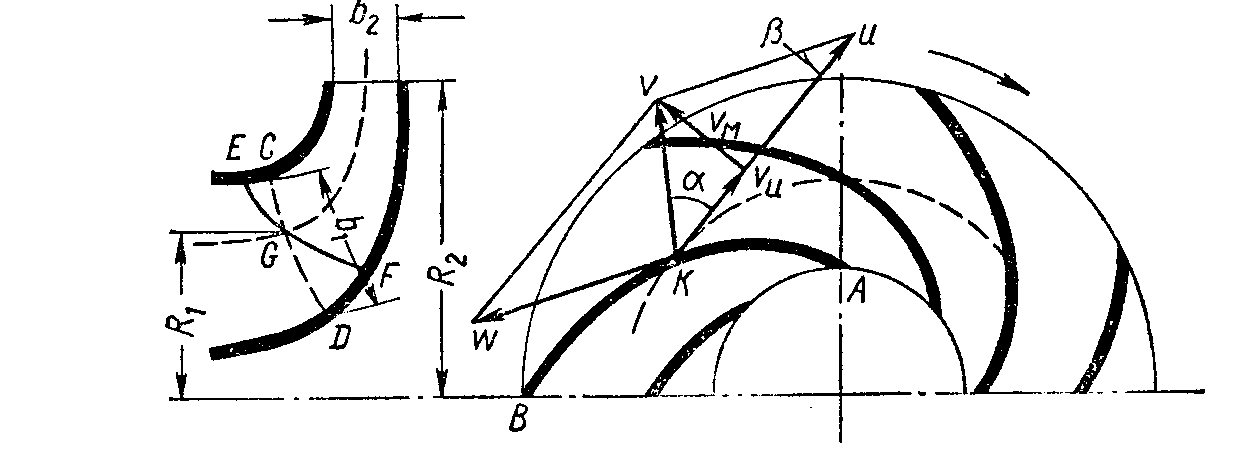
Рис 1.1. Кинематики потока в рабочем колесе
На рис 1.1 введены следующие обозначения:
-угол
между абсолютной V
и переносной
U
скоростями
жидкости ;
-угол
между относительной скоростью W
и отрицательным
направлением переносной скорости
U
жидкости.
-угол
между касательной к лопатке и отрицательным
направлением переносной скорости U
жидкости.
-ширина
лопатки на входе и выходе рабочего
колеса.
-
радиус, на котором расположен центр
тяжести линии CD.
-
периферийный радиус рабочего колеса.
Меридиональную
скорость
,
необходимую для построения треугольника
скоростей можно определить по следующей
формуле:
(1.2)
где
-расход жидкости через колесо;
-площадь
нормального сечения меридионального
потока.
С
учетом коэффициента стеснения потока
лопатками
и объемного коэффициента полезного
действия
,
меридиональная составляющая скорости
определяется по следующей формуле:
(1.3)
где
-подача
насоса
Входящий в уравнение ( 1.3) коэффициент стеснения потока лопатками определяется
последующей формуле:
(1.4)
где: Z- число лопаток рабочего колеса
-толщина
лопатки по нормали к средней линии
профиля (см. рис. 1.2)
Рис 1.2 Входной участок лопатки рабочего колеса
Окружная скорость рабочего колеса U подсчитывается по формуле:
U=
R
(1.5)
При бесконечном числе лопаток теоретический напор насоса
(1.6)
Влияние конечного числа лопаток на теоретический напор насоса можно учесть поправкой
Стодолы-Майзеля, т.е.
(1.7)
или поправкой К. Пфлейдерера, т.е.
(1.8)
Если
известен гидравлический КПД
, то нетрудно перейти от теоретического
напора
к напору
,
для насоса
(1.9)
для турбины
(1.10)
Момент на рабочем колесе лопастной гидромашины можно определить по параметрам потока
(1.11)
В выражении (1.11) знак плюс относится к рабочим колесам насосов , а знак минус к рабочим колесам турбины
Гидравлическая мощность турбины вычисляется из следующего соотношения
(1.12)
или
(1.13)
здесь знак плюс относится к насосам , а знак минус относится к турбинам