Проверка устойчивости по критерию михайлова
Только устойчивые АСР являются работоспособными, поэтому основное требование к АСР – это устойчивость.
Устойчивыми называются такие системы, которые после выведения их из равновесного состояния возмущающими или задающими воздействиями, возвращаются к исходному состоянию после снятия действия этой причины.
Для того чтобы переходной процесс затухал все корни характеристического уравнения должны находится в левой комплексной полуплоскости или иначе – они должны быть отрицательные или иметь отрицательную вещественную часть. Мнимая ось является границей устойчивости. Если хотя бы один корень будет находиться в правой комплексной полуплоскости, то система будет неустойчива.
Определить корни уравнения высшего порядка мы не можем, поэтому в ТАУ разработаны критерии устойчивости, которые позволяют, не определяя корней, сделать вывод об устойчивости системы. Делятся эти критерии на алгебраические и частотные. С математической точки зрения они равнозначны.
Критерий Михайлова относится к частотным критериям устойчивости.
Для определения устойчивости АСР прежде всего необходимо знать характеристическое уравнение замкнутой АСР:
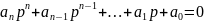
В основе критерий Михайлова лежит принцип аргумента:
если есть произведение комплексных чисел, то аргумент будет равен суме аргументов каждого из сомножителей.
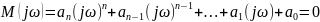
Система автоматического управления не будет иметь корней в правой комплексной полуплоскости, если годограф замкнутой системы будет проходить последовательно (против часовой стрелки), при изменении ω от 0 до +∞, n квадрантов и уходить в бесконечность при ω=∞ в том квадранте, какой порядок характеристического уравнения.
Чтобы
САУ была устойчива необходимо и
достаточно, чтобы при изменении ω
[0;∞) годограф Михайлова M(ϳω)
повернулся против часовой стрелки на
угол равный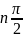
,
где n – порядок
характеристического уравнения замкнутой
системы.
Рассматривая на комплексной плоскости годограф Михайлова, условие устойчивости формируется так: система будет устойчива, если годограф Михайлова при изменении ω [0;∞) прошел последовательно n квадрантов в положительном направлении (против часовой стрелки) и нигде не проходил через начало координат.
Определим устойчивость системы с помощью критерия Михайлова:
Передаточная функция замкнутой АСР по каналу управления:
Отсюда характеристическое уравнение
Для критерия Михайлова необходимо
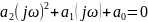
Четная степень ω – вещественная часть
Нечетная степень ω – мнимая часть
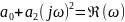
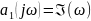
Чтобы найти точки пересечения с осью мнимых:
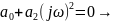0.014
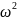60
=0
Рисунок 7. Годограф Михайлова
Так
как годограф Михайлова M(j
)
правильный, он последовательно прошел
два квадранта, и во втором ушел в
бесконечность, начался в
,
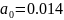следовательно – система устойчива.
Построение переходного процесса в аср.
Переходной процесс можно определить по передаточной функции замкнутой системы.
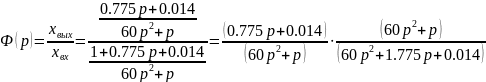
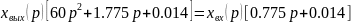
От изображения переходим к дифференциальному уравнению:
Данное уравнение решаем на ЭВМ методом Рунге-Кута.
Переходной процесс приведен на рисунке 7.