12.4. Понятие о вырождении "электронного газа"
Проанализируем функцию распределения Ферми – Дирака.
1
)
Пусть
,
т. е.
,
тогда при
,
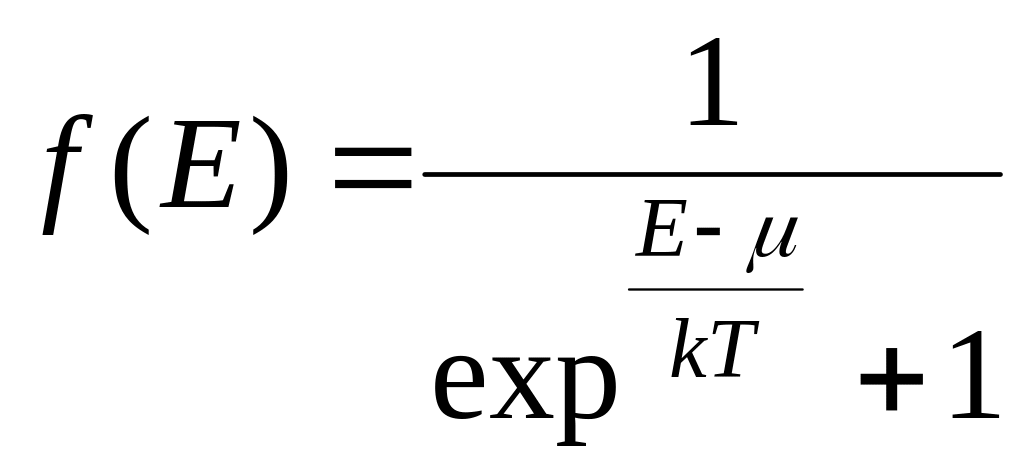
т. е. знаменатель стремится к бесконечности.
Тогда
.
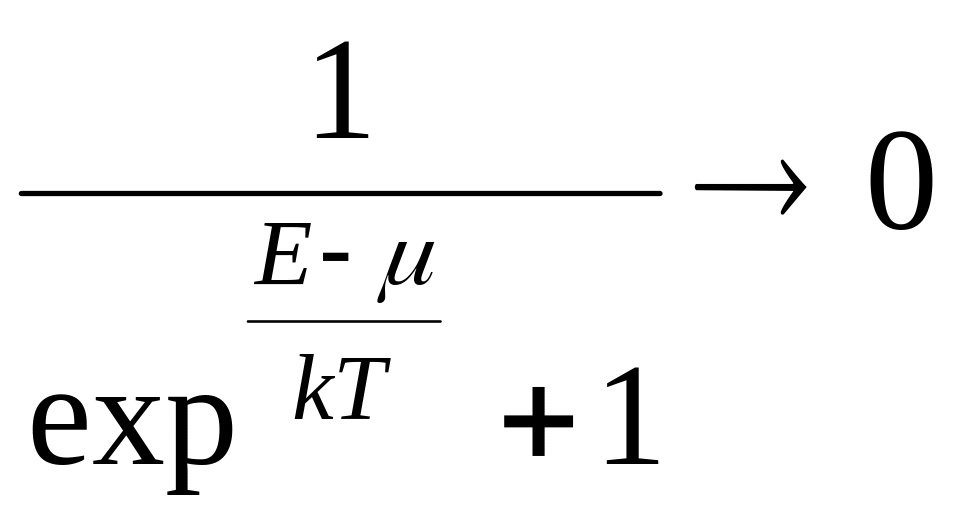2)
Пусть
,
т. е.
,
тогда
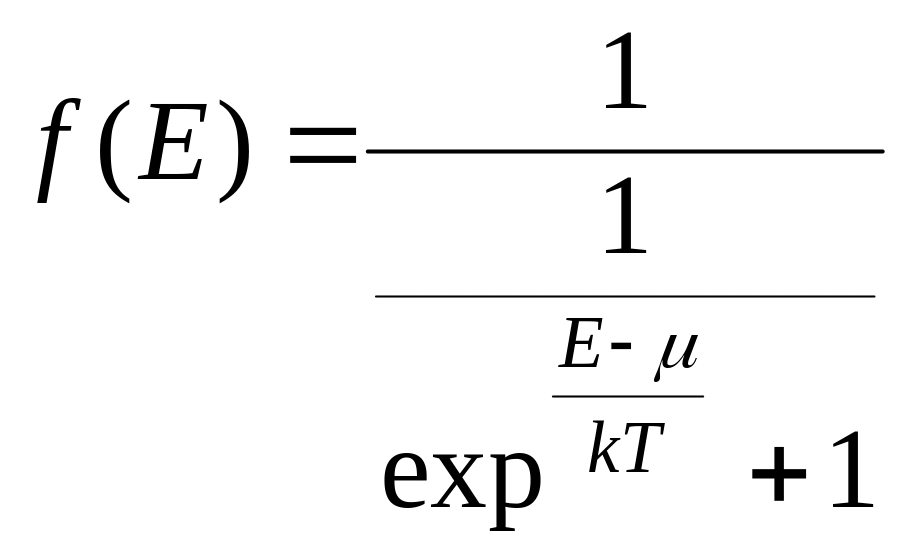и при тех же условиях
(
)
.
3)
При
для произвольных температур.
4
)
Согласно п.п. 1, 2 функция Ферми – Дирака
при Т = 0,К может быть представлена
графиком (см. рисунок), из которого
следует, что электроны в металле занимают
все энергетические уровни вплоть до
уровня
,
т. к. вероятность их заполнения равна
единице. Уровни с
остаются свободными, т. к.
(вероятность заполнения равна нулю).
5)
Уровень, вероятность заполнения которого
равна
т. е.
называется уравнением Ферми. Ему
соответствует
.
Следовательно, энергия Ферми представляет
собой максимальную энергию, которую
могут иметь электроны в металле при
абсолютном нуле.
и характеризует электрические свойства
металла.
6)
Если
,
то при
и
.
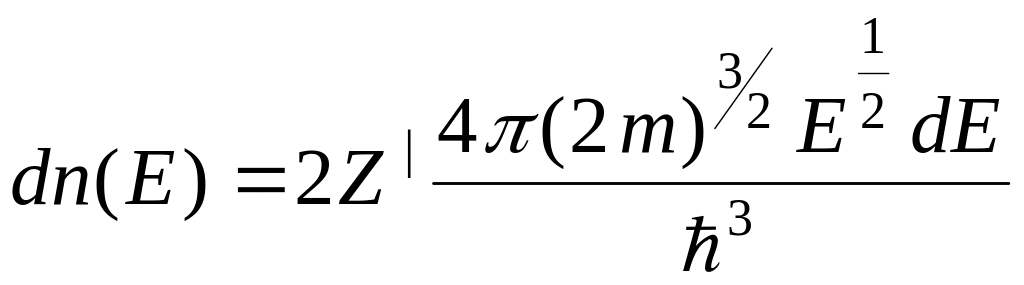После интегрирования
,
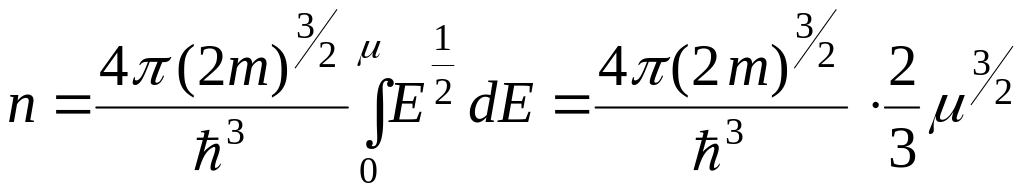т.
е. число свободных электронов в единице
объема металла. Из полученного выражения
следует, что
.
Как
показывает расчет, средняя энергия
электрона
.
После подстановки
.
Если
бы "электронный газ" был "обычным"
газом, то при обратной подстановке
или 5,4 эВ =
следовало,
что
.
Столь
высокие значения температуры
свидетельствуют о том, что свойства
"электронного
газа" резко отличаются от свойств
обычного газа, а его распределение не
подчиняется законам классической
механики, т. е. такой газ находится в
"вырожденном" состоянии. Здесь
- температура "вырождения".
7
)
Рассмотренное ранее условие
,
когда статистика Ферми – Дирака переходит
в статистику Максвелла – Больцмана -
есть условие снятия "вырожде -
ния". Вырождению электронов в металле способствует их ма -
лая масса (m = 10-31 кг) и высо -
кая концентрация (n 1028 м3),
а также низкая температура по сравнению с , при которой находится металл.