12.2. Функции распределения статистик
Основная задача любой физической статистики состоит в нахождении функции распределения по определенному параметру (составляющие импульса, импульс, энергия, скорость и т. д.), отвечающей равновесному состоянию системы.
В статистической физике доказывается, а мы приводим без доказательства, что
- в статистике Максвелла – Больцмана функция распределения по энергиям имеет вид (см. "Механика", Лекция 13)
или
,
-
в статистике Бозе – Эйнштейна
,
-
в статистике Ферми – Дирака
.
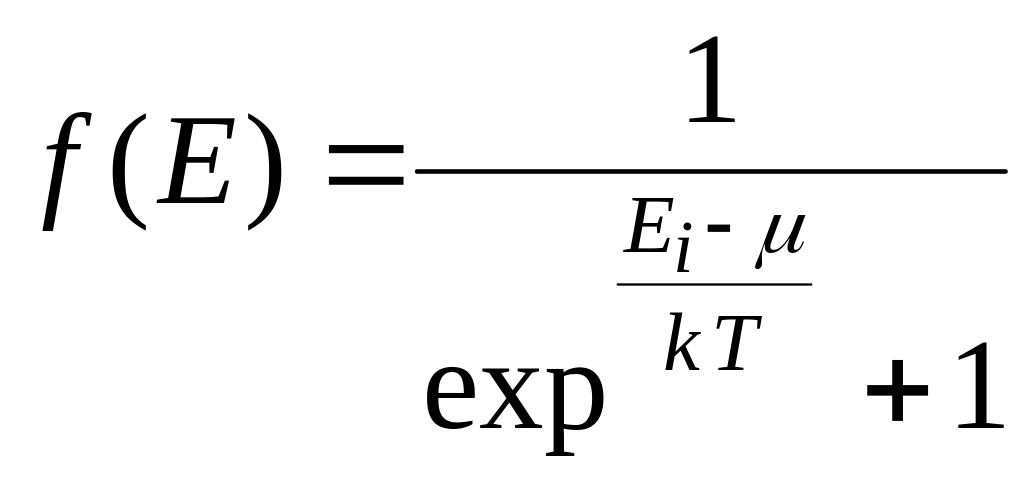Анализ.
1) Функция распределения по энергиям в статистике Максвелла – Больцмана – это распределение молекул идеального газа в фазовом пространстве, неподверженном действию силового поля.
2
)
В квантовых статистиках
- энергия
заполняемой ячейки,
- химический потенциал одной микрочастицы.
Для замкнутой термодинамической системы
(см. "Механика". Лекция 15)
.
Если
система незамкнута и осуществляется
массообмен
с
внешней средой, то
,
где
- из -
менение
числа частиц. С учетом выведенных
ранее
соотношений
.
При
- имеет
смысл
изменения
энергии при изохорно – изоэнтропийном
процессе.
3)
Г
рафики
функций распре –
деления частиц по энергиям для различных статистик приведены на рисунке.
4)
При
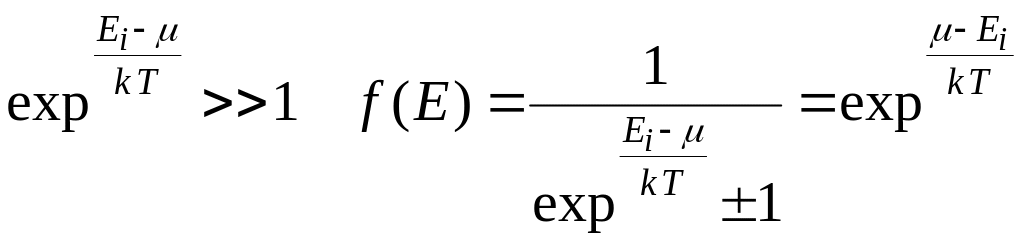или
,
т. е. квантовые статистики
переходят в классическую.
5) В квантовой механике, как и в классической, функции распределения имеют статистический (вероятностный) характер. Они показывают вероятность заполнения фазовых ячеек электронами (бозонами).
12.3. Распределение электронов по составляющим
импульса, по энергиям и по импульсам
Дано:
объем (
)
металла.
Найти:
,
т. е. число электронов, составляющие
импульса которых изменяются в пределах
.
В
пространстве импульсов (
)
построим элемент
объема
и разобъем
его на ячейки
,
тогда их
чис-
ло
(
)
будет
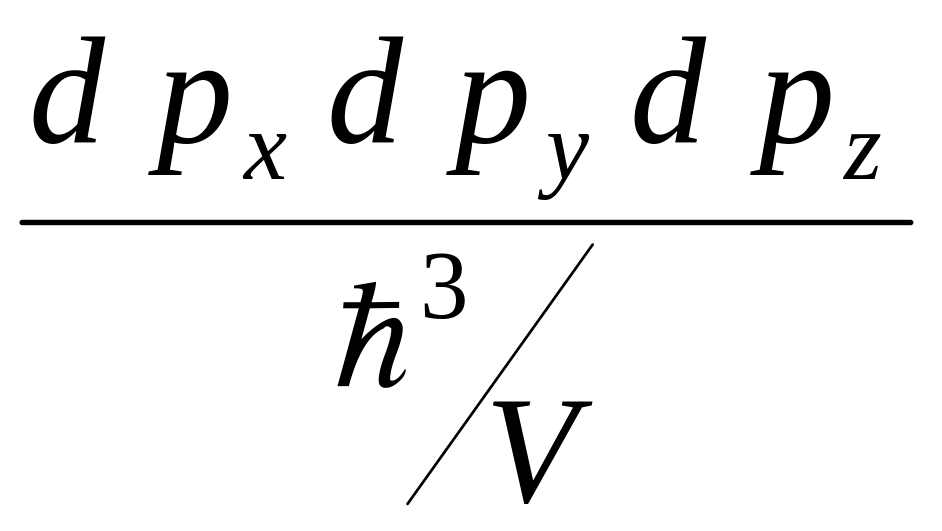или
.
Для единицы объема (число ячеек в единице объема)
.
Так
как вероятность заполнения этих ячеек
есть функция распределения Ферми –
Дирака, т. е.
,
а согласно принципу Паули в каждой из
них может разместиться только 2 электрона,
то
.
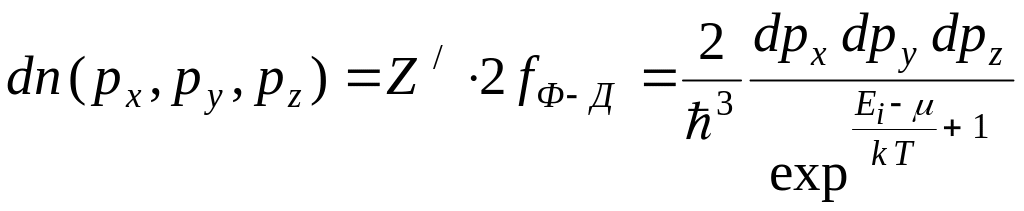Анализ:
1)
Полученное выражение позволяет расчитать
количество электронов, составляющие
импульса которых изменяются в пределах
.
2) Аналогичное выражение в статистике Максвелла – Больцмана есть (см. "Механика . . .". Лекция 13)
.
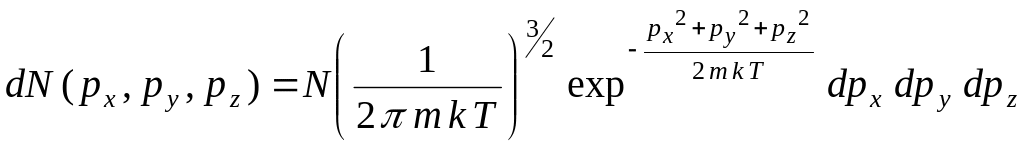3)
Величина
,
равная
,
есть функция распределения электронов
по составляющим импульса.
Найдем
число электронов (
)
в единице
объема (
)
металла,
энергия которых
заключена
в интервале от
до (
).
Д
ано:
объем металла.
Найти:
.
В пространстве импульсов постро -
им
две концентрические сферы с радиусами
(на рисун-
ке показан плоский случай). Этим сферам соответствуют энергии
. Объем шарового слоя меж-
ду
сферами (заштрихован)
и в нем разместится
-
элементарных
ячеек размером
,
т. е.
.
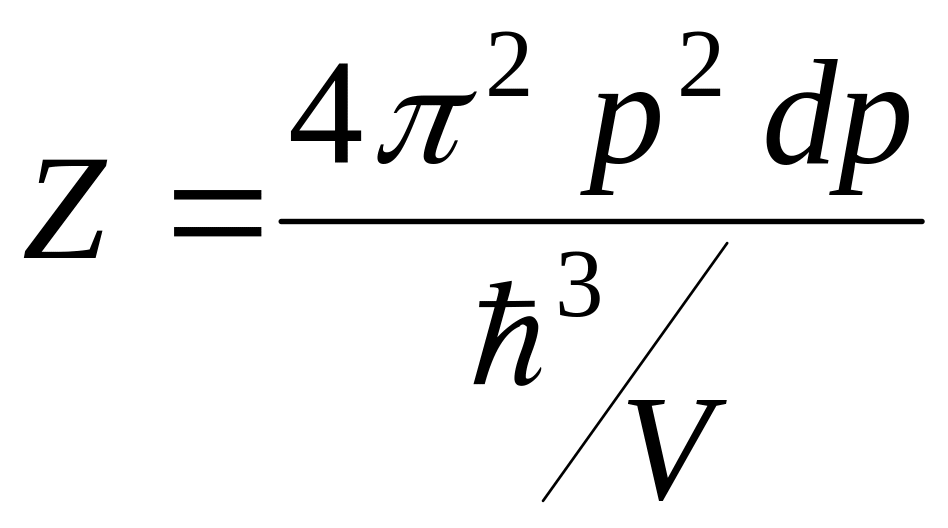С
учетом соответствующих преобразований
,
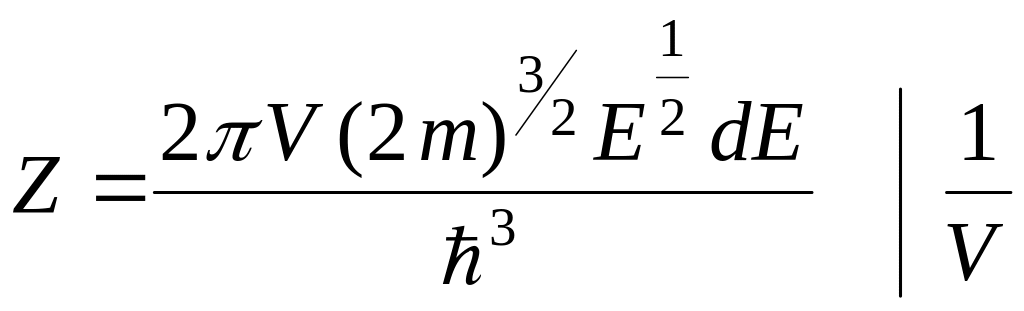а
число ячеек в единице объема есть
.
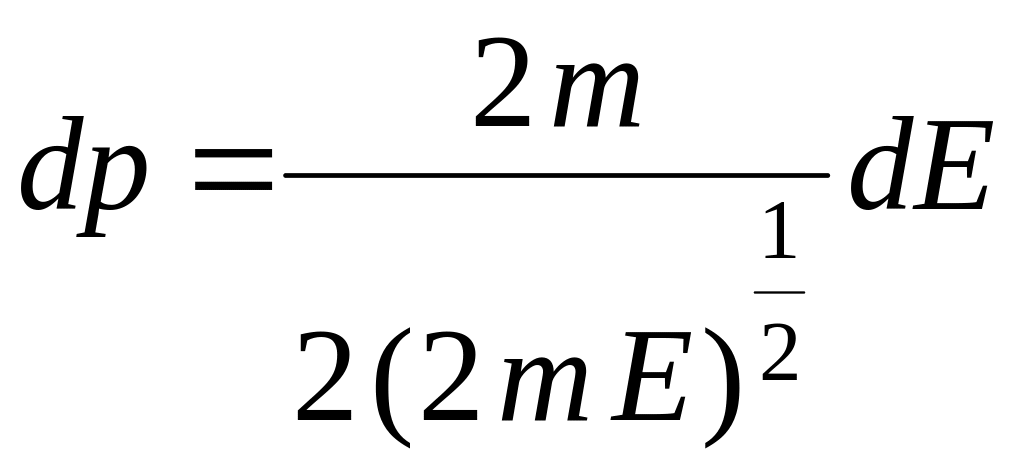
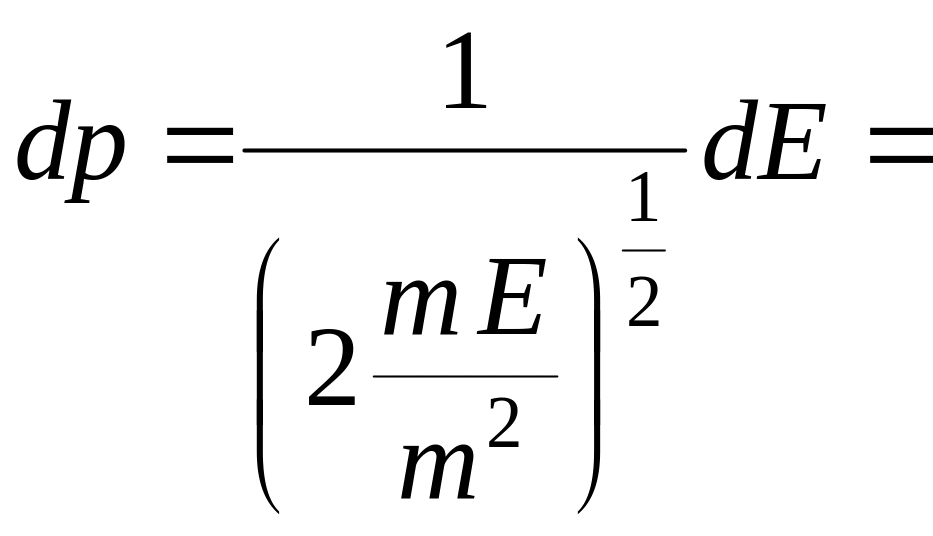
К
ак
и в предыдущем случае (распределение
электронов по составляющим импульса).
.
Анализ:
1
)
Зависимость
приведена на рисунке. Площадь
заштрихованной полоски соответствует
числу ячеек (квантовых сос -
тояний), находящихся в интер-
вале
.
2
)
Из рисунка следует, что с увеличением
площадь полосок увеличивается. Это
означает, что в равных по величине
интервалах
тем больше
,
чем выше
,
соответствующая этим ячейкам. Иначе
говоря, энергетические уров-
ни, соответствующие квантовым состояниям, располагаются тем ближе друг к другу, чем выше энергия, отвечающая этим уровням.
3)
Формула
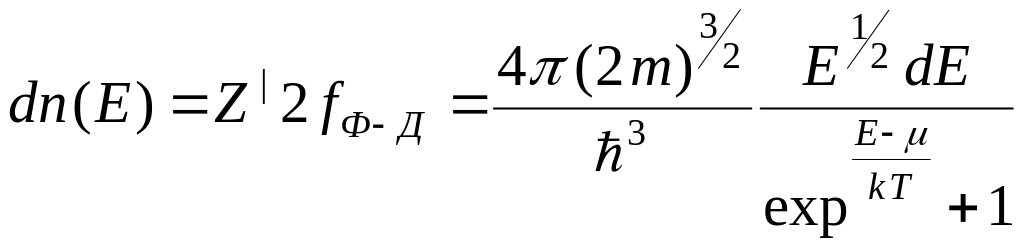- это закон распределения электронов
по энергиям.
Если
в полученный закон подставить выведенные
ранее соотношения, то выражение для
числа электронов в единице
объема
металла, полные импульсы которых
заключены в
интервале от p до p + dp, есть
.
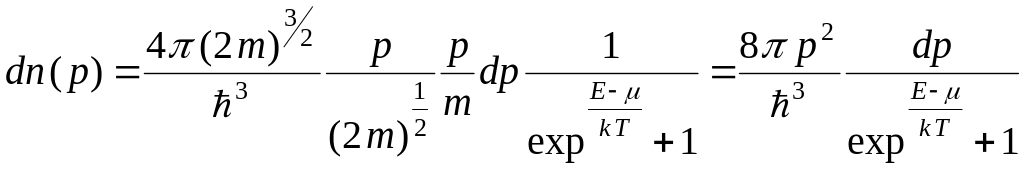