
Лекция 9. Элементы квантовой механики
Для объяснения свойств твердых тел и зависимости этих свойств от атомноэлектронной структуры вещества используются статистические и квантовомеханические представления.
9.1. Дуализм света. Формула л. Де - Бройля
В
явлениях интерференции, дифракции,
дисперсии, поляризации, поглощения и
рассеяния свет проявляет волновые
свойства (волновая теория, см. Лекции
1 - 5), т. е. свет - ЭМВ с
![]() и
и
![]() .
.
В
явлениях теплового излучения и фотоэффекта
(см. Лекции 6, 7) свет представляет собой
поток фотонов (корпускулярная теория)
с
![]() или
или
![]() и
и
![]() .
.
Таким образом, свет одновременно может проявлять как волновые, так и корпускулярные свойства (дуализм света).
Де - Бройль высказал гипотезу: "Дуализм свойственен и другим микрочастицам: электронам, протонам, в отдельных случаях атомам, ионам и т. д. - т. е. имеет универсальную природу".
Из гипотезы следует:
1) Дуализм присущ всем микрочастицам (МЧ), не только фотонам.
2)
Если существует микрочастица с
![]() и
и
![]() ,
то ей соответствует волна с
,
то ей соответствует волна с
![]() ,
которая называется волной де-Бройля.
,
которая называется волной де-Бройля.
3)
Соотношения
![]() - называются
соотношениями де - Бройля.
- называются
соотношениями де - Бройля.
4) Волны де - Бройля имеют квантовую природу, т. е. вероятностное, статистическое толкование и не имеют аналогов в классической механике.
5)
К. Девидссон и Л. Джермер наблюдали
дифракцию электронов от Ni
- пластины
и подтвердили, что как и для рентгеновских
лучей (см. Лекция 3), для электронов
справедлива формула Вульфа – Бреггов,
т. е.
![]() .
.
6) Т. Томпсон и Л.В. Тартаковский, изучая спектры электронов и рентгеновских лучей, показали их идентичность, т. е. сделали вывод, что электрон обладает волновыми свойствами.
7) О. Штерн наблюдал дифракцию у атомных и молекулярных пучков. Полученные интерференционные картины оказались идентичны световым.
8) В.А. Фабрикант, Н.Г. Сушкин и Л.М. Биберман, изучая дифракцию электронов, установили, что даже отдельный электрон обладает волновыми свойствами.
Этими экспериментами было доказано, что микрочастицы сочетают в себе одновременно корпускулярные и волновые свойства (дуализм). Эти свойства, применительно к электронам, можно сформулировать следующим образом:
а) Электрон - это сложное материальное образование со структурой, зависящей от свойств окружающей среды и обладающий волновыми свойствами.
б) Корпускулярная природа электрона проявляется в том, что он действует как единое целое, не делясь на части.
Итак, качественным отличительным признаком всех микрочастиц является одновременное сочетание в них корпускулярных и волновых свойств, причем волновыми свойствами обладают не совокупность, а каждая из частиц в отдельности.
9.2. Уравнение Шредингера
Качественное отличие микрочастиц от материальных точек, используемых в классической физике, требует и нового подхода к описанию их движения. Так как микрочастица обладает волновыми свойствами, то закон ее движения должен определяться законом распространения соответствующих волн, т. е. волн де - Бройля, и удовлетворять, как и в классической механике, волновому уравнению.
Приведем формальный вывод такого уравнения.
Пусть
плоская волна
![]() распространяется
вдоль
распространяется
вдоль
![]() (плоский
случай). Подбором времени
пусть 0
= 0, тогда
в
(плоский
случай). Подбором времени
пусть 0
= 0, тогда
в
к омплексной
форме
омплексной
форме
![]()
![]() .
.
![]()
Перейдем
к новой функции
![]() ,
,
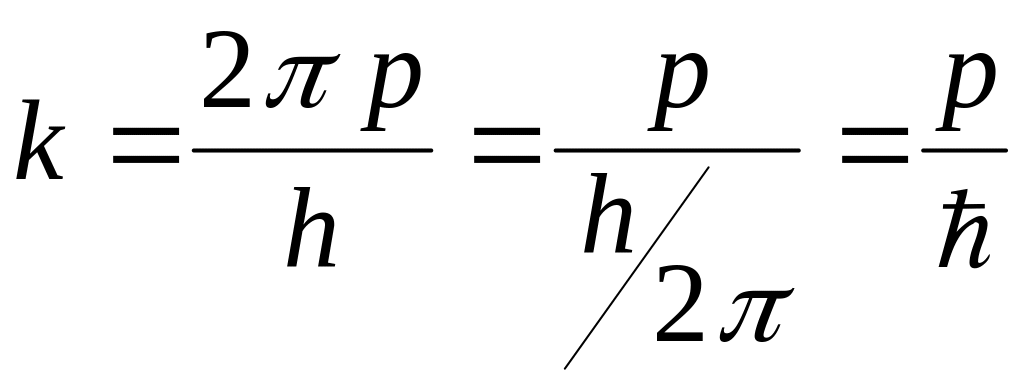
которая
связана с волной де - Бройля
![]()
![]()
![]()
и
воспользуемся соотношением
![]() где
где
![]() - кинетическая энергия,
- импульс микрочастицы.
- кинетическая энергия,
- импульс микрочастицы.
![]()
![]()
Таким образом,
![]()
 или
с учетом
или
с учетом
![]()
![]()
![]() ,
,
окончательно
![]() .
.
Анализ:
1) Как и в классической механике (см. "Механика . . .". Лекция 7) это дифференциальное уравнение 2-го порядка - есть волновое уравнение.
2) Полученное выражение в квантовой механике называется уравнением Шредингера.
3)
Если микрочастица движется в пространстве
(![]() ),
то
),
то
![]() ,
где
- оператор Лапласа.
,
где
- оператор Лапласа.
4)
Если микрочастица движется в силовом
поле, т. е. обладает потенциальной
энергией
![]() ,
тогда
,
тогда
![]()
![]() ,
а волновое
уравнение имеет вид:
,
а волновое
уравнение имеет вид:
![]() .
.
Во
втором слагаемом -
![]() появляется
после домножения обеих частей полученного
тождества (см. вывод).
появляется
после домножения обеих частей полученного
тождества (см. вывод).
Или
![]() .
.
Полученное выражение называется полным уравнением Шредингера и описывает движение микрочастицы в силовом поле.
5)
Функция
![]() - являющаяся решением волнового уравнения,
называется волновой функцией. Вид ее
зависит от характера сил поля, в котором
движется микрочастица. Эта функция
комплексная, поэтому физический смысл
имеет произведение *,
где *
- комплексно сопряженная функция. В этом
случае *
- есть действительное число.
- являющаяся решением волнового уравнения,
называется волновой функцией. Вид ее
зависит от характера сил поля, в котором
движется микрочастица. Эта функция
комплексная, поэтому физический смысл
имеет произведение *,
где *
- комплексно сопряженная функция. В этом
случае *
- есть действительное число.
6)
Величина
![]()
![]() - это вероятность того, что микрочастица
в любой момент времени находится в
выделенном объеме
- это вероятность того, что микрочастица
в любой момент времени находится в
выделенном объеме
![]() .
Так как вероятность не может быть
величиной неоднозначной, бесконечной
или изменяющейся скачком, то функция
.
Так как вероятность не может быть
величиной неоднозначной, бесконечной
или изменяющейся скачком, то функция
![]() должна быть непрерывной, однозначной,
иметь любую производную и конечные
значения во всех точках пространства.
должна быть непрерывной, однозначной,
иметь любую производную и конечные
значения во всех точках пространства.
7)
Из 6)
![]() - это условие нормировки. Функция,
удовлетворяющая данному уравнению,
называется нормированной. С другой
стороны, физически данное выражение
(условие) означает достоверный факт
(вероятность равна единице), что
микрочастица находится действительно
в выделенном объеме.
- это условие нормировки. Функция,
удовлетворяющая данному уравнению,
называется нормированной. С другой
стороны, физически данное выражение
(условие) означает достоверный факт
(вероятность равна единице), что
микрочастица находится действительно
в выделенном объеме.
8) Уравнение Шредингера можно записать и в виде

![]() После
замены
После
замены
9) Уравнение Шредингера в квантовой механике и
играет ту же роль, что и уравнение второго за - соответствую -
кона Ньютона в классической, т. е. – это урав - щего домноже-
нение движения микрочастицы. Таким образом, ния левой части
задать
закон движения микрочастицы означает
на
![]()
задать волновую функцию в любой момент времени и в любой точке пространства.
