
Лекция 2. Дифракция света
Явление дифракции состоит в том, что световые волны как бы "огибают" непрозрачные препятствия, проникая в область геометрической тени, т.е. нарушаются законы геометрической оптики, причем явление наблюдается при условии, что размер препятствия (это справедливо для малых отверстий или щелей) соизмерим с .
2.1. Принцип Гюйгенса – Френеля
П усть
на препятствие с двумя щелями падает
плоская волна с интенсивностью I0.
Принцип Гюй-
усть
на препятствие с двумя щелями падает
плоская волна с интенсивностью I0.
Принцип Гюй-
генса: "Каждая точка до которой доходит волновой фронт служит источником вторичных волн, которые в однородной изотропной
с реде
будут сферическими. Оги- Из теории
колебаний (см. "Ме -
реде
будут сферическими. Оги- Из теории
колебаний (см. "Ме -
бающая АВ вторичных волн (при ханика . . . ". Лекция 7) геометри-
t = const) и проникает в область ческое место точек, колеблю –
геометрической тени". Дополне - щихся в одной фазе, называется
ние Френеля: "Вторичные вол - волновой поверхностью. Для
ны являются когерентными и в плоской волны - это система па-
результате суперпозиции интер - раллельных плоскостей (прямых),
ферируют". В данном случае сферической – система сфер ( ок -
плоскость щелей совпадает с ружностей). Одна из волновых по-
с фронтом падающей волны. На верхностей (t = const), разделяю –
рисунке изображена только часть щая пространство на две части, в
волновых поверхностей вторич- которых есть и нет колебаний – на-
ных сферических волн, распро - зывается фронтом волны.
страняющихся в направлении
(показано стрелками) экрана.
П усть
S
– одна из
волновых поверхностей вторичной волны,
тогда в произвольной т. Р результирующее
колебание описывается уравнением
усть
S
– одна из
волновых поверхностей вторичной волны,
тогда в произвольной т. Р результирующее
колебание описывается уравнением
![]() где
А0
- амплитуда колебания в том
месте,
где находится
dS,
(
t
+ 0)
- фаза
колебания там же, dS
- элементарная
площадка
волновой
поверхности
S,
k
- волновое
число, r
- расстояние
от dS
до
т. Р, К()
- коэффициент
пропорциональности, зависящий от
величины угла .
При
увеличении
величина
К()
-
уменьшается,
если
где
А0
- амплитуда колебания в том
месте,
где находится
dS,
(
t
+ 0)
- фаза
колебания там же, dS
- элементарная
площадка
волновой
поверхности
S,
k
- волновое
число, r
- расстояние
от dS
до
т. Р, К()
- коэффициент
пропорциональности, зависящий от
величины угла .
При
увеличении
величина
К()
-
уменьшается,
если
![]() то К()
0 (мал.).
то К()
0 (мал.).
Анализ.
а)
Приведенное соотношение можно
рассматривать как математическое
выражение принципа Гюйгенса – Френеля.
Подынтегральное выражение с точностью
до постоянной совпадает с уравнением
сферической волны.
![]()
б) При расчете амплитуды световых колебаний, возбуждаемых некоторым источником S0 в произвольной т. Р, этот источник можно заменить эквивалентной ему системой вторичных источников (участков dS), любой вспомогательной поверхности S, охватываемой S0 и не охватываемой т. Р.
в) Вторичные источники dS когерентны S0 и между собой, поэтому возбуждаемые ими вторичные волны интерферируют при наложении.
г)
Амплитуда колебаний, возбуждаемых в т.
Р вторичной волной (вторичным источником
dS),
есть
![]() где A0
– амплитуда
первичной волны в точках элемента dS.
где A0
– амплитуда
первичной волны в точках элемента dS.
д) Расчеты по полученному выражению достаточно сложны, кроме некоторых симметричных случаев.
2.2. Метод зон Френеля
 Дано:
Из источника (S)
в однородной
среде распростра –
Дано:
Из источника (S)
в однородной
среде распростра –
няется сферическая (вторичная) волна.
Найти: амплитуду (А) результирующего колебания в
т. Р от всей волновой поверх –
ности (см. рис.).
Т очки
S и
P
лежат на
прямой SP
и волновая
поверхность симметрична относительно
SP.
Для это -
очки
S и
P
лежат на
прямой SP
и волновая
поверхность симметрична относительно
SP.
Для это -
г о
случая Френель разбил волновую поверхность
на зоны (центральная – первая, всего -
m),
причем расстояние от края каждой зоны
до т. Р отличается на /2,
где
- длина волны в данной среде, т.е. расстояние
от края m
- зоны до
т. Р есть bm
= b
+ m
о
случая Френель разбил волновую поверхность
на зоны (центральная – первая, всего -
m),
причем расстояние от края каждой зоны
до т. Р отличается на /2,
где
- длина волны в данной среде, т.е. расстояние
от края m
- зоны до
т. Р есть bm
= b
+ m
![]() Здесь m
- номер
зоны. Такое разбиение приводит к тому,
что колебания от соответствующих точек
двух соседних зон (края зоны, середина
и т.д.) будут приходить в рассматриваемую
точку в противофазе (разные знаки), т.
е. отличаться на .
Здесь m
- номер
зоны. Такое разбиение приводит к тому,
что колебания от соответствующих точек
двух соседних зон (края зоны, середина
и т.д.) будут приходить в рассматриваемую
точку в противофазе (разные знаки), т.
е. отличаться на .
![]()
Вычислим
площадь зон.
При![]()
![]()
![]() (min)
(min)
Площадь сферического сегмента S = 2 R h, (заштрихован на рисунке), где R - радиус сферы, h - высота сегмента. В нашем случае Sm = 2 ahm . В этом сегменте находится m - зон, тогда площадь m - ой зоны S m = Sm – Sm-1. Здесь Sm-1 – площадь (m - 1) – ой зоны.
Вычислим величину hm.
![]()

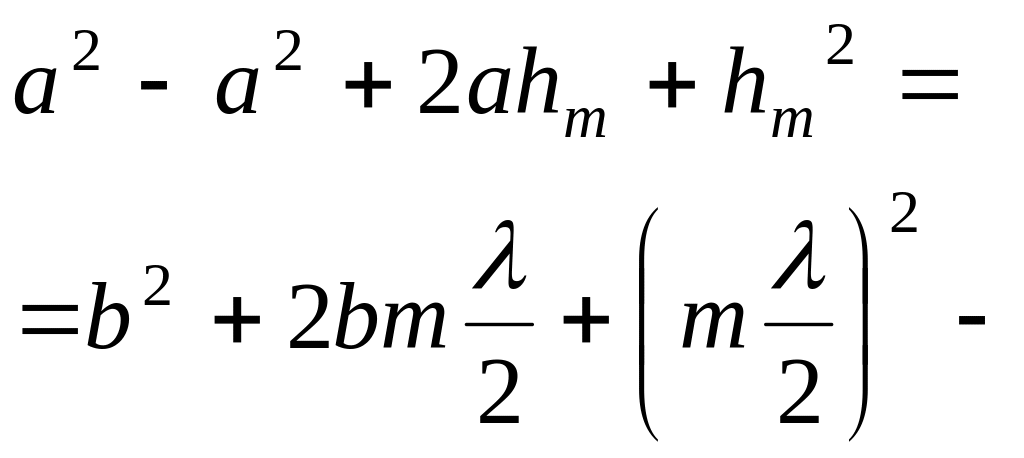
После преобразований:
2ahm
+ 2bhm
= bm
или 2hm(a
+ b)
= bm
.
![]()
Отсюда
- мало,
![]() - тем более,
- тем более,
![]() .
поэтому
.
поэтому
![]()
Определим: площадь сферического сегмента, содержащего m – зон, и площадь одной зоны.
![]()
![]()
Пусть
в сегменте, например, 6 - зон, тогда площадь
шестой зоны S
6
= S6
– S5.
Отсюда
![]() Итак, площадь m
- зоны равна
Итак, площадь m
- зоны равна
![]() ,
т.е. при небольших m
площади зон Френеля одинаковы, т.к. Sm
не зависит
от m.
,
т.е. при небольших m
площади зон Френеля одинаковы, т.к. Sm
не зависит
от m.
В ычислим
радиусы зон Френеля.
ычислим
радиусы зон Френеля.
При малых m (из рис.) hm << a, т.е. hm мало. SKN:
Тогда
h2m
0 и
![]() r2m
= a2
– (a
– hm)2
=
r2m
= a2
– (a
– hm)2
=
![]()
![]()
Итак,
радиусы зон Френеля изменяются как
корень квадратный из
m,
т.е. rm
![]() .
.
Результирующее
колебание в т. Р, согласно принципу
Гюйгенса – Френеля,
![]()
Проведем анализ:
1) bm = b + m , т.е. bm увеличивается с ростом m (числа зон). Формально bm соответствует величине r.
2) rm – радиус сегмента, который при увеличении числа m возрастает как rm . Формально rm – это A0.
3) С увеличением числа зон угол - возрастает, а K() - уменьшается.
4) Sm = const - площадь зон не зависит от m. Sm - это dS.
Все эти факторы приводят к тому, что амплитуды колебаний, возбуждаемые в т. Р соответствующими зонами Френеля, начиная с первой зоны, образуют монотонно убывающую последовательность
A1 > A2 > A3 > … > Am-1 > Am > Am+1,
причем амплитуды колебаний от двух соседних зон близки, а амплитуда Am – колебания (от m - зоны) в т. Р монотонно убывает при возрастании числа m. Кроме того, - от двух соседних зон равна , поэтому
Aрез = A1 - A2 + A3 –A4 + ………. .
Итак, амплитуда результирующего колебания может быть найдена алгебраически, причем амплитуды нечетных зон – положительны, четных – отрицательны.
Из полученного выражения следует:
1) Прямолинейное распространение света.
Результирующую амплитуду (Арез) можно представить в виде:
![]()
 .
.
![]()
С учетом уменьшающейся последовательности например,
![]() 9, 8, 7, 6, 5, 4, 3
9, 8, 7, 6, 5, 4, 3
т.е.
амплитуда результирующего колебания,
соз –
![]()
даваемая
в т. Р всей сферической волновой по –
![]()
верхностью,
равна половине амплитуды, одной
![]()
центральной
зоны. Или действие всей волновой
поверхности эквивалентно действию
половины центральной зоны. Кроме того,
свет распространяется прямолинейно в
пределах узкого канала (центральной
зоны):
![]() .
.
2) Если размер щели совпадает с площадью первой зоны, то

т. е. усиление интенсивности будет в 4 - раза.
3 )
Поскольку каждое колебание от
соответствующей зоны может быть
представлено в виде вектора, причем А1
А2
и 1
2,
то
)
Поскольку каждое колебание от
соответствующей зоны может быть
представлено в виде вектора, причем А1
А2
и 1
2,
то
![]() - есть вектор, соединяю -
- есть вектор, соединяю -
щий
концы
![]() и
и
![]() и сумма колебаний будет представлять
со -
и сумма колебаний будет представлять
со -
бой
спираль с характерными точками О, 1, С,
2. Фазы в т. О и т.1 отличаются на ,
то участок О1 – соответствует первой
зоне Френеля. Вектор
![]() -
это колебание 1 - ой зоны. Вектор
-
это колебание 1 - ой зоны. Вектор
![]() -
это колебание 2 - ой зоны, причем
и
- происходят в противофазе. Отсюда
-
это колебание 2 - ой зоны, причем
и
- происходят в противофазе. Отсюда
![]() - это результирующее колебание от всей
волновой поверхности. Полученное
выражение называется графическим
методом нахождения результирующей
амплитуды:
- это результирующее колебание от всей
волновой поверхности. Полученное
выражение называется графическим
методом нахождения результирующей
амплитуды:
![]() .
.
