
- •Кафедра «Теоретическая механика и Инженерная графика»
- •Часть 2
- •Москва 2009
- •Практическое занятие №2
- •Практическое занятие №3 Тени геометрических тел
- •2 Перспектива Практическое занятие №4
- •Расстояния от картины до прямой и между ними строим в перспективе по предыдущей задаче.
- •Дробные точки схода и отдаления
- •Практическое занятие №5
- •Построение квадрата в перспективе
- •Чтобы отложить в перспективе глубину точки а, надо от точки I на основании картины отложить отрезок I-3, взятый с проекции на предметную плоскость и равный I-a.
- •Построение сторон квадрата повторяет построение АпВп на рис.2.15
- •На рис.2.17 построен в перспективе прямоугольный параллелепипед. Построение повторяет элементы рис.2.15 и 2.16.
- •Практическое занятие №6
- •Практическое занятие №7
- •Начертательная геометрия и технический рисунок
Построение сторон квадрата повторяет построение АпВп на рис.2.15
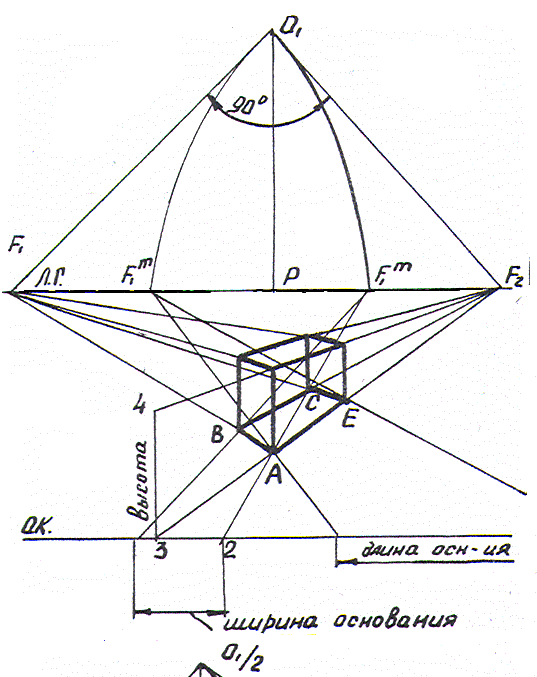
Рис.2.17
На рис.2.17 построен в перспективе прямоугольный параллелепипед. Построение повторяет элементы рис.2.15 и 2.16.
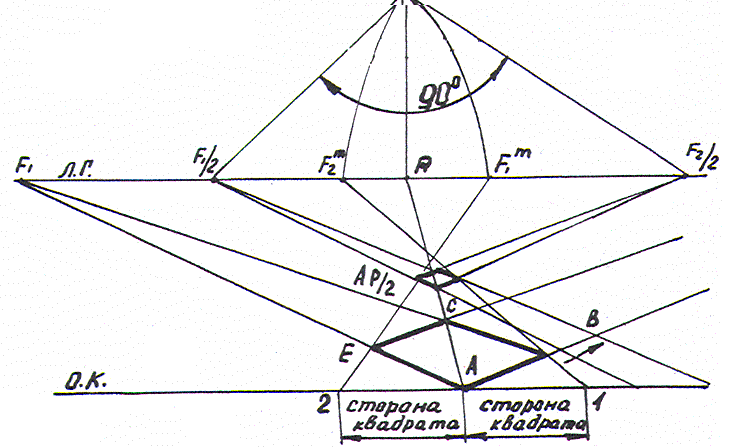
Рис.2.18
На рис.2.18 решена задача. Построен квадрат, расположенный в предметной плоскости в случайном положении, заданы вершина А на основании картины, длина стороны квадрата и направление стороны АВ в перспективе.
Точку
схода для стороны АВ определить нельзя,
она за пределами чертежа. Поэтому
возьмем половину расстояния от Р до
.
На стороне
![]() построим прямой угол и найдем
построим прямой угол и найдем
![]() .
Разделим пополам АР и из точки АР/2
проведем прямые в
.
Разделим пополам АР и из точки АР/2
проведем прямые в
![]() и
.
Получим направление сторон квадрата.
Чтобы отложить сторону квадрата на
полученных направлениях, надо
соединить точку I
с
и
.
Получим направление сторон квадрата.
Чтобы отложить сторону квадрата на
полученных направлениях, надо
соединить точку I
с
![]() и точку 2 с
и точку 2 с
![]() ,эти
прямые отсекут на
,эти
прямые отсекут на
![]() и на
и на
![]() точки, которые будут вершинами квадрата.
Но построенный квадрат удален от картины
в два раза дальше, чем надо было построить.
Из точки А проводим параллельные сторонам
построенного квадрата.
точки, которые будут вершинами квадрата.
Но построенный квадрат удален от картины
в два раза дальше, чем надо было построить.
Из точки А проводим параллельные сторонам
построенного квадрата.
На чертеже построена точка схода , чтобы убедиться, что построение проведено правильно.
Существует много методов построения перспективных изображений. С одним из них – методом перспективных масштабов мы познакомились (см. рис.2.14 и2.15). Наиболее распространенным является метод архитекторов. Разберем его суть.
Построение перспективы по методу архитекторов основано на нахождении картинных следов и точек схода прямых.

Рис.2.19
На рис.2.19 сделано построение перспективы квадрата методом архитекторов. В нижней части чертежа дана ортогональная проекция на предметную плоскость аппарата проецирования и квадрата. Плоскость картины, будучи предметной перпендикулярной плоскостью, проецируется в линию, совпадающую с основанием картины. На ортогональной проекции на предметную плоскость найдены картинные следы сторон квадрата: 4, 3, 2 и 1. В перспективе они будут на основании картины, так как квадрат лежит в предметной плоскости.
Точки схода находятся также на ортогональной проекции на предметную плоскость. Они получатся на линии горизонта в пространстве, а на ортогональном чертеже - на основании картины, куда проецируется вся картинная плоскость вместе с линией горизонта, в пересечении прямых, параллельных сторонам квадрата из 0.
На
перспективном чертеже
и
проецируются на линию горизонта. Теперь
из точек 4 и 3 проведем прямые в точку
схода
.
Например, точку А в перспективе можно
построить так. Картинный след 3 соединим
с
.
На ортогональной проекции проведен луч
зрения
![]() ,
который пересекает картину в точке 1
(случайно она совпала с картинным следом
стороны квадрата). Точку 1 проецируем
на
,
который пересекает картину в точке 1
(случайно она совпала с картинным следом
стороны квадрата). Точку 1 проецируем
на
![]() .
Это и будет перспектива точки А.
.
Это и будет перспектива точки А.
При построении перспективы квадрата с одной точкой схода можно построить вторую точку схода на совмещенной плоскости горизонта, исходя из перпендикулярности сторон квадрата.
На
стороне
![]() строится прямой угол, вторая сторона
которого определит вторую точку схода
.
строится прямой угол, вторая сторона
которого определит вторую точку схода
.
На рис.2.20 дано построение куба методом архитекторов.
При построении перспективы квадрата с одной точкой схода можно построить вторую точку схода на совмещенной плоскости горизонта, исходя из перпендикулярности сторон квадрата.
На стороне строится прямой угол, вторая сторона которого определит вторую точку схода .
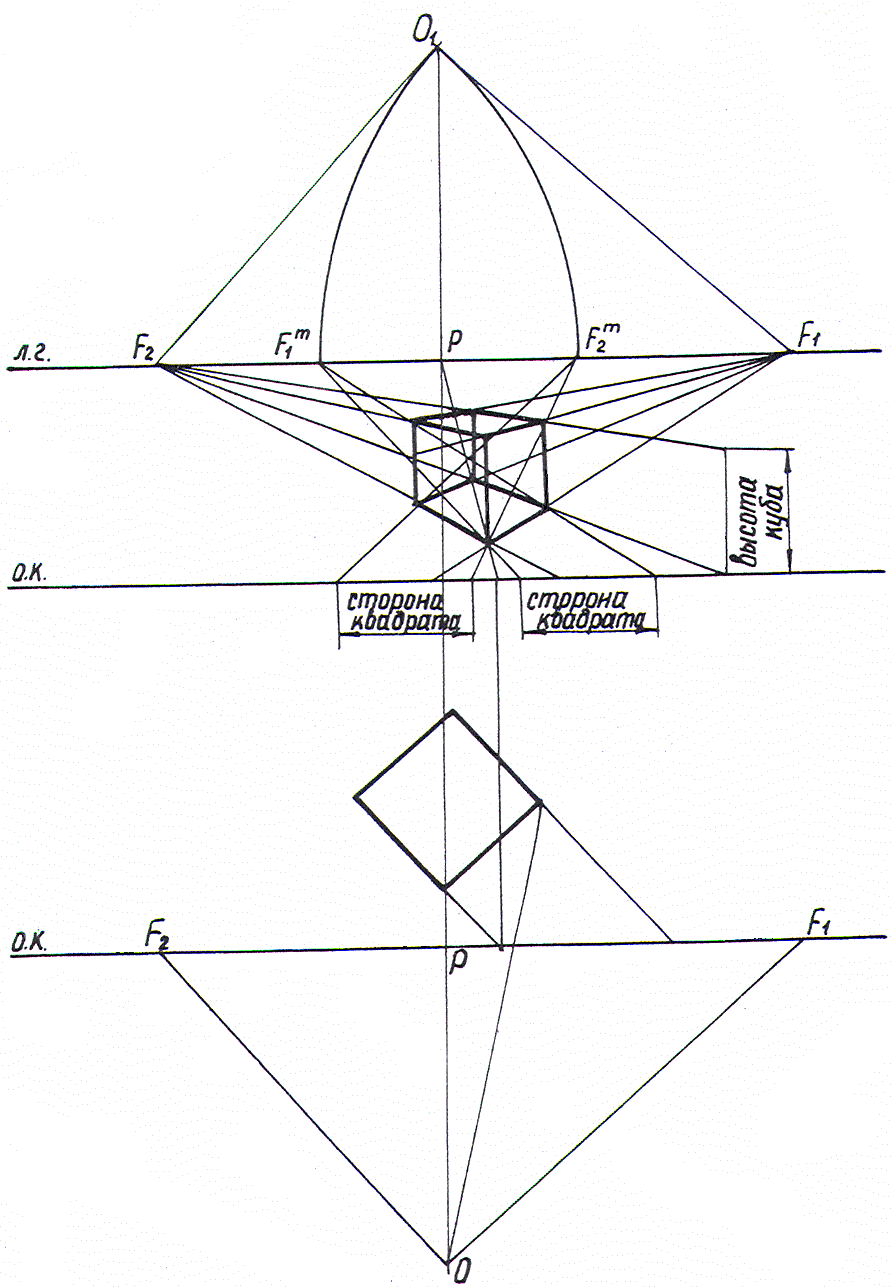
Рис.2.20
