Расстояния от картины до прямой и между ними строим в пер­спективе по предыдущей задаче.

Деление прямой на части: от точки Io перпендикулярно основа­нию картины откладываем длину отрезка и делим его на части. По­лученные точки соединяем с Р. Отрезок I_п2_п разделится в том же отношении.

3. Прямые I-2, 3-4 и 5-6 перпендикулярны к плоскости картины.

Строятся в перспективе следующим образом: на основании кар­тины откладываем расстояние I_o-3₀, 1₀-5₀ между прямыми 1-2, 3-4 и 5-6. Полученные точки 1₀, 3₀ и 5₀ соединим с Р. Это на­правление прямых в перспективе.

По образцу задачи I строим перспективу I_п-2_п и 3_п-4_п. Из точки 5₀ по перпендикуляру к основанию картины откладываем высоту прямой 5-6. Построенную длину отрезка 5-6 на 5₀-Р пере­носим на прямую 5_I-P. .

Деление прямой на части - см. второй чертеж таблицы.

4. Прямые I-2 и 3-4 горизонтальные и наклонные под углом 45⁰ к картине.

На чертеже такими являются диагонали верхней грани куба, которые строятся в перспективе так. Отложим от линии горизон­та в обе стороны от Р расстояние зрителя от картины, это бу­дут точки отдаления Д₁ и Д₂ - точки схода заданных прямых. Построим куб в перспективе так, чтобы его передняя грань сли­лась с картиной. По верхней грани проведены диагонали в точке схода I и 2. Деление такого отрезка на части производится как в задаче 3.

5. Прямые I-2 и 3-4 горизонтальные случайного положения.

Для определения точки схода прямой проведем прямую, парал­лельную направлению прямых I-2 и 3-4. Это прямая . На чер­теже она изображена на виде сверху на фоне плоскости П. Здесь плоскость картины слилась с её основанием. На предметной плоскости видно расположение данной прямой и луча О, параллель­ного направлению прямых. Здесь же получена точка I₀ - картин­ный след прямой I-2.

Точку I_o проецируем на основание картины, а - на линию горизонта. Соединив их, получаем направление прямой в перспективе.

Перспективы точек I и 2 можно найти или при помощи точки деления F^m , как это показано на следующем чертеже, или методом архитекторов. То есть на направление прямой в перспек­тиве I₀- надо спроецировать точки пересечения лучей зрения 0-I и 0-2 с картиной. Это точки I_I и 2_I. Перспективы их будут I_п и 2_п. Деление отрезка горизонтальной прямой случайного направления осуществляется при помощи точки деления , которая получа­ется на совмещенной плоскости горизонта с картиной на расстоя­нии 0_I - от по линии горизонта.

Допустим, надо разделить пополам I_п-2_п. Соединим точки I_п и 2_п с и на основании картины получим точки I₂ и 2₂. Это длина отрезка I-2. Разделив её пополам и соединив середи­ну с , получим середину на I_п-2_п.

6. Прямые I-2 и 3-4 общего положения.

Определим угол наклона заданной прямой к предметной плос­кости. Воспользуемся методом треугольника, т.е. на горизон­тальной проекции прямой I-2, приняв её за катет, построим треугольник A-I-2,- у которого А-2 является разностью высот от плоскости П точек I и 2. Искомый угол будет между гипоте­нузой A-I и её горизонтальной проекцией I-2.

Под найденным углом наклонен к предметной плоскости П луч зрения O , направленный параллельно прямым I-2 и 3-4. Если повернуть O до совмещения с картиной, то получим на картине прямую О_IF, наклоненную к основанию картины под углом . Эта прямая пересечет вертикаль, идущую из проекции точки на картинную плоскость, в точке схода в перспективе. Перенеся картинный след I₀ прямой I-2 на картинную плоскость, получим направление I₀- в перспективе этой прямой. Прое­цируя на плоскость картины точку пересечения луча зрения 0-2 с картиной с вида сверху на картинную плоскость, получим пер­спективу I_п-2_п.

Чтобы найти перспективу 3-4, надо построить перспективу точки 3 по координатам (глубина К-3 и расстояние от плоскости главного перпендикуляра К- f . На найденном направлении 3_п- находится точка 4_п аналогично точке 2_п.

Деление на части таких прямых в перспективе сводится к де­лению их на части в ортогональных проекциях и перенесению точек деления в перспективу.

Если представить, что на рис.2.3 даны параллельные прямой АВ, то нетрудно убедиться, что у них будет одна точка схода .

В таблице I на чертежах показаны параллельные прямые и их изображения :в перспективе. Они или имеют общую точку схода или совсем её не имеют.

Рис.2.6

Рис.2.7

Рис.2.8

Рис.2.9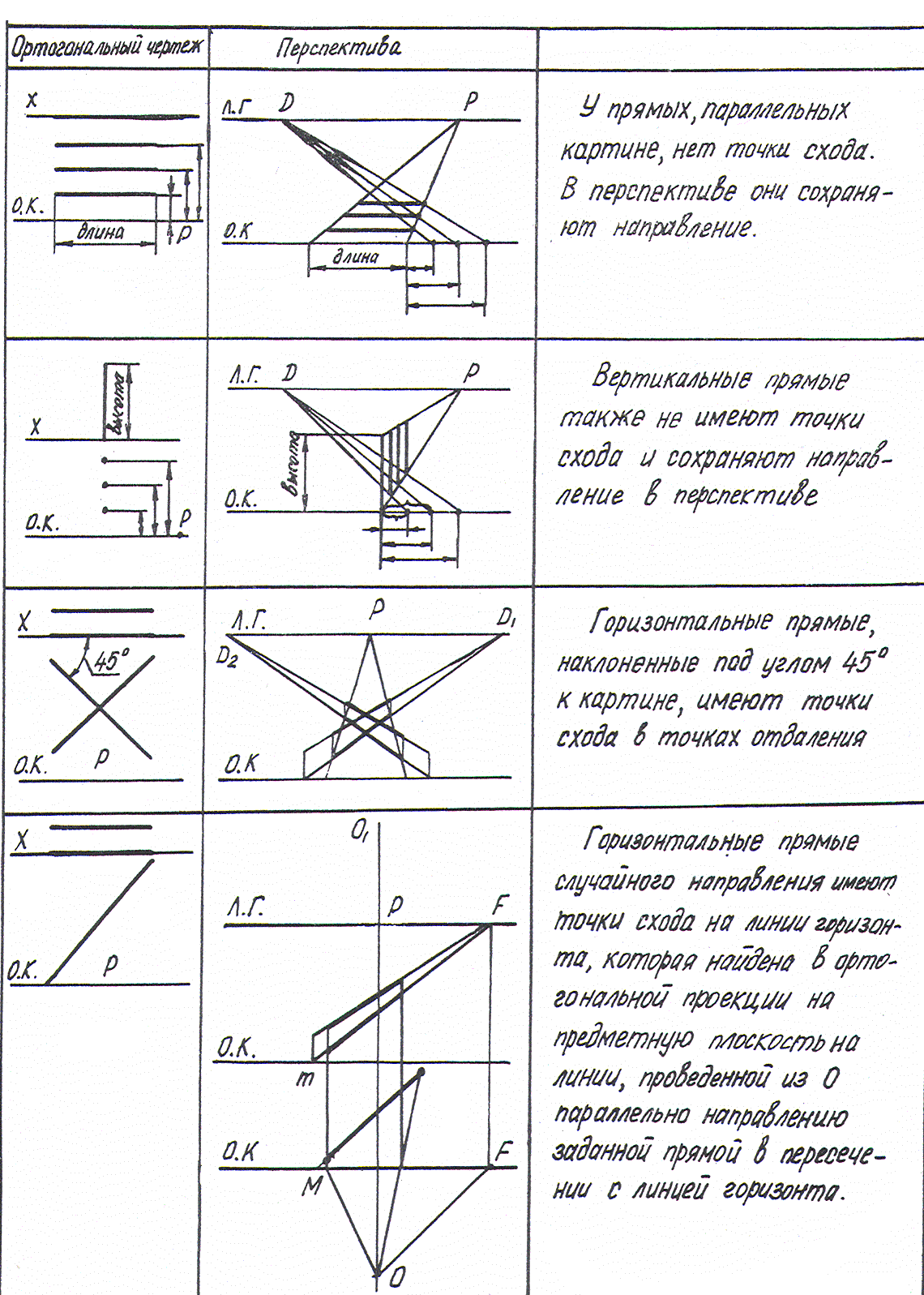

Перспективные изображения параллельных прямых даны на рис. 2.6-2.9 еще раз для справок при построении перспективных чертежей сооружений.

j

...

Перспектива пересекающихся прямых

Рис.2.10

На рис.2.10 изображены пересекающиеся горизонтальные прямые АВ и АС. Они перпендикулярны друг другу в пространстве. Пусть, на чертеже известно направление прямой АВ или им задаемся. Продлив АВ до пересечения с линией горизонта, получим точку схода . Чтобы найти точку схода , для второй стороны прямого угла АС, надо построить совмещенную с картиной плос­кость горизонта. На плоскость горизонта прямой угол между АВ и АС проецируется без искажения потому, что они заданы гори­зонтальными и лучи из точки зрения О будут направлены парал­лельно этим прямым. Совмещенную с картиной на плоскости гори­зонта точку зрения обозначим 0₁. Она расположится на перпендикуляре из Р к линии горизонта и отстоит от Р на расстоянии ОР, т.е. на расстоянии точки зрения от картины.

Соединим точки 0₁ с . На 0_{1 1} как на стороне построим прямой угол, вторая сторона которого пересечет линию горизон­та в точке . Соединив точку А с , получим перспективу прямого угла ВАС.

Если разделить угол при вершине 0₁ пополам на совмещенной плоскости горизонта, то можно провести биссектрису и в перспек­тиве. Для этого надо соединить А с I.

На рис.2.10 дано построение прямого угла и его биссект­рисы, когда вершина находится не в картинной плоскости. Углы наклона О_{1 1} и О_{2 2} к линии горизонта являются углами наклона прямых АB, КL и АС, LN к картине в пространстве.

Рис.2.11

На рис.2.11 построены в перспективе горизонтальные прямые АВ и АС, пересекающиеся в пространстве под углом 60⁰.