Лекция 6

Раздел II. Кинетика

Общие понятия и аксиомы кинетики. Простейшие действия с силами и системами сил.

Вопросы лекции.

1. Общие понятия кинетики.

2. Аксиомы (законы) динамики.

3. Силы и системы сил.

4. Аксиомы статики.

1. Общие понятия кинетики.

Кинетика — раздел теоретической механики, изучающий законы механического движения с учетом механического взаимодействия, т.е. причин, вызвавших данное механическое движение.

Другими словами, в кинетике даются ответы на вопросы: почему материальная точка движется по параболе; при каких условиях твёрдое тело будет совершать плоскопараллельное движение; при каких условиях твёрдое тело будет двигаться поступательно равномерно и прямолинейно, или оставаться в покое; и т.п.

Таким образом, в кинетике наряду с геометрическими свойствами механического движения, изученными в кинематике, учитываются и механические взаимодействия.

Напоминание: механическое взаимодействие – это такое взаимодействие, в результате которого изменяется механическое движение объекта. Количественной мерой механического взаимодействия является сила.

Сила – векторная величина, определяемая

1) модулем;

2) направлением;

3) точкой приложения;

4) линией действия.

Сила может быть представлена геометрически (на рисунке)

.

Силу (как и любой другой вектор) можно представлять аналитически. Для этого нужно выбрать три взаимно перпендикулярных единичных вектора

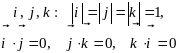
(предполагается, что их направления заданы, например, на юг, на восток и вверх, или каким-то иным способом). С этими единичными векторами обычно связывают координатные оси x, y, z соответственно, а введённые векторы задают положительные направления этих осей.

Тогда вектор силы определяется тройкой чисел

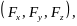11\* MERGEFORMAT ()

которые равны проекциям вектора силы не соответствующие оси (на направления единичных векторов ):

.

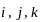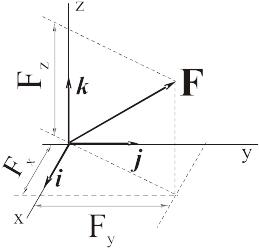Если в выражении (1) все три числа заданы, то модуль силы определится по формуле

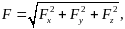22\* MERGEFORMAT ()

а направление найдётся с помощью направляющих косинусов: косинусов углов, которые образует вектор с положительными направлениями осей:

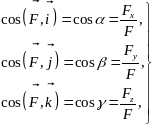33\* MERGEFORMAT ()

где F – модуль силы (2).

Замечания. 1) При аналитическом задании вектора силы точка её приложения указывается отдельно, например, с помощью координат 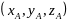, а вектор силы определяется равенствами (1) – (3), т.к. систему координат всегда можно параллельно перенести в любую точку.

2) Вектор силы вместо (1) можно записывать в виде

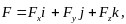44\* MERGEFORMAT ()

что часто используется на практике. Коэффициенты при единичных векторах в (4) – то же самое, что и в (1): проекции вектора на соответствующие оси.

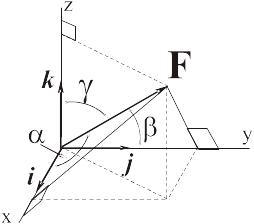
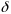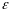3) Часто при задании вектора силы указывается угол между вектором силы и плоскостью Oxy, и угол между проекцией силы на плоскость Oxy и осью Ox.

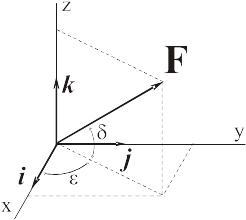
Тогда для определения проекций (1) сначала проектируем силу на плоскость Oxy

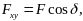
а затем на оси x и y:

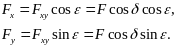
Проекция силы на ось z находится сразу:

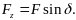
Сравнивая полученные выражения с равенствами (3) можем заключить, что

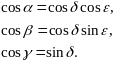
Остальные понятия кинетики ничем не отличаются от понятий, введённых ранее в кинематике:

физические объекты те же самые: материальная точка, механическая система и абсолютно твёрдое тело;

движение происходит в трёхмерном евклидовом пространстве с течением времени, причём ;

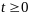все кинематические характеристики движения точек и твёрдых тел определяются методами кинематики;

связь – это любое ограничение на механическое движение.

Кинетику можно подразделить на две части: статику, изучающую правила действия с силами и законы частного случая механического движения – равновесия, и динамику, изучающую законы произвольного движения под действием произвольных сил.