
- •Решение
- •Получаем цепь с последовательным соединением резисторов r1-r234-r5.
- •Решение
- •Решение
- •Решение
- •Контурные уравнения для контуров:
- •Уравнение баланса мощностей
- •Баланс мощностей сошёлся, задача решена верно.
- •Решение
- •Решение
- •Решение
- •Решение
- •Из простых геометрических соображений очевидно:
- •Определим индуктивность l и емкость c рассматриваемой цепи по величинам заданных реактивных сопротивлений:
- •Р ешение
- •Решение
- •Амплитудное значение напряжения на ёмкости
- •Решение
- •Решение.
- •Решение.
Решение
Ёмкостное сопротивление xС
=![]() =
=![]() =
39,81 Ом.
=
39,81 Ом.
Амплитудное значение напряжения на ёмкости
uCm = Im xC = 1039,81 = 398,1 B.
Действующие значения
I
=![]() =
=![]() =
7,07 A,
uC
=
=
7,07 A,
uC
=![]() =
=![]() =
281,5 B.
=
281,5 B.
Действующие значения напряжений на активных сопротивлениях
ur1= I r1 = 7,0710 = 70,7 B, ur2= I r2 = 7,0720 = 141,4 B.
II-й закон Кирхгофа в векторной форме при одном токе I имеет вид ur1+ur2+uC = u, в соответствии с которым построена векторная диаграмма цепи (рис. б).
Из прямоугольного треугольника напряжений (наружный треугольник)
u
=![]() =
=![]() =
352 B,
=
352 B,
= arctg![]() =
arctg
=
arctg![]() =
-53.
=
-53.
Мгновенное значение напряжения сети
u(t)= Umsin(ωt+ψi+) = u sin(ωt+15+(-53)) = 352 sin(ωt – 38) B.
Напряжение на конденсаторе по фазе отстаёт от тока на 90, его мгновенное значение uC(t)= 398,1sin(ωt – 75) B.
Напряжение на участке r2-C, приложенное к ваттметру и вольтметру, рассчитаем по треугольнику напряжений u2-ur2-uC:
u2
= uW
=![]() =
=![]() =
315 B.
=
315 B.
Вольтметр схемы рис. 3.4,а измеряет действующее значение напряже-ния u2 = 315 B.
Показание ваттметра: PW
= uW
IW
cos![]() .
.
В нашем примере IW = I, поэтому
PW = u2Icos 2 = I(u2cos 2)= Iur2= IIr2 = I 2r2 = P2 – активная мощность, потребляемая сопротивлением r2, и P2 = 7,07220 = 1000 Bт.
ЗАДАЧА 18.
К цепи рис. подведено напряжение u = 220 В. До подключения ёмкости С приборы показывали: А I=2 А; W P=40 Вт. Требуется определить минимально возможное показание амперметра после подключения ёмкости, а также величину последней.
Р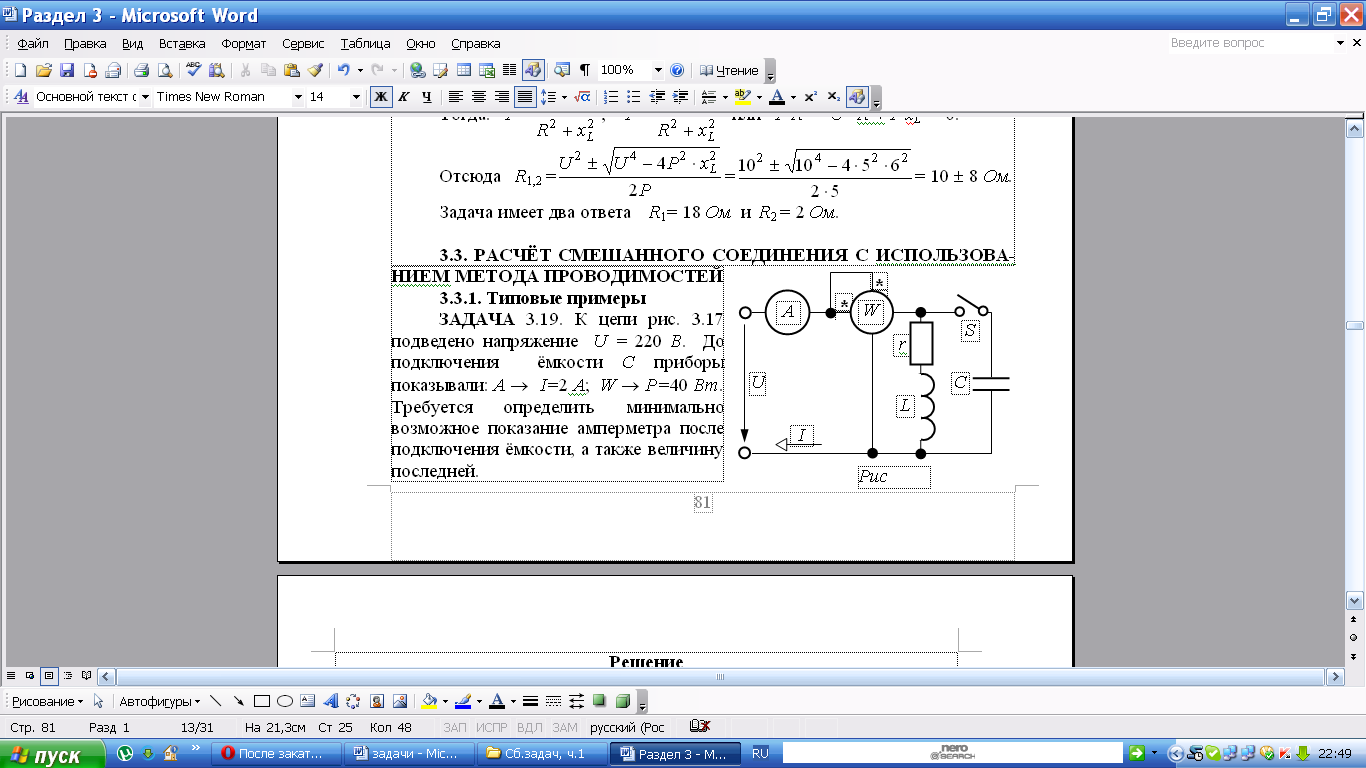 ешение
ешение
До подключения ёмкости, используя показания приборов, определяем полное, активное и индуктивное сопротивления ветви с r, L:
Z =![]() =
=![]() =
110 Ом; r
=
=
110 Ом; r
=![]() =
=![]() =
10 Ом;
=
10 Ом;
xL
=![]() =
=![]() =
109,5 Ом.
=
109,5 Ом.
Минимальное значение тока в неразветвлённой
части цепи будет иметь место при резонансе
токов в цепи после подключения ёмкости,
и в этом случае ток I
будет иметь только активную составляющую:
I = Ia
= Ug,
где g – активная
проводимость всей цепи, равная активной
проводимости ветви r,
L, а именно: g
=![]() =
=![]() =
2,2610 -4 См.
=
2,2610 -4 См.
Тогда I = Ug = 2202,2610 -4 = 0,182 А.
Величину ёмкости определим из условия, что её реактивная проводимость должна равняться реактивной проводимости ветви r, L, т.е.
С =![]() ,
откуда С =
,
откуда С =![]() =
=![]() =
2,8810 -5 Ф =
28,8 мкФ.
=
2,8810 -5 Ф =
28,8 мкФ.
ЗАДАЧА 19.
В схеме рис. определить действующее и мгновенное значение напряжения на ёмкости, если
u = 380 B; r = 1 кОм; С = 2 мкФ.
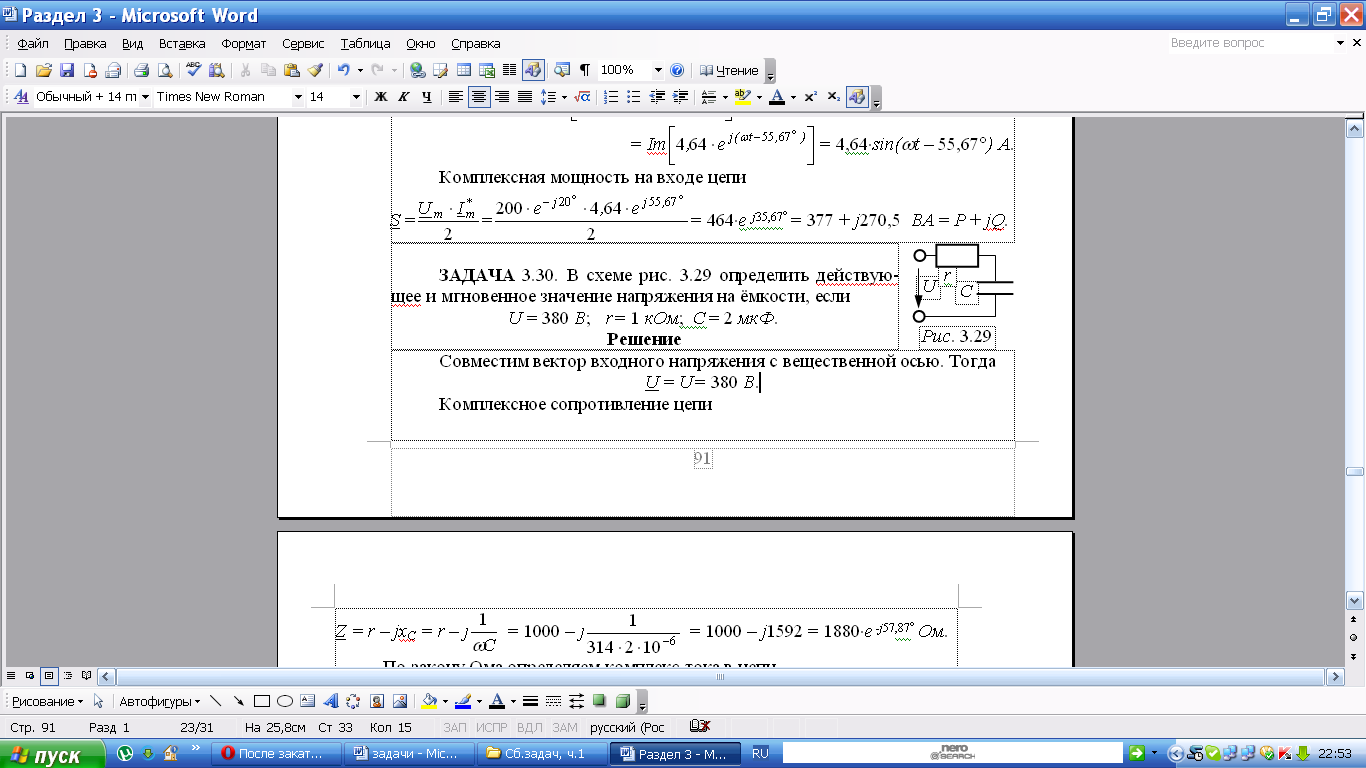
Решение
Совместим вектор входного напряжения с вещественной осью. Тогда
U = U = 380 B.
Комплексное сопротивление цепи
Z = r –
jхС = r –
j
= 1000 –
j![]() = 1000 –
j1592 = 1880e
-j57,87
Ом.
= 1000 –
j1592 = 1880e
-j57,87
Ом.
По закону Ома определяем комплекс тока в цепи
I =![]() =
=![]() =
0,202e
j57,87
А.
=
0,202e
j57,87
А.
Комплекс напряжения на ёмкости
UС = I(-jхС) = 0,202e j57,87(-j1592) = 321,8e –j32,13 В.
Мгновенное значение напряжения на ёмкости
uС(t)
= Im![]() =
455,1sin(t
– 32,13)
В.
=
455,1sin(t
– 32,13)
В.
Задача 20
Цепь переменного тока состоит из двух
параллельных ветвей. В первую ветвь
включены последовательно активное и
емкостное сопротивления:
![]() Ом,
Ом,
![]() Ом,
Ом,
![]() Ом. Вторая ветвь состоит из последовательно
соединенных активного и индуктивного
сопротивлений
Ом. Вторая ветвь состоит из последовательно
соединенных активного и индуктивного
сопротивлений
![]() Ом,
Ом,
![]() Ом. Напряжение на зажимах цепи
Ом. Напряжение на зажимах цепи
![]() В.
В.
Начертить схему цепи. Определить методом
комплексных чисел токи в параллельных
ветвях
![]() ,
,
![]() ,
и ток
,
и ток
![]() в неразветвленной части цепи: полную
в неразветвленной части цепи: полную
![]() ,
активную
,
активную
![]() и реактивную
и реактивную
![]() мощности всей цепи.
мощности всей цепи.

Д ано:
ано:
Ом;
Ом;
Ом
Ом;
Ом
В
Н айти:
айти:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
