Уравнение баланса мощностей

E₁×I₁ – E₅×I₅ + E₄×I₄ = I₁²×r₁ + I₂²×r₂ + I₃²×r₃ + I₄²×r₄ + I₅²×r₅ + I₆²×r₆,

120×21 – 6×8 + 80×8 = 21²×2 + 13²×6 + 16²×2 + 8²×6 + 8²×2 + 8²×3,

3112 Вт = 3112 Вт.

Баланс мощностей сошёлся, задача решена верно.

ЗАДАЧА 5

Параметры схемы рис. 1, заданы:

J₁ = 4 A, E₁ = 160 B, E₂ = 100 B, E₅ = 120 B, E₆ = 60 B,

r₁ = 50 Ом, r₃ = 40 Ом, r₄ = 60 Ом, r₅ = 30 Ом, r₆ = 20 Ом.

Р ассчитать схему Методом узловых потенциалов.

Решение

В приведенной задаче есть ветвь №2, сопротивление которой r₂ = 0, а проводимость g₂ = . Поэтому для узлов «1» и «4», которые являются конеч-ными точками ветви №2, узловые уравнения получаются вырожденными, из которых следует, что j ₄ – j ₁ = E₂.

Примем потенциал узла «1» j ₁ = 0, тогда j ₄ = E₂ = 100 B.

Для узлов с неизвестными потенциалами составляем систему узловых уравнений:

j ₂× – j ₃× – j ₄× = J₁ + ,

j ₃× – j ₂× – j ₄× = - – .

После подстановки чисел и переноса известных величин j ₄×r₃^-1 и j ₄×r₄^-1 в правые части уравнений системы получаем:

j ₂× – j ₃× = 4 + + , или j ₂×3 – j ₃×2 = 380,

j ₃× – j ₂× = - – + , -j ₂×3 + j ₃×6 = -320,

откуда j ₃ = 15 В, j ₂ = 136,7 В.

Токи ветвей схемы рис. 1.30 рассчитываем по закону Ома:

I₃ = = = 0,917 А,

I₄ = = = -1,417 А,

I₅ = = = 4,5 А,

I₆ = = = 3,085 А,

I₂ = = = – неопределённость, которая раскрывается с помощью I закона Кирхгофа, например, для узла «1»:

I₂ = I₅ – I₁ = 4,5 – 4 = 0,5 А.

ЗАДАЧА 6

Определить токи в ветвях схемы рис. 1, если E₁ = 16 В, J = 1 A, r₁ = r₂ = r₃ = r₄ = r₅ = 6 Ом.

Решение

1. Задаёмся положительными направлениями токов в ветвях цепи.

2. Полагаем, что в цепи действует только ЭДС E₁ (рис. 2) и определяем токи в ветвях:

I ₅=I₁= = =1 A.

Ток I₂ определим по формуле распределения тока в параллельные ветви

I ₂ = I₁ = 1 = 0,667 A.

Ток I₃ определим по I закону Кирхгофа

I₄ = I₃ = I₁ – I₂ = 1 – 0,667 = 0,333 A.

3. Теперь будем считать, что в цепи действует только источник тока J (рис. 3) и определим токи от действия этого источника.

Для определения токов в схеме рис. 3 преобразуем треугольник сопротивлений r₂-r₃-r₄ в эквивалентную звезду. Учтём, что сопротивления треугольника равны:

r ₂₃ = r₂₄ = r₃₄ = = = 2 Ом.

В результате преобразования получим эквивалентную схему рис. 4 откуда определим токи I₁ и I₅:

I₁ = J = 1 = 0,5 А,

I₅ = J – I₁ = 1 – 0,5 = 0,5 A.

Из схемы рис 3 с использованием II закона Кирхгофа для контура r₁-r₂-r₅ определим ток I₂:

r₁I₁ + r₂I₂ – r₅I₅ = 0, откуда I₂ = = 0.

По I закону Кирхгофа определим оставшиеся токи:

I₄ = I₂ + I₅ = 0,5 A, I₃ = I₁ – I₂ = 0,5 A.

4) По принципу наложения определим полные токи в ветвях

I₁ = I₁ + I₁ = 1 + 0,5 = 1,5 A, I₂ = -I₂ – I₂ = 0,667 A,

I₃ = I₃ + I₃ = 0,333 + 0,5 = 0,833 A,

I₄ = I₄ – I₄ = 0,333 – 0,5 = -0,167 A,

I₅ = I₅ – I₅ = 1 – 0,5 = 0,5 A.

ЗАДАЧА 7.

К коаксиальному кабелю приложено постоянное напря-жение U = 6 кВ. Длина кабеля l = 20 м (рис). Радиус жилы r₁ = 0,5 см, радиусы оболочки r₂ = 2 см, r₃ = 2,4 см. Относительная диэлектрическая проницаемость изоляции ε = 4.

Пренебрегая краевым эффектом определить емкость кабеля, построить графики Е(r), (r), найти запасенную в изоляции кабеля энергию.

Ответы: ёмкость кабеля по формуле С = = 3,21 нФ;

линейная плотность заряда  = = ;

напряжённость и потенциал

Е(r) = В/м, (r) = 4328ln В, где r[м];

графики Е(r) и (r) на рис.

О бъёмная плотность энергии в диэлектрике

w_Э = = .

Энергия поля, запасённая в кабеле

w_Э =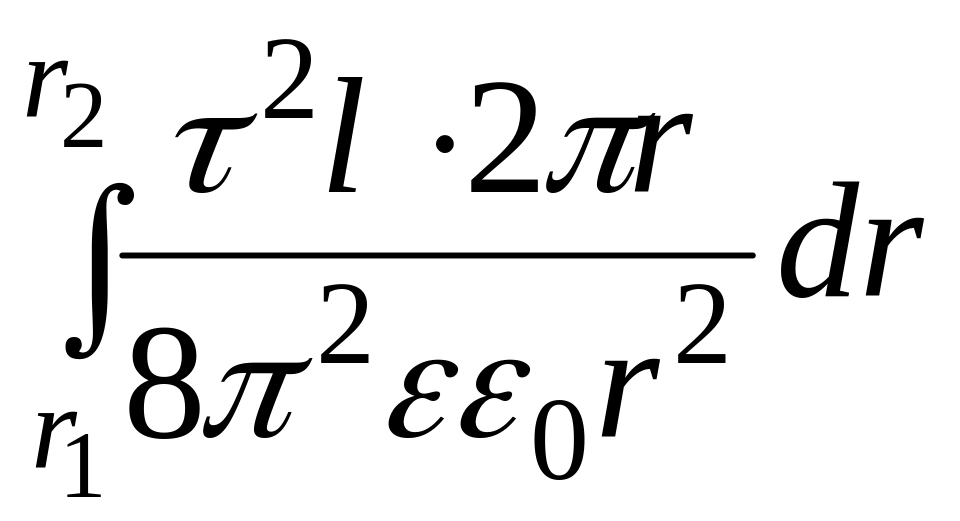 = ln = = 57,73·10 ^-9 Дж.

Задача 8

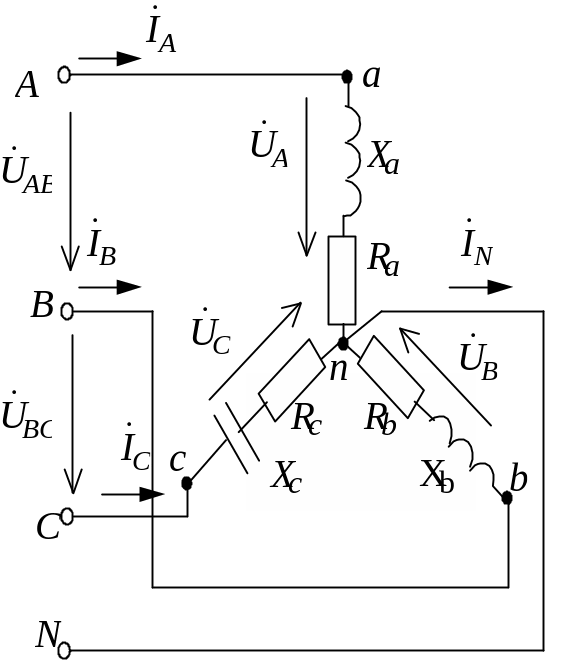
Трехфазный асинхронный двигатель включен в сеть 380 В по схеме «звезда». Параметры обмоток следующие: R_ф = 2 Ом, Х_ф = 8 Ом.

Требуется: изобразить схему включения двигателя в сеть; определить фазные и линейные токи; определить потребляемую активную мощность; построить векторную диаграмму токов и напряжений;

Р ешение:

Трехфазный асинхронный двигатель является симметричной активно-индуктивной нагрузкой, поэтому включается в сеть по схеме «звезда» без нейтрального провода. Его схема замещения представлена на рис. 1.3.8

Номинальное напряжение сети является линейным напряжением, т. е. , тогда фазное напряжение

Поскольку нагрузка симметричная, то расчет можно проводитьдля одной фазы.

Полное сопротивление фазы

Ф

А(а)

азный ток

.

Для схемы «звезда» линейный ток . Потребляемая активная мощность

г де  - фазовый угол,

.

Задача 9.

Три однофазных приемника включены в трехфазную сеть с напряжением 380 В по схеме “звезда с нейтральным проводом”. Сопротивления приемников: Ом; Ом; Ом.

Требуется изобразить схему включения приемников; определить токи в проводах сети; построить векторную диаграмму токов и напряжений; вычислить активную, реактивную и полную (кажущуюся) мощности.

Решение:

Схема включения приемников принципиальная и расчетная представлены на рис. 1, а,б.

а	б
Рис. 1

Наличие нейтрального провода обеспечивает симметричную систему фазных напряжений на приемниках. Напряжение сети – линейное напряжение

В.

Система фазных напряжений в комплексной форме

Сопротивления фаз

Для схемы “звезда“ фазные и линейные токи равны между собой и составляют

Ток в нейтральном проводе

При построении векторных диаграмм фазные и линейные напряжения и токи строятся относительно комплексных осей откладываются с учетом начальных фаз. Ток в нейтральном проводе – это результат геометрического сложения векторов фазных токов, и его расположение и длина должны соответствовать расчетному значению (рис. 2).

Рис. 2

Задача 10

В трехфазную сеть напряжением 380 В, частотой f = 50 Гц включен трехфазный асинхронный двигатель по схеме “треугольник“. Потребляемая активная мощность P = 1,44 кВт, коэффициент мощности cos = 0,85. Определить потребляемый двигателем ток, токи в обмотках двигателя, активное и индуктивное сопротивления, индуктивность катушек, полную и реактивную потребляемые мощности.

Решение:

Двигатель является симметричной нагрузкой, поэтому расчет ведем на фазу.

Сеть маркируется линейным напряжением, поэтому U_Л = 380 В.

При соединении по схеме “треугольник“ U_Л = U_Ф= 380 В.

Активная мощность, потребляемая нагрузкой,

отсюда фазный ток, протекающий в обмотках двигателя:

Потребляемые двигателем токи - линейные токи:

Полное сопротивление фазы обмотки двигателя:

Ом,

активное сопротивление

Ом,

индуктивное сопротивление

Ом.

Индуктивность обмотки определяется из выражения

,

Гн.

Полная потребляемая мощность:

кВА;

реактивная мощность:

ЗАДАЧА 11.

Рассчитать токи несимметричного треугольника (рис.а), построить векторную диаграмму, если

U = 380 В, r = x_C = 100 Ом, x_L = 100 Ом.

Н айти показания ваттметров, сравнить их с активной мощностью несимметричного трёхфазного приёмника.