4.7. Реализация оптимального регулятора.

Реализация оптимального закона управления (4.29) затрудняется наличием функциональных составляющих в его структуре. С целью упрощения реализации полученного закона найдем его изображение по Лапласу от всех составляющих

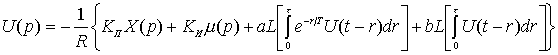(4.33)

где L[] - символ преобразования по Лапласу. Для нахождения изображений по Лапласу функциональных составляющих воспользуемся формулой свертки, согласно которой свертыванию оригиналов во временной области соответствует произведение их изображений

, (4.34)

Здесь знак - означает операцию свертывания оригиналов. В раскрытом виде формула свертки (4.34) записывается в виде

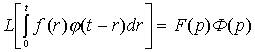. (4.35)

Сравнивая первый интеграл в выражении для оптимального закона управления (4.33) с интегралом в выражении (4.35) получим

и . (4.36)

Однако, в интеграле свертки и интегралах для функциональных составляющих закона (4.29) не совпадают верхние пределы интегрирования, поэтому прямо воспользоваться формулой свертки нельзя. Очевидно, что интеграл свертки необходимо привести к виду, обеспечивающему равенство

. (4.37)

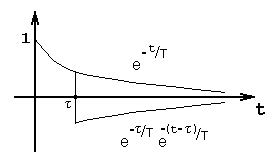Рис. 4.3.

Это можно достичь, если одну из функций в исходном интеграле искусственно сделать нулевой на интервале времени t> , т.е. при r> , что иллюстрируется рис.4.3. Функция, существующая на интервале и равная нулю вне этого интервала в соответствии с рис.4.3, имеет вид: . Тогда L - изображений от первой функциональной составляющей можно записать в виде

.

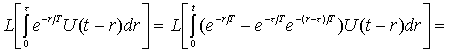
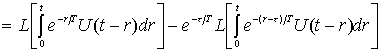Учитывая, что 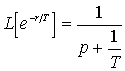и 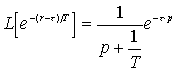, получим:

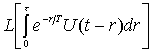
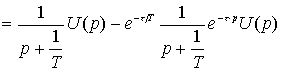. (4.38)

Аналогично найдем L-изображение для второй функциональной составляющей в выражении для оптимального закона управления

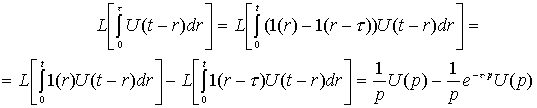. (4.39)

Исходя из полученных результатов, оптимальный закон управления примет вид(4.40). Знание операторной формы записи оптимального закона позволяет разработать структурную схему оптимального астатического регулятора для объекта первого порядка с запаздыванием (Рис.4.4).

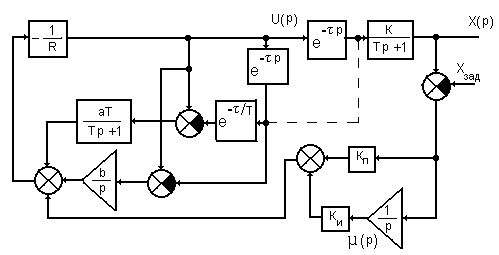
Рис.4.4. Структурная схема оптимальной системы управления.

Связь, обозначенная пунктиром, соответствует точному, теоретическому алгоритму управления (4.40). Однако на практике в объекте управления трудно выделить этот сигнал, поэтому его моделируют в регуляторе с помощью звена с чистым запаздыванием. Как видно из структурной схемы, оптимальный регулятор для объекта первого порядка с запаздыванием состоит из типового ПИ-регулятора и корректирующего устройства, в структуре которого содержится модель объекта управления. Данный регулятор особенно эффективен для управления объектами, в которых отношение /Т>0,5. На рис.4.5 приведены графики отработки единичного возмущающего воздействия в оптимальной системе управления объектом первого порядка.

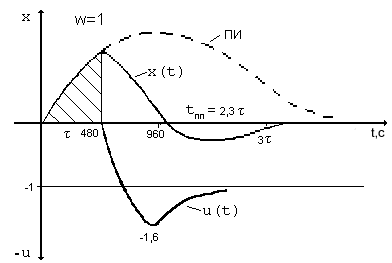Рис. 4.5. Переходный процесс в системе с оптимальным регулятором.

Параметры объекта управления были равны ; T=612сек; =480 сек. При этом коэффициенты закона (4.40) имели следующие значения ; ; ; , при R=1, . По аналогичной методике может быть получена структура оптимального регулятора для объекта второго порядка с запаздыванием. В этом случае оптимальный регулятор состоит из типового ПИД-регулятора и корректирующего устройства, в структуре которого содержится два инерционных звена и одно интегрирующее.