3. Цифровые регуляторы и их настройка

Цифровые алгоритмы управления являются важнейшей составной частью программного обеспечения микропроцессорных контроллеров и управляющих вычислительных машин (УВМ). УВМ осуществляет опрос сигналов с датчиков, вычисляет значения управляющих сигналов по заданному закону регулирования, а затем выдает их на исполнительные механизмы. Период опроса (квантования) изменяется в зависимости от динамических параметров процесса от долей до нескольких десятков секунд. В настоящее время наблюдается тенденция вытеснения аналоговых систем управления цифровыми . Объясняется это широкими возможностями по реализации самых совершенных алгоритмов регулирования, что, в свою очередь, гарантирует получение высокой точности и хорошего быстродействия в замкнутой системе непосредственного цифрового управления.

3.1. Алгоритмы цифрового пид регулирования

Наиболее распространенными алгоритмами являются ПИ и ПИД алгоритмы цифрового управления. При правильной настройке эти алгоритмы обеспечивают достаточно хорошее качество управления для большинства объектов промышленной технологии. Рассмотрим процедуру вывода алгоритма цифрового ПИД- регулятора из соответствующего непрерывного закона, имеющего вид

, (3.1)

где -ошибка регулирования.

Запишем уравнение (3.1) в конечных разностях, путем замены

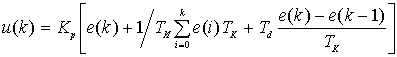, (3.2)

где =1,2,3...- номер периода квантования, - величина периода квантования.

Отметим, что при достаточно малых периодах квантования цифровой ПИД закон управления обеспечивает почти такое же качество процессов управления, что и исходный непрерывный закон (3.1).

На практике вместо вычислений абсолютных значений управляющего сигнала удобней вычислять его приращения на каждом такте. В этом случае становится возможным использовать этот алгоритм для управления объектами, оснащенными как пропорциональным так и интегрирующими исполнительными механизмами. В результате получаем так называемый скоростной алгоритм управления, полностью эквивалентный исходному

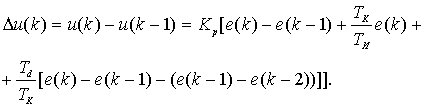(3.3)

Или, приведя подобные члены, получим

(3.4)

где обозначено

, (3.5)

Структурная схема цифрового ПИД регулятора приведена на рис. 3.1., где через обозначен блок задержки сигнала на один период квантования.

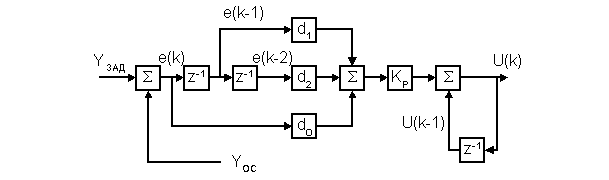Рис. 3.1. Структурная схема скоростного ПИД-регулятора.

Алгоритм работы всей системы управления при использовании цифровой модели объекта будет иметь вид

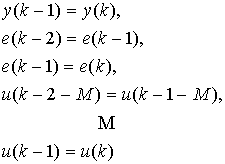
При этом параметры цифровой модели объекта управления в координатах "вход - выход" находятся путем взятия модифицированного Z-преобразования от передаточной функции объекта первого порядка с запаздыванием, что приводит к следующим формулам

, (3.6)

где , - целая часть отношения, - дробная часть.

3.2. Выбор периода квантования

Для того, чтобы эффект квантования по времени мало сказывался на динамику системы цифрового регулирования, рекомендуется выбирать период квантования из соотношения:

где: - это время достижения выходным сигналом уровня 95% от установившегося значения при подаче на вход объекта ступенчатого сигнала. Если объект первого порядка, то .

Другой подход к выбору величины периода квантования основан на рекомендациях американских ученых Зиглера и Никольса, согласно которым , где - период критических колебаний объекта управления. В реальных условиях при управлении инерционными процессами значение берется от 1 секунды до нескольких минут (в газоанализаторах, например, 1 раз в час). При регулировании малоинерционных процессов (например, расхода жидкости) величина может составлять десятые доли секунды. Нельзя выбирать большие периоды опроса, особенно для ответственных процессов, т.к. в этом случае аварийные ситуации будут ликвидироваться слишком медленно. В тоже время, при слишком малом периоде опроса повышаются требования к быстродействию ЭВМ и увеличивается влияние шумов.