
- •Гаврилов в.Л. Функции нескольких переменных
- •Евклидово -мерное пространство
- •Окрестности. Области
- •Функции нескольких переменных
- •Предел функции нескольких переменных
- •Непрерывность функции нескольких переменных
- •Решение задач
- •Вопросы для самопроверки по теме 8.1
- •Тесты для самопроверки по теме 8.1
- •Ответы на тесты по теме 8.1
- •8.2. Дифференцирование функций нескольких переменных
- •Частные производные
- •Дифференцируемость функции нескольких переменных
- •Полный дифференциал
- •Дифференцирование сложной функции одной переменной. Полная производная
- •Дифференцирование сложной функции нескольких переменных. Инвариантность формы полного дифференциала
- •Тогда функция
- •Дифференцирование неявных функций
- •В нашем случае
- •Частные производные высших порядков
- •Полные дифференциалы высших порядков
- •Рассмотрим функцию
- •Аналогично предыдущему можно показать, что
- •Решение задач
Дифференцирование сложной функции одной переменной. Полная производная
Определение. Функция нескольких переменных называется сложной, если сами аргументы - функции одной или нескольких переменных.
Пусть, например, - функция от переменных и , где
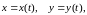
-
функции аргумента
 .
Тогда
сложная функция
.
Тогда
сложная функция
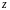 от
может быть
записана так:
от
может быть
записана так:
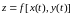
и продифференцирована как функция одной переменной.
Если
функция
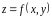 дифференцируемая в точке
дифференцируемая в точке
 ,
а функции
,
а функции
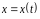 и
и
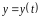 дифференцируемы при соответствующем
значении
,
то имеет место формула
дифференцируемы при соответствующем
значении
,
то имеет место формула
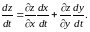 (8.14)
(8.14)
Пример.
Найти
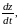 если
если
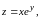 где
где
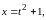 а
а

Решение. Находим
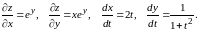
Подставляя найденные выражения в (8.14), получаем
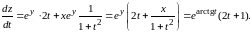
Аналогично
рассмотренному выше решается вопрос о
производной
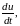 когда функция
задается
как дифференцируемая функция любого
числа переменных, каждая из которых, в
свою очередь, есть дифференцируемая
функция переменной
когда функция
задается
как дифференцируемая функция любого
числа переменных, каждая из которых, в
свою очередь, есть дифференцируемая
функция переменной
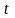 .
.
Так,
если
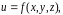 где
где
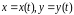 и
и
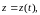 то
то
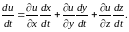 (8.15)
(8.15)
Рассмотрим
случай, когда независимая переменная
явно
входит
в выражение функции. Пусть
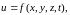
где
по-прежнему
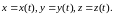
Распространяя
формулу (8.15) на случай функции четырех
аргументов
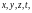 запишем
запишем
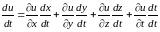
или
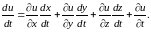 (8.16)
(8.16)
Производную
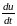 в формуле (8.16) называют полной
производной,
в
отличие от частной производной
в формуле (8.16) называют полной
производной,
в
отличие от частной производной
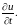
Пример.
Найти
частную производную
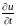 ,
и полную производную
функции
,
и полную производную
функции
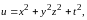 где
где
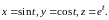
Решение.
Найдем сначала частную производную
считая
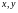 и
постоянными:
и
постоянными:
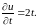
Так
как функция
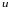 зависит от
зависит от
 как
непосредственно, так и через
как
непосредственно, так и через
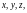 то для вычисления полной производной
воспользуемся
формулой (8.16).
то для вычисления полной производной
воспользуемся
формулой (8.16).
Находим
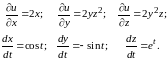
Подставляя в формулу (8.16), получаем
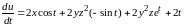
или
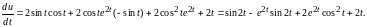
Дифференцирование сложной функции нескольких переменных. Инвариантность формы полного дифференциала
Пусть и

то
есть являются функциями двух переменных
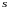 и
и
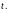
Тогда функция
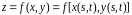
будет сложной функцией от и .
Если одной из переменных, скажем, , придается какое-либо постоянное значение, то становится функцией (сложной) только переменной , и ее производная по этой переменной (в данном случае, частная производная) вычисляется по формуле (8.14), но с заменой всех простых производных частными
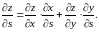 (8.17)
(8.17)
Так
же вычисляется частная производная
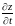
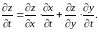 (8.18)
(8.18)
С помощью аналогичных рассуждений легко получить формулы для сложных функций произвольного числа переменных.
Дифференциал функции одной переменной обладает свойством инвариантности формы: она остается одной и той же вне зависимости от того, будет ли аргумент независимой переменной или некоторой дифференцируемой функцией другой переменной.
Это свойство инвариантности формы дифференциала, играющее важную роль в ряде вопросов математического анализа, справедливо и для функций нескольких переменных.
Дифференцирование неявных функций
Определение.
Функция
 аргумента
называется неявной,
если
она задана уравнением вида
аргумента
называется неявной,
если
она задана уравнением вида
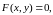
связывающим и , но не разрешенным относительно .
Однако
не всякое уравнение вида
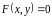 определяет неявную
функцию. Например, уравнение
определяет неявную
функцию. Например, уравнение
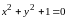 никакой функции
не определяет, так как
никакой функции
не определяет, так как
 для любых значений
и
.
для любых значений
и
.
Возникает
задача о нахождении условий, накладываемых
на функцию
двух переменных
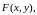 при которых уравнение определяет
неявную функцию
при которых уравнение определяет
неявную функцию
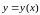 .
.
Достаточные условия существования, единственности и дифференцируемости неявной функции, заданной уравнением содержатся в следующей теореме.
Теорема.
Пусть
функция
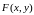 определена и непрерывна в
окрестности точки
определена и непрерывна в
окрестности точки
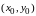 и имеет там непрерывные частные
производные
и имеет там непрерывные частные
производные
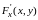 и
и
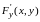 ,
причем
,
а
,
причем
,
а
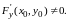
Тогда существует некоторая окрестность точки , в которой:
уравнение
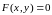 определяет единственную непрерывную
функцию
;
определяет единственную непрерывную
функцию
;при эта функция принимает значение
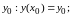
функция непрерывна и имеет непрерывную производную.
Геометрически
это означает, что существует окрестность
точки
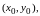 в которой кривая, заданная уравнением
представляет собой график непрерывной
и непрерывно-дифференцируемой функции
в которой кривая, заданная уравнением
представляет собой график непрерывной
и непрерывно-дифференцируемой функции
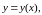 проходящий через точку
.
проходящий через точку
.
Производную при этом можно найти по формуле
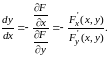 (8.19)
(8.19)
Пример.
Функция
задана уравнением
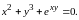 Найти
Найти

Решение.
В
условиях задачи уже предполагается,
что данное
уравнение определяет неявную
дифференцируемую функцию
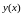 .
(Студент
самостоятельно может проверить выполнение
условий
приведенной выше теоремы, например в
окрестности точки
.
(Студент
самостоятельно может проверить выполнение
условий
приведенной выше теоремы, например в
окрестности точки
 ).
Остается только воспользоваться формулой
(8.19).
).
Остается только воспользоваться формулой
(8.19).
