Гаврилов в.Л. Функции нескольких переменных

При изучении данной темы Вам предстоит ознакомиться со следующими вопросами:

• Евклидово -мерное пространство.

• Окрестности. Области.

• Функции нескольких переменных.

• Предел функции нескольких переменных.

• Непрерывность функции нескольких переменных.

После изучения темы Вам следует ответить на вопросы для самопроверки и решить тесты. При возникновениии вопросов следует обратиться к [6], глава 1, с. 3-11.

Евклидово -мерное пространство

При изучении функций одной переменной было использовано взаимно- однозначное соответствие между множеством вещественных чисел и множеством точек числовой оси, что позволяло отождествить понятия «точка на числовой оси» и «вещественное число ». При введении прямоугольной системы координат на плоскости и в пространстве устанавливается взаимно-однозначное соответствие между множеством упорядоченных пар чисел и множеством точек плоскости, между множеством упорядоченных троек чисел и множеством точек трехмерного пространства. Это дает нам право говорить о паре чисел - как о точке плоскости и о тройке чисел - как о точке пространства.

По аналогии с предыдущим введем следующие определения.

Определение. Множество всевозможных упорядоченных систем вещественных чисел вида называется -мерным пространством (или пространством измерений), а каждая система чисел - точкой этого пространства.

Иногда это пространство называют арифметическим или координатным -мерным пространством.

Точку -мерного пространства будем обозначать одной буквой, например, а числа будем называть координатами точки.

Точку 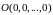назовем нулевой точкой пространства.

Расстояние между двумя точками и -мерного пространства определим с помощью формулы

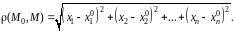(8.1)

При пространство измерений превращается соответственно в прямую, плоскость и обычное трехмерное пространство, а из равенства (8.1) при этих условиях получаются хорошо известные формулы для расстояний между двумя точками на прямой, плоскости и в трехмерном пространстве.

Определение. Пространство измерений, в котором расстояние между двумя точками определено формулой (8.1), называется - мерным евклидовым пространством и обозначается символом

Окрестности. Области

Пусть дана некоторая фиксированная точка и некоторое положительное число .

Определение. Множество точек пространства удаленных от точки меньше чем на , называется -окрестностью точки и обозначается

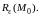
Т аким образом, если

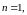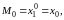
При т.е. в случае прямой, имеем и данное определение совпадает с введенным ранее для функции одной переменной: - множество точек прямой, удовлетворяющих условию то есть открытый промежуток длины с серединой в точке .

П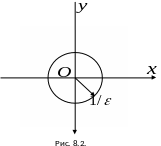 ри т.е. в случае плоскости, имеем - окрестность точки представляет множество точек плоскости , координаты которых удовлетворяют условию

или

Геометрически - это множество точек, лежащих внутри окружности радиуса с центром в точке (открытый круг) (рис. 8.1).

Для точки трехмерного пространства - это множество точек пространства, лежащих внутри сферы радиуса с центром в точке (открытый шар).

По аналогии, множество точек - мерного пространства для которых 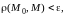называют - мерным открытым шаром с радиусом и центром в точке Для - мерного пространства - открытый шар.

Множество точек 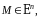для которых называют - мерным замкнутым шаром (иногда просто шаром) с радиусом и центром в точке .

Точки пространства определяемые упорядоченным набором вещественных чисел, называют конечными точками этого пространства. Кроме конечных точек в введем бесконечную точку, обозначив ее 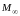или . Эту точку введем с помощью определения ее - окрестности.

Определение. Множество точек пространства , удаленных от нулевой точки более чем на , называется - окрестностью точки и обозначается

Точка если На прямой, то есть при - множество точек для которых и мы приходим к определению - окрестности точки на оси .

На плоскости 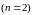условие принимает вид

или

то есть - окрестностью бесконечной точки на плоскости будет множество точек, лежащих вне окружности радиуса с центром в начале координат (рис.8.2).

В пространстве ( - множество точек пространства, лежащих вне сферы радиуса с центром в точке 0(0,0,0).

Понятие 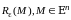используем для введения других определений.

Определение. Точка называется внутренней точкой множества если она принадлежит множеству вместе с некоторой своей - окрестностью.

Из определения следует, что, если внутренняя точка множества , то существует такое, что .

Определение. Точка называется граничной точкой множества если любая - окрестность точки содержит как точки принадлежащие, так и точки не принадлежащие .

Сама граничная точка может принадлежать или не принадлежать множеству .

Определение. Множество называется открытым, если все его точки являются внутренними.

Определение. Множество называется замкнутым, если оно содержит все свои внутренние и граничные точки; множество всех граничных точек множества называется его границей и обозначается .

Определение. Множество точек пространства , координаты которых заданы как непрерывные функции параметра называется непрерывной кривой в пространстве .

О пределение. Множество называется связным, если любые две точки этого множества можно соединить непрерывной кривой, целиком принадлежащей этому множеству.

Определение. Окрестностью точки называется любое открытое связное множество точек , содержащее саму точку .

Часто между и не делают различия, так как если существует , то она и является , если же существует , то всегда можно подобрать такое , что

Определение. Множество называется ограниченным, если существует - мерный шар 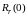радиуса с центром в нулевой точке 0(0,0,...,0) такой, что В противном случае множество называется неограниченным.

Определение. Множество 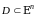называется открытой областью, если оно а) открытое и б) связное.

Определение. Замкнутой областью называется множество, которое получается в результате присоединения к открытой области всей ее границы:

Замечание. Часто применяют и более общий термин - область, понимая под этим и открытую, и замкнутую области, а также множество, получающееся в результате присоединения к открытой области части ее границы.

Приведем несколько примеров.

1. Рассмотрим множество точек плоскости координаты которых удовлетворяют условию Точки этого множества заполняют первый и третий квадранты плоскости , исключая оси координат (рис. 8.3). Это неограниченное открытое множество. Областью множество не будет, так как оно не является связным; действительно, точки и нельзя соединить непрерывной линией, целиком принадлежащей (начало координат множеству не принадлежит).

2. Пусть множество - множество точек, координаты которых удовлетворяют условию . Это ограниченная замкнутая область в пространстве .