Законы распределения нсв
Рассмотрим часто встречающиеся законы распределения НСВ: равномерный, показательный и нормальный.
2.3.1. Равномерное распределение
Непрерывная случайная величина , которая принимает значения только на отрезке a; b с постоянной плотностью распределения, называется распределенной по равномерному закону.
Таким образом, плотность распределения имеет вид:
.
График дифференциальной функции равномерного закона НСВ X имеет вид:
Интегральная функция распределения НСВ X, которая распределена по равномерному закону, имеет вид:
.
График интегральной функции равномерного закона НСВ X имеет вид:
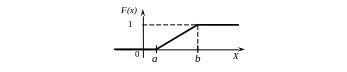
Математическое ожидание и дисперсия равномерной СВ:
.
Применение: Надо отметить, что равномерный закон распределения применяется при работе с округленными числами, измерение каких-либо величин по шкале измерительного прибора.
Пример 2.5. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляются до ближайшего деления. Определить закон распределения ошибки округления. Найти среднеквадратическую ошибку округления . Найти вероятность того, что при отсчете будет сделана ошибка менее 0,04.
Решение. Ошибку округления отсчета
можно рассматривать как случайную
величину
,
которая имеет равномерное распределение
в промежутке между соседними делениями.
Длина
длина промежутка,
в котором заключены все возможные
значения случайной величины
.
Плотность распределения вероятностей
данной случайной величины
имеет следующий вид:
.
Сначала найдем дисперсию равномерной СВ :
.
Используем формулу (2.11) и находим среднеквадратическую ошибку округления.
.
Ошибка отсчета будет менее 0,04, если
случайная величина заключена в интервале
или
.
Для нахождения вероятности события
заключающегося в
том, что при отсчете будет сделана ошибка
менее 0,04, воспользуемся формулой (2.5):
2.3.2. Показательное (экспоненциальное) распределение
Непрерывная случайная величина X, которая принимает только неотрицательные значения с плотностью распределения,
называется распределенной по показательному закону с параметром , где >0.
График дифференциальной функции показательного закона НСВ X имеет вид:
Интегральная функция распределения НСВ, распределенной по показательному закону, имеет вид:
График интегральной функции показательного закона НСВ X имеет вид:
Математическое ожидание и дисперсия показательно распределенной СВ X:
.
Применение: Надо отметить, что показательный закон распределения применяется в теории массового обслуживания; время ремонта, время простоя в очереди, время обслуживания.
Пример 2.6. Технический осмотр и обслуживание машин продолжается в среднем 2 часа. Составить закон распределения, если СВ X время техосмотра машины распределено по показательному закону. Найти среднее квадратическое отклонение. Найти вероятность того, что машина пройдет техосмотр менее чем на 1 час.
Решение. Среднее время техосмотра
равно 2 часа, а это
математическое ожидание
.
Значит, параметр
.
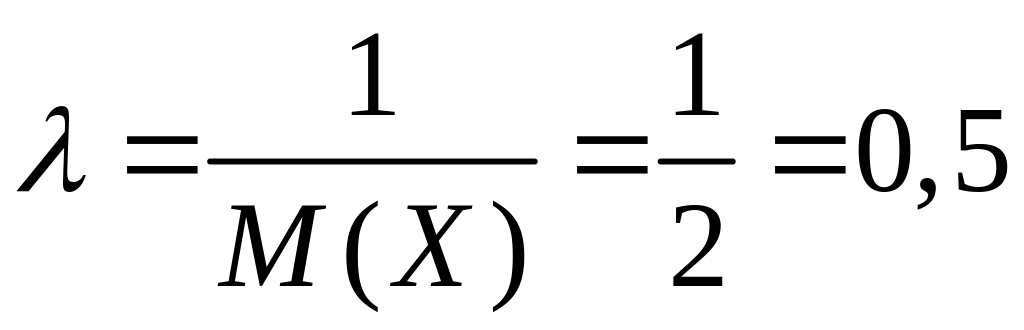Плотность распределения вероятностей
СВ X имеет следующий
вид:
.
Интегральная функция распределения СВ X имеет следующий вид:
.
Для показательного закона распределения
,
а
.
Следовательно
.
Чтобы найти вероятность того, что машина пройдет техосмотр менее чем на 1 час, воспользуемся формулой (2.1):
.