
- •Раздел 2
- •1. Дискретные одномерные
- •1.1. Закон распределения дсв. Функция распределения дсв
- •Свойства функции распределения
- •1.2. Числовые характеристики дсв
- •Свойства математического ожидания
- •Свойства дисперсии
- •1.3. Законы распределения дсв
- •Биноминальное распределение
- •Геометрическое распределение
- •Гипергеометрическое распределение
- •Закон Пуассона
- •2. Непрерывные одномерные
- •Интегральная и дифференциальная функции распределения нсв
- •Свойства интегральной функции нсв
- •Свойства дифференциальной функции нсв
- •Числовые характеристики нсв
- •Законы распределения нсв
- •2.3.1. Равномерное распределение
- •2.3.2. Показательное (экспоненциальное) распределение
- •2.3.3. Элементы теории надежности
- •2.3.4. Нормальное распределение
- •Свойства плотности вероятности нормального распределения
- •3. Моменты случайной величины
- •4. Закон больших чисел
- •5. Системы двух
- •Свойства интегральной функции распределения
- •Свойства дифференциальной функции распределения
3. Моменты случайной величины
Выше были рассмотрены числовые характеристики СВ: математическое ожидание, дисперсия и среднее квадратическое отклонение.
Рассмотрим ДСВ X, заданную законом распределения:

Найдем математическое ожидание X:
![]() .
.
Напишем закон распределения X 2:
 .
.
Найдем математическое ожидание X 2:
![]() .
.
Мы видим, что
![]() значительно больше
значительно больше
![]() .
Это объясняется тем, что после возведения
в квадрат возможное значение величины
X 2,
соответствующее значению x=100
величины X, стало равно
10000, т.е. значительно увеличилось;
вероятность же этого значения мала,
т.е. 0,01.
.
Это объясняется тем, что после возведения
в квадрат возможное значение величины
X 2,
соответствующее значению x=100
величины X, стало равно
10000, т.е. значительно увеличилось;
вероятность же этого значения мала,
т.е. 0,01.
Таким образом, переход от к позволил лучше учесть влияние на математическое ожидание того возможного значения, которое велико и имеет малую вероятность. Разумеется, если бы величина X имела несколько больших и маловероятных значений, то переход к величине X 2, а тем более к величинам X 3, X 4, и т.д., позволил бы еще больше «усилить роль» этих больших, но маловероятных возможных значений. Вот почему оказывается целесообразным рассматривать математическое ожидание целой положительной степени СВ (не только дискретной, но и непрерывной).
Определение 3.1. Начальным моментом
k-го порядка
СВ X называют
математическое ожидание величины
![]() :
:
![]() .
(3.1)
.
(3.1)
Для ДСВ X и НСВ X начальные моменты можно находить по следующим формулам:
 .
(3.2)
.
(3.2)
В частности,
![]() .
Пользуясь этими моментами формулу для
вычисления дисперсии можно записать
так:
.
Пользуясь этими моментами формулу для
вычисления дисперсии можно записать
так:
![]() .
.
Кроме моментов СВ X,
целесообразно рассматривать моменты
отклонения
![]() .
.
Определение 3.2. Центральным
моментом k-го
порядка СВ X
называют математическое ожидание
величины
![]() :
:
![]() .
(3.3)
.
(3.3)
Для ДСВ X и НСВ X центральные моменты можно находить по следующим формулам:
 .
(3.4)
.
(3.4)
В частности,
![]() .
В последнем соотношении видим, что можно
связать начальные и центральные моменты.
Нетрудно, исходя из определения
центрального момента и пользуясь
свойствами математического ожидания,
получить следующие формулы:
.
В последнем соотношении видим, что можно
связать начальные и центральные моменты.
Нетрудно, исходя из определения
центрального момента и пользуясь
свойствами математического ожидания,
получить следующие формулы:
![]() ,
,
![]() .
.
Моменты более высоких порядков применяются редко.
Пример 3.1. Дискретная случайная величина X задана законом распределения:
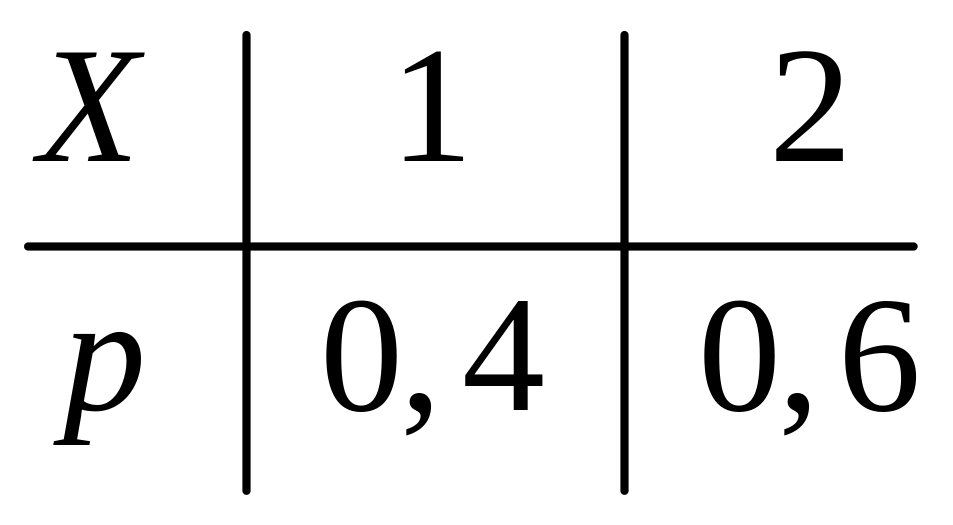 .
.
Найти начальные и центральные моменты первого, второго и третьего порядков СВX.
Решение. В соответствии с формулой (3.2) находим сначала начальные моменты:
![]() ;
;
![]() ;
;
![]() .
.
Вычислим центральные моменты, согласно формуле (3.4):
![]() ;
;
![]() ;
;
![]() .
.
Эмпирическим распределением называют распределение относительных частот. Такие распределения изучает математическая статистика. Теоретическим распределением называют распределение вероятностей. Такие распределения изучает теория вероятностей.
При изучении распределений, отличных от нормального, возникает необходимость количественно оценить это различие. С этой целью вводят специальные характеристики, в частности, ассиметрию и эксцесс. Для нормального распределения эти характеристики равны нулю. Поэтому, если ассиметрия и эксцесс изучаемого распределения имеют небольшие значения, отличные от нуля, то можно предположить близость этого распределения к нормальному. Большие же значения ассиметрии и эксцесса указывают на значительное отклонение от нормального.
Можно доказать, что для симметричного
распределения плотности вероятностей
(график такого распределения симметричен
относительно прямой
![]() )
каждый центральный момент нечетного
порядка равен нулю. Для несимметричных
распределений центральные моменты
нечетного порядка отличны от нуля. Любой
из этих моментов может служить для
оценки ассиметрии. Значение
)
каждый центральный момент нечетного
порядка равен нулю. Для несимметричных
распределений центральные моменты
нечетного порядка отличны от нуля. Любой
из этих моментов может служить для
оценки ассиметрии. Значение
![]() ,
следующим после него центральным
моментом нечетного порядка является
3.
,
следующим после него центральным
моментом нечетного порядка является
3.
Определение 3.3. Ассиметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:
 .
(3.5)
.
(3.5)
Графически это выглядит так:
Ассиметрия положительна, если «длинная часть» кривой распределения расположена справа от математического ожидания; ассиметрия отрицательна, если «длинная часть» кривой расположена слева от математического ожидания.
Практически определяют знак ассиметрии по расположению кривой относительно моды.
Для оценки «крутости», т.е. большего или меньшего подъема кривой теоретического распределения по сравнению с нормальной кривой, пользуются характеристикой - эксцессом. Четвертый центральный момент служит для характеристики крутости распределения X по сравнению с крутостью распределения нормальной СВ.
Определение 3.4. Эксцессом теоретического распределения называют характеристику, которая определяется равенством
![]() .
(3.6)
.
(3.6)
Для нормального распределения
![]() ,
поэтому
,
поэтому
![]() .
.
Графически это выглядит так:
Если эксцесс некоторого распределения отличается от нуля, то кривая этого распределения отличается от нормальной кривой: если эксцесс положительный, то кривая имеет более высокую и «острую» вершину, чем нормальная кривая; если эксцесс отрицательный, то сравниваемая кривая имеет более низкую и «плоскую» вершину, чем нормальная кривая.
