4. Рівняння Лагранжа іі роду.

Рівняння Лагранжа ІІ роду мають вигляд:

де - кінетична енергія матеріальної системи;

- узагальнена координата, узагальнена швидкість; - узагальнена активна сила, що відповідає цій узагальненій координаті.

У відповідності з тим, що визначенню підлягає прискорення , в якості узагальненої координати обираємо – вертикальне переміщення тіла 1. Інших узагальнених координат – немає, оскільки система має один ступінь вільності .

Згідно (4.1) визначимо кінетичну енергію системи через обрану узагальнену координату та узагальнену швидкість . Використовуючи (1.17) з урахуванням , отримаємо:

Для знаходження узагальненої активної сили надамо системі можливого переміщення та запишемо роботу активних сил на цьому переміщенні.

Скориставшись виразом (1.9), маємо:

Як відомо, коефіцієнт в виразі при є узагальнена активна сила. Отже:

(4.4)

Оскільки: а , підставляючи (4.4) та (4.2) в рівняння Лагранжа ІІ роду:

отримаємо результат, тотожній (1.23).

В разі необхідності знаходження наприклад , в якості узагальненої координати треба обирати кут повороту тіла 3 - (тоді узагальнена швидкість ).

5. Метод кінетостатики.

Інший спосіб вирішення вищезазначеної задачі пов'язаний з необхідністю складання диференціальних рівнянь руху кожного тіла окремо і подальшого вирішення цих рівнянь як системи.

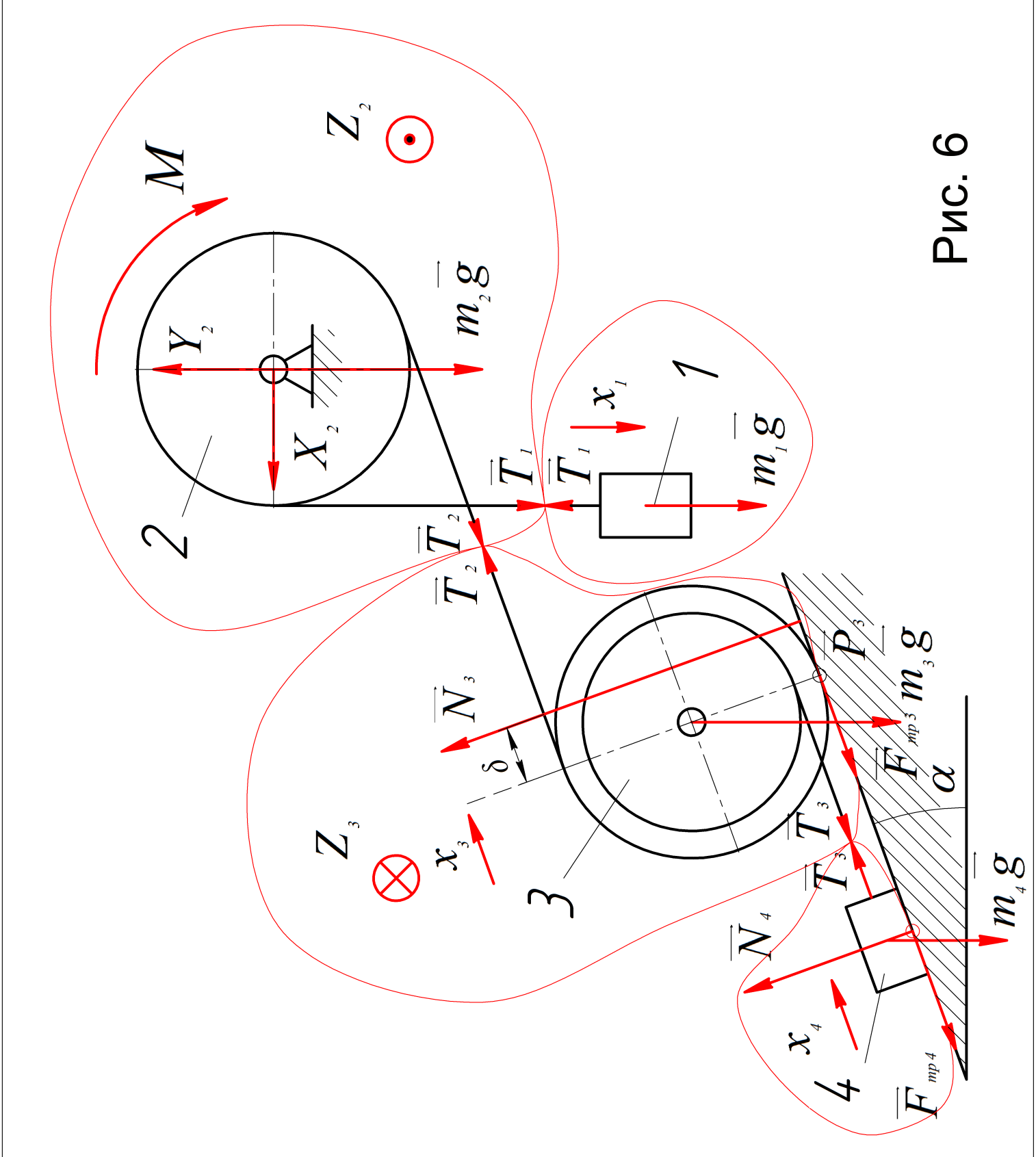
Кожне з тіл подумки укладемо в замкнутий об’єм (рис. 6). До зовнішніх сил в цьому випадку додаються також сили натягу ниток (i=1,2,3).

Дуже важливим питанням при вирішені задачі цим методом є правильний вибір напрямків вісей, в яких досліджуется рух тіл. Для кожного з тіл покажемо додатній напрямок вісей х, вздовж яких тіла рухаються поступально та прискорено (вісі ) і додатній напрямок вісей z, навколо яких тіла прискорено обертаються (вісі

Як відомо диференціальне рівняння поступального руху тіла записується як , а обертального - . Рівняння плоскопаралельного руху – сукупність двох вище наведених рівнянь.

Отже, рівняння поступального руху тіла 1 вздовж вісі х₁ має вигляд:

. (5.1)

Рівняння обертального руху диска 2 навколо вісі z₂ має вигляд:

. (5.2)

Рівняння плоскопаралельного руху тіла 3 складаєтся з рівняння поступального руху центру мас вздовж вісі х₃ та рівняння обертального руху навколо вісі z₃, що проходить через центр мас

, (5.3)

. (5.4)

Рівняння поступального руху тіла 4 вздовж вісі х₄ виглядає так:

. (5.5)

Розглядаючи рівняння (5.1-5.5) як систему рівнянь, з урахуванням , отримаємо:

(5.6)

Лінійні W_i та кутові ε_i прискорення пов’язані між собою. Їх взаємозв’язок можна отримати, взявши похідну за часом від співвідношень (1.16)

; ; ; . (5.7)

З урахуванням (5.7) систему (5.6) перепишемо у вигляді:

(5.8)

Система з п’яти рівнянь являє собою систему лінійних алгебраїчних рівнянь з п’ятьма невідомими – чотирма силами (T₁, T₂, T₃, T₄) та прискоренням W₁ поступального руху тіла 1.

Нескладно побачити, що виключаючи з третього та четвертого рівнянь системи (5.8) силу тертя F_тр3 , отримаємо рівняння

. (5.9)

З урахуванням того, що – момент інерції східчастого диску 3 відносно миттєвої вісі обертання, а кутове прискорення тіла 3, можна стверджувати, що (5.9) – рівняння обертального руху диску 3 навколо миттєвої вісі обертання.

Виключаючи з перших двох рівнянь (5.8) силу натягу отримаємо:

Вирішуючи спільно рівняння (5.9) та пяте рівняння системи з системи (5.8) з метою виключення сил натягу , маємо:

=

Виражаючи з (5.10) силу :

та підставляючи (5.12) в (5.11), з урахуванням ; отримаємо:

(5.13)

Поділяючи чисельник та знаменик (5.13) на 2 , отримаємо вираз для тотожний (1.23).

В разі необхідності знаходження будь-якого іншого кінематичного параметру, наприклад , треба в (2.7) всі інші параметри виразити через :

;

Тоді система рівнянь (5.6) буде мати вигляд:

(5.15) Вирішуючи систему рівнянь (5.15) відносно , отримаємо вираз тотожній (1.30).

Література

1. Решебник

2. Методичка Шальда

3. Ссылка на Кильчевского

25